7. Проверочный расчет быстроходного вала

7.1. Определение реакций опор

Для проверочного расчета статической и усталостной прочности ступенчатого вала (быстроходного или тихоходного в соответствии с заданием) составим его расчетную схему (см. рис. 13).

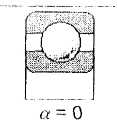
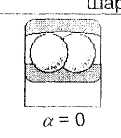
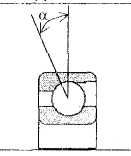
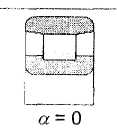
Поскольку подшипники прямозубой передачи, воспринимают только поперечные нагрузки, то заменим их шарнирными неподвижными опорами R_A и R_B. Причем положение шарнирной опоры определим с учетом угла контакта а подшипника качения, определяемого конструкцией подшипников (см. рис. 14) Поскольку для всех вариантов цилиндрических прямозубых редукторов (см. рис. 3-5) заданных исполнений a = 0, то для их радиальных подшипников положение опор принимаем в середине ширины подшипников.

Геометрические параметры вала определим на основании чертежа редуктора с межосевым расстоянием a_W = 200 мм (см. вариант 1) а = 125 мм; b = 75 мм; с = 75 мм.

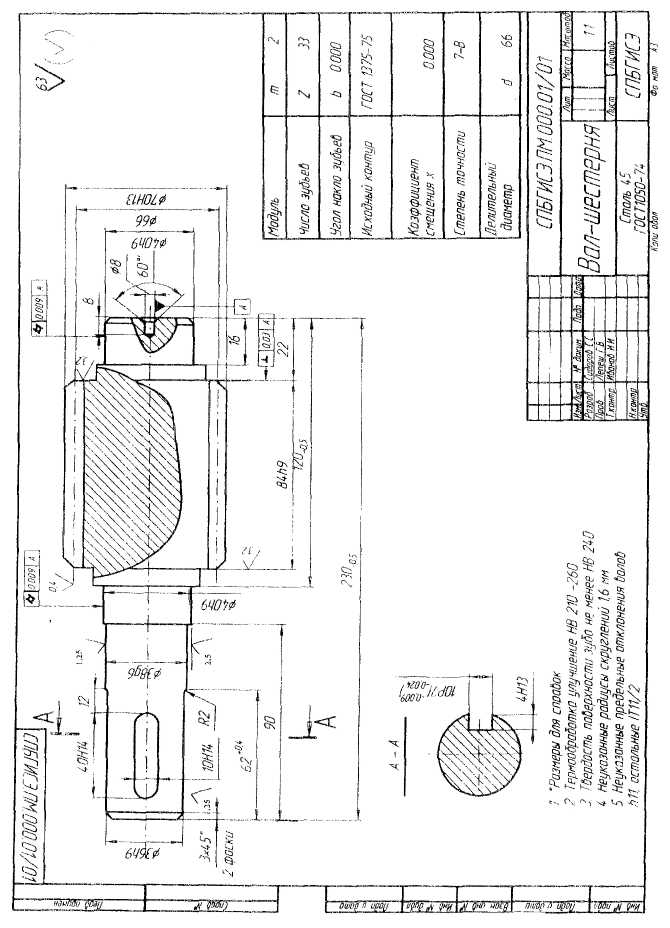
Рис. 12. Чертеж быстроходного вала

Рассмотрим внешние силы, нагружающие быстроходный вал редуктора (рис. 13).

Со стороны муфты от электродвигателя на вал действует крутящий момент T₁ и поперечная сила F_r со стороны зацепления окружная сила F_T и поперечная R₀:

где: F_t – окружное усилие, действующее на зубья муфты

Принимаем F_r = 1041,7 Н.

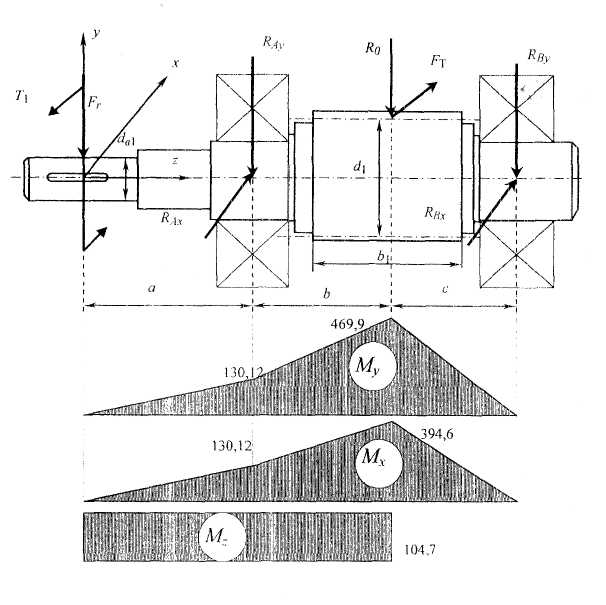
Рис. 13. Расчетная схема вала

Шариковые подшипники
Радиальные	Сферические	Радиально-упорные	Упорные
Роликовые подшипники
Радиальные	Сферические	Радиально-упорные	Упорные

Рис. 14. Виды подшипников качения

Реакции опор R_А и R_В рассчитаем из условий статики. Поскольку направленные силы F_r относительно плоскости действия составляющих реакций неизвестно, то в каждом случае будем добавлять ее абсолютное значение

В соответствии с найденными реакциями строим эпюры изгибающих М_х(z), M_y(z) и крутящих M_z(z) моментов (см. рис. 13):

На участке 0 ≤ z < а => М_x(z) = M_y(z) = – F_r ∙ z = 1041,7 ∙ z;

при z = 0 => M_x(z) = M_y(z) = 0; z = a => M_x(z) = …

… M_y(z) = 1041,7 ∙ 125 ∙ 10^–3 = 130,2 H ∙ м;

На участке 0 ≤ z < а => М_x(z) = – F_r ∙ z = 1041,7 ∙ z;

при z = 0 => M_x(z) = 0;

при z = a => M_x(z) = 1041,7 ∙ 125 ∙ 10^–3 = 130,2 H ∙ м;

На участке a ≤ z < а + b => М_x(z) = – F_r ∙ z = 1041,7 ∙ z – R_Ay ∙ (z – a);

при z = a + b => M_x(z) = 1041,7 ∙ 200 ∙ 10^–3 + 2484 ∙ 75 ∙ 10^–3 = 394,6 H ∙ м;

На участке 0 ≤ z < а => М_y(z) = – F_r ∙ z = 1041,7 ∙ z;

при z = 0 => M_y(z) = 0;

при z = a => M_y(z) = 1041,7 ∙ 125 ∙ 10^–3 = 130,2 H ∙ м

На участке a ≤ z < а + b => M_y(z) = – F_r ∙ z = 1041,7 ∙ z – R_Ax ∙ (z – a);

при z = a + b => M_y(z) = 1041,7 ∙ 200 ∙ 10^–3 + 3488 ∙ 75 ∙ 10^–3 = 469,9 H ∙ м

На участке 0 ≤ z < а + b => М_z(z) = – T₁ = – 104,17 ∙ z;

7.2. Расчет статической прочности вала

Из рис. 13 следует, что опасными сечениями для рассматриваемого вала, которые необходимо проверить на прочность, являются сечения: (z = 0), как наименее жесткое при кручении d_в1 = 26,5 мм, а также сечения (z = a) и (z = a + b), где действуют наибольшие изгибающие моменты.

В сечении (z = 0) находится еще и шпоночный паз, ослабляющий его жесткость. Сечение (z = a), где; действует изгибающий момент

.

и крутящий момент M_z = 104,17 Н ∙ м, находится в сложном напряженном состоянии и при этом имеет диаметр, незначительно превышающий наименьший. В сечении (z = a + b) изгибающий момент достигает наибольшей величины

.

Рассчитаем наибольшие напряжения в опасных сечениях.

В сечении (z = 0) нормальные напряжения от осевых сил и изгибающих моментов равны нулю, касательные напряжения τ_max определяются крутящим моментом М_z = 104,17 H ∙ м и полярным моментом сопротивления сечения W_p цилиндрического конца вала со шпоночным пазом, глубиной t = 5 мм (см. табл. 8).

.

Тогда наибольшие касательные напряжения:

,

а условие прочности вала в сечении (z = 0)

выполняется.

В сечении (z = a) наибольшие нормальные напряжения определяются величиной изгибающего момента М_а = 183,8 Н ∙ м и моментом сопротивления сечения вала

о наибольшие касательные напряжения этого сечения с полярным моментом , равны

.

В качестве допустимых напряжений на изгиб примем

.

При этом условие статической прочности по приведенным напряжениям,

, выполняется.

В сечении (z = a + b) рассчитаем аналогично, с учетом того, что наибольшие нормальные напряжения определяются величиной изгибающего момента и моментом сопротивления сечения вала (с диаметром шестерни по впадинам):

Условие статистической прочности по приведенным напряжениям,

, выполняется.