Расчет собственных значений привода
Собственные значения определяют характеристики свободных колебаний, вынужденных колебаний и устойчивость динамических систем.
Пакет программ PAN для нахождения собственных значений системы реализует следующий алгоритм:
Начало => ввод исходных данных => построение характеристического полинома => определение собственных значений методом Ньютона => вывод действительных частей и собственных частот => конец.
Расчет собственных значений частот
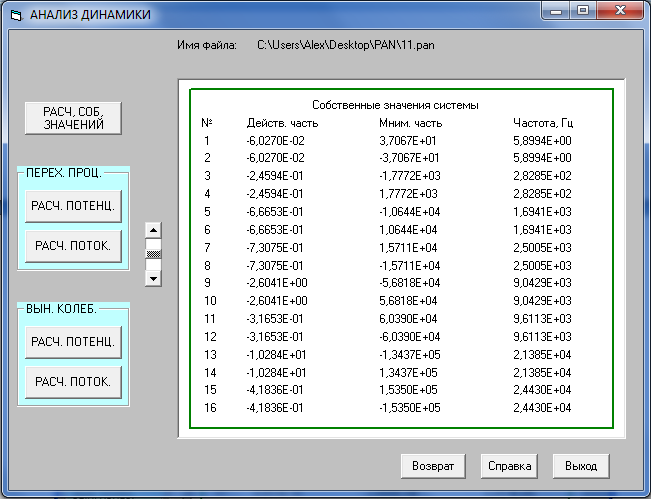
Расчет параметров переходного процесса привода
Исследование переходного процесса является необходимой частью процесса проектирования технических объектов. Оно завершает этап анализа и синтеза системы объекта. На этом этапе исследуют реакцию системы на входные воздействия и получают информацию о протекающих динамических процессах.
Переходный процесс представляет собой изменение во времени параметра при переходе системы (вследствие внешнего воздействия) от одного устойчивого состояния к другому. Используя исходные данные, находим параметры переходного процесса:
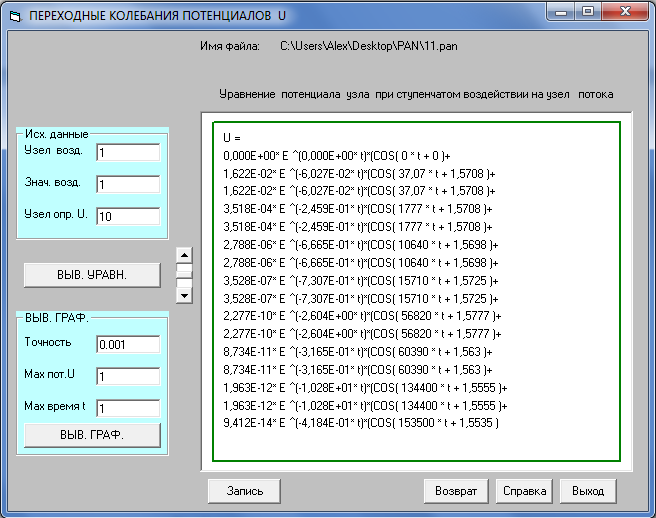
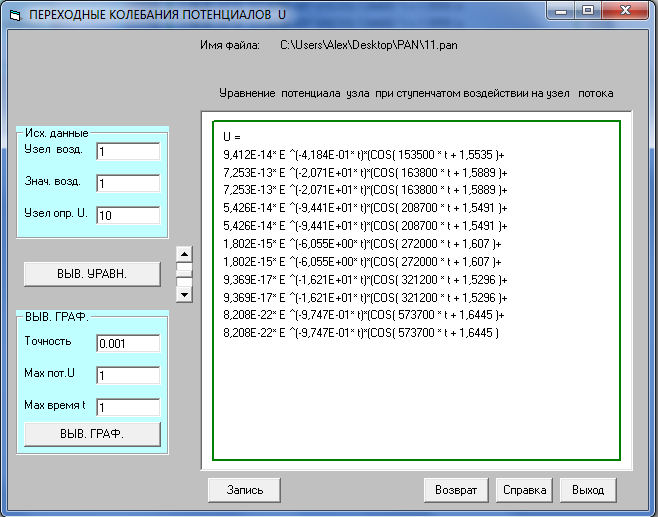
График переходного процесса
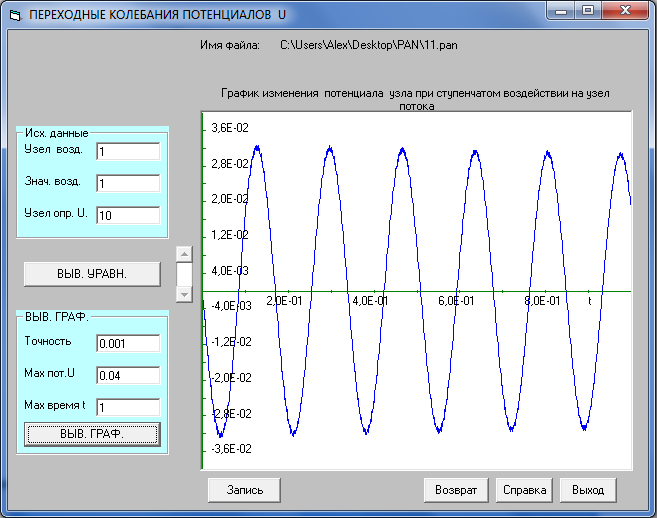
График переходного процесса
Таблица значений вынужденных колебаний при периодическом воздействии на узел 1
Таблица значений вынужденных колебаний при периодическом воздействии на узел 1
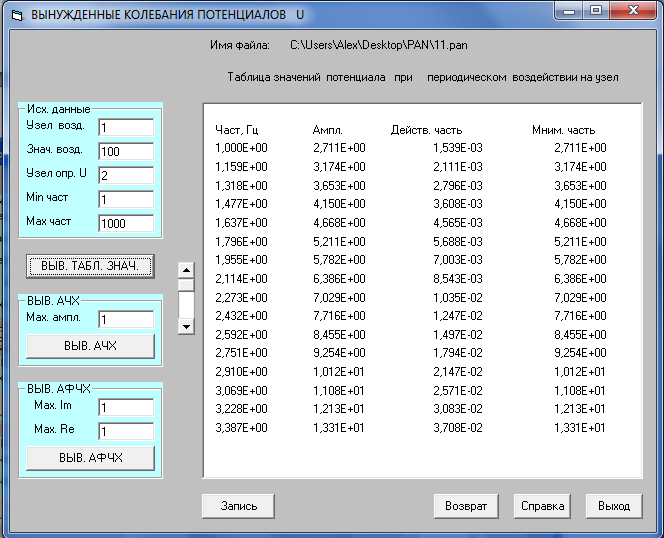
Амплитудно-частотная характеристика шпинделя
Амплитудно-частотная характеристика шпинделя
Пик графика (при частоте 54,4 Гц) соответствуют условиям резонанса системы и определяются параметрами системы. Резонансный режим работы системы (∆ν) определяется перпендикулярами, проведенными от линии, высота которой вычисляется как произведение амплитуды на 0,14.
Рабочий диапазон системы (250-2800 об/мин) находится после резонансного режима работы системы.
Следовательно, в системе, находящейся под действием внешней возмущающей силы, возможны изменения амплитуды. Чтобы снизить влияние вынужденных колебаний, нужно стремиться к уменьшению амплитуды. Это достигается за счет изменения параметров и структуры системы.
Амплитудно-фазочастотная характеристика шпинделя
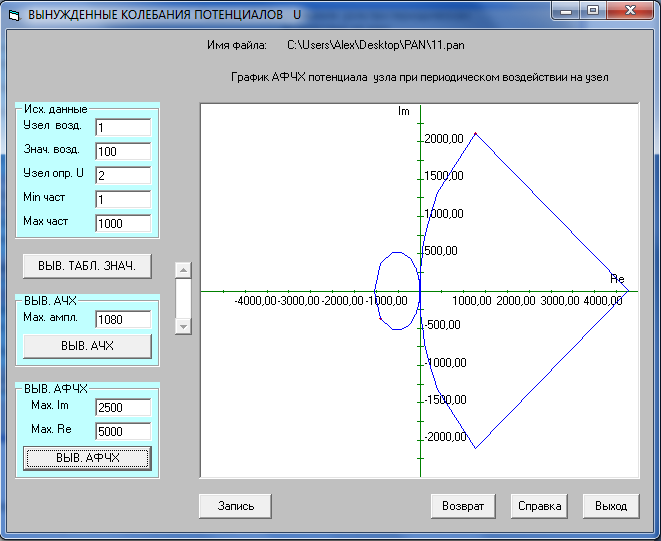
Амплитудно-фазочастотная характеристика шпинделя
Видно, что амплитудно-фазочастотная характеристика не охватывает критическую точку -1, лежащую на вещественной оси, следовательно, система устойчива
Выводы и рекомендации
В данной работе составлена механическая схема и математическая модель системы на основе метода прямой аналогии.
Для исследования свойств и связи элементов в системе были составлены компонентные и топологические уравнения, определены параметры математической модели привода на основе данных, полученных при расчете механической вращательной схемы.
Для определения статических и динамических характеристик системы были проведены исследования на основе требований, предъявляемых к данному приводу. Исследования показали, что шпиндель является наиболее жестким валом. Также был выявлен слабый вал (вал II) и было предложено выполнить его из легированной стали.
Спроектированный привод должен работать при номинальных нагрузках, а это возможно только тогда, когда механическая система привода устойчива. Определить, насколько устойчива та или иная система можно с помощью построения графиков зависимостей одних параметров от других.
По построенным графикам можно сделать вывод, что система устойчива и изменений в конструкцию привода вносить не надо.