
Завдання 9
Статистична сукупність спостережень за пояснюючими змінними моделі прибутку підприємства представлена в наведеній нижче таблиці. Дослідити наявність мультиколінеарності між пояснюючими змінними, скориставшись алгоритмом Фаррара-Глобера.
Таблиця 9.1 – Статистична сукупність спостережень між пояснюючими змінними моделі прибутку підприємства
Місяць |
Прибуток на місяць, грн., Y |
Фондовіддача,грн., X1 |
Продуктивність праці, грн., X2 |
Питомі інвестиції, грн., X3 |
1 |
46 |
16 |
13 |
16 |
2 |
51 |
21 |
10 |
20 |
3 |
61 |
15 |
14 |
18 |
4 |
46 |
28 |
10 |
18 |
5 |
54 |
18 |
14 |
21 |
6 |
45 |
19 |
8 |
22 |
7 |
63 |
18 |
14 |
23 |
8 |
48 |
21 |
18 |
19 |
9 |
59 |
26 |
13 |
21 |
10 |
51 |
32 |
18 |
21 |
11 |
56 |
34 |
20 |
29 |
12 |
54 |
21 |
18 |
22 |
13 |
70 |
22 |
20 |
28 |
14 |
51 |
33 |
11 |
22 |
15 |
52 |
22 |
17 |
29 |
16 |
73 |
24 |
22 |
24 |
17 |
60 |
28 |
24 |
26 |
18 |
54 |
25 |
21 |
22 |
19 |
61 |
29 |
24 |
31 |
20 |
59 |
41 |
21 |
27 |
Розв’язання завдання.
Мультиколінеарність – наявність тісної лінійної залежності, або кореляції, між двома чи більше пояснювальними змінними. Вона негативно впливає на кількісні характеристики економетричної моделі або робить її побудову взагалі неможливою.
Найповніше оцінити
мультиколінеарність можна за допомогою
алгоритму Фаррара-Глобера. Цей алгоритм
має три види статистичних критеріїв,
згідно з якими перевіряється
мультиколінеарність всього масиву
незалежних змінних (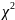 –
«хі»-квадрат); кожної незалежної зміної
з рештою змінних (F-критерій);
кожної пари незалежних змінних
(t-критерій).
–
«хі»-квадрат); кожної незалежної зміної
з рештою змінних (F-критерій);
кожної пари незалежних змінних
(t-критерій).
Усі ці критерії при порівнянні їх із критичними значеннями дають змогу робити конкретні висновки про наявність чи відсутність мультиколінеарності незалежних змінних [5].
Першим кроком стандартизуємо змінні моделі. Елементи стандартизованих векторів обчислимо за формулою:
|
|
де n
– число спостережень (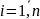 );
);
m – число
пояснювальних змінних (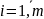 );
);
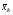 – середнє арифметичне k-ї
пояснювальної змінної;
– середнє арифметичне k-ї
пояснювальної змінної;
 – дисперсія k-ї
пояснювальної змінної.
– дисперсія k-ї
пояснювальної змінної.
У даному випадку n = 20, m = 3. Із приведеної вище формули бачимо, що перш за все необхідно розрахувати середні арифметичні для кожної пояснювальної змінної. Маємо наступні значення:

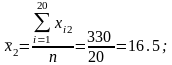
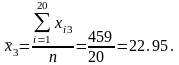
Середньоквадратичні відхилення
для кожної незалежної змінної
мають значення:
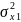 =
6,74;
=
6,74;
 =
4,83;
=
4,83;
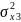 =
4,14.
=
4,14.
Всі розрахункові дані для стандартизації наведені в таблиці 9.2.
Таблиця 9.2 – Розрахункові дані для стандартизації
|
|
|
|
|
|
|
1 |
74,823 |
12,250 |
48,303 |
-1,282 |
-0,723 |
-1,675 |
2 |
13,323 |
42,250 |
8,703 |
-0,541 |
-1,343 |
-0,711 |
3 |
93,123 |
6,250 |
24,503 |
-1,431 |
-0,517 |
-1,193 |
4 |
11,223 |
42,250 |
24,503 |
0,497 |
-1,343 |
-1,193 |
5 |
44,223 |
6,250 |
3,803 |
-0,986 |
-0,517 |
-0,470 |
6 |
31,923 |
72,250 |
0,902 |
-0,838 |
-1,756 |
-0,229 |
7 |
44,223 |
6,250 |
0,003 |
-0,986 |
-0,517 |
0,012 |
8 |
13,323 |
2,250 |
15,603 |
-0,541 |
0,310 |
-0,952 |
9 |
1,823 |
12,250 |
3,803 |
0,200 |
-0,723 |
-0,470 |
10 |
54,023 |
2,250 |
3,803 |
1,090 |
0,310 |
-0,470 |
11 |
87,423 |
12,250 |
36,603 |
1,386 |
0,723 |
1,458 |
12 |
13,323 |
2,250 |
0,902 |
-0,541 |
0,310 |
-0,229 |
13 |
7,022 |
12,250 |
25,503 |
-0,393 |
0,723 |
1,217 |
14 |
69,723 |
30,250 |
0,902 |
1,238 |
-1,136 |
-0,229 |
15 |
7,022 |
0,250 |
36,603 |
-0,393 |
0,103 |
1,458 |
Продовження таблиці 9.2
|
|
|
|
|
|
|
16 |
0,422 |
30,250 |
1,103 |
-0,096 |
1,136 |
0,253 |
17 |
11,223 |
56,250 |
9,303 |
0,497 |
1,550 |
0,735 |
18 |
0,123 |
20,250 |
0,902 |
0,052 |
0,930 |
-0,229 |
19 |
18,923 |
56,250 |
64,803 |
0,645 |
1,550 |
1,941 |
20 |
267,323 |
20,250 |
16,403 |
2,424 |
0,930 |
0,976 |
Σ |
864,550 |
445,000 |
326,950 |
|
|
|
Отже, значення змінних , , утворюють матрицю нормалізованих значень Х.
Наступним кроком знаходимо кореляційну матрицю, що розраховується за формулою:
|
(9.2) |
де 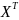 – матриця транспонована до матриці Х.
– матриця транспонована до матриці Х.
Для даного завдання кореляційна матриця матиме наступний вигляд:
.
|
(9.3) |
Обчислимо критерій Пірсона для даної задачі за наступною формулою:
|
(9.4) |
де 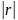 – визначник кореляційної
матриці.
– визначник кореляційної
матриці.
Значення цього критерію
порівняємо із табличним при ступені
свободи та рівні значущості α = 0,05.
Значення критерію Пірсона за розрахованою
формулою χ2
=13,93, а табличне значення критерію –
χ2табл
= 7,815. Бачимо, що χ2 >
χ2табл,
отже в масиві змінних існує
мультиколінеарность.
та рівні значущості α = 0,05.
Значення критерію Пірсона за розрахованою
формулою χ2
=13,93, а табличне значення критерію –
χ2табл
= 7,815. Бачимо, що χ2 >
χ2табл,
отже в масиві змінних існує
мультиколінеарность.
Наступним кроком обчислимо F-критерії. Для їх визначення спочатку треба знайти матрицю С, яка є оберненою до матриці r. Матриця С має вигляд:
|
|
Використовуючи діагональні елементи матриці С, розрахуємо F-критерії, використовуючи формулу:
|
|
де Ckk – діагональний елемент матриці С.
Отже, F-критерії матимуть наступні значення: F1=2,581; F2=6,385; F3=7,809. Обчислені критерії порівнюються з табличним значенням F=8,69 при рівні значущості α=0,05 та коли є 17 ступенів свободи.
Як бачимо, всі розраховані F менше F табличного, що дає змогу стверджувати, що ці змінні не є мультиколінеарними між собою.
Далі визначимо частинні коефіцієнти кореляції r. Частинні коефіцієнти кореляції показують тісноту зв’язку між двома пояснюючими змінними за умови, що всі інші змінні не впливають на цей зв’язок і обчислюються за формулою:
|
|
Отже, маємо наступні значення
частинних коефіцієнтів кореляції:
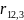 =0,117;
=0,117;
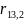 =-0,31;
=-0,31;
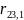 =0,57.
=0,57.
Отже, спираючись на отримані значення окремих (частинних) коефіцієнтів кореляції, можна сказати, що зв’язу між фондовіддачею та продуктивністю праці не існує, якщо не враховувати вплив питомих інвестицій, зв’язку між фондовіддачею та питомими інвестиціями також фактично не існує, якщо не брати до уваги вплив продуктивності праці. Зв’язок між продуктивністю праці та питомими інвестиціями є слабким, якщо не враховувати фондовіддачу.
Визначимо t-критерій. Ці критерії застосовуються для визначення мультиколінеарності двох пояснюючих змінних і обчислюються за формулою:
|
|
Маємо наступні значення t-критеріїв: t12=0,486; t13=-1,373; t23=2,892.
Обчислені t-критерії порівнюються з табличним значенням (t=1,74), коли маємо 17 ступенів свободи та при рівні значущості α=0,05.
Оскільки t23 > tтабл, то продуктивність праці питомі інвестиції є відповідно мультиколінеарними між собою; а інші змінні не є мультиколінеарними між собою.
Отже, за допомогою алгоритму Фаррара-Глобера було доведено, що між пояснюючими змінними у даній моделі існує мультиколінеарність. Тому для того, щоб застосовувати метод найменших квадратів, спочатку треба позбавитися мультиколінеарності.

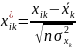 ,
(9.1)
,
(9.1)
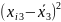
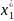
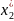
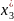
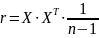 ,
,
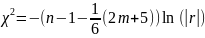 ,
, (9.5)
(9.5)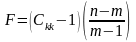 (9.6)
(9.6)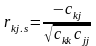 .(9.7)
.(9.7)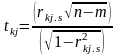 (9.8)
(9.8)