
Завдання 6
Розв’язати задачу опуклого програмування.
Z=x21+x22-6x1-4x2 (min);
x1 + 2x2 ≤ 12;
2x1 + x2 ≤ 6;
x1 ≥ 0, x2 ≥ 0, x3≥ 0
Розв’язання завдання.
Розв’яжемо дану задачу за допомогою методу множників Лагранжа, а потім застосуємо теорему Куна-Таккера. Метод множників Лагранжа був описаний у попередньому завданні, тому перейдемо безпосередньо до розрахунків.
Запишемо функцію Лагранжа для поставленої задачі. Вона матиме наступний вигляд:
Наступним кроком знаходимо частинні похідні за всіма змінними функції L, а потім прирівнюємо їх до нуля. Отримаємо наступну систему:
|
|
Розв’язавши дану систему
отримаємо стаціонарні точки
та
– стаціонарні точки. Для
даної системи
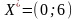 та
та
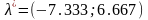 .
.
Значення функції в цій точці наведені на рисунку 6.1
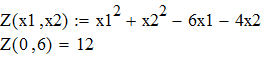
Рисунок 6.1 – Значення функції в точці екстремуму
Застосуємо теорему Куна-Таккера.
Якщо задано є задача нелінійного
програмування, де функції
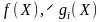
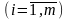 диференційовні і вгнуті по Х,
то для того, щоб вектор
диференційовні і вгнуті по Х,
то для того, щоб вектор
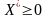 був розв’язком цієї задачі, необхідно
і достатньо, щоб існував такий вектор
був розв’язком цієї задачі, необхідно
і достатньо, щоб існував такий вектор
 ,
що пара (
,
що пара ( ,
, )
була б сідловою точкою функції Лагранжа,
тобто щоб виконувалися умови,зображені
на рис 6.2:
)
була б сідловою точкою функції Лагранжа,
тобто щоб виконувалися умови,зображені
на рис 6.2:
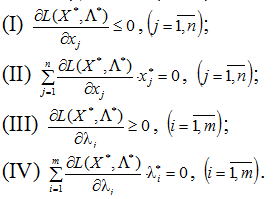
Рисунок 6.2 – Умови що вказують на те, що знайдена точка – сідлова
Тепер підставимо значення Х* у наведені вище умови. Отримаємо:
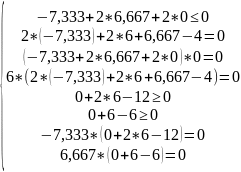
З наведеного вище рівняння бачимо, що точка Х* задовольняє всім умовам теореми Куна – Таккера, а отже є сідловою точкою функції Лагранжа і рішенням задачі опуклого програмування.
Рисунок 6.3 – Вирішення завдання у MathCad
Завдання 7
Створити інформаційну базу
у вигляді матриці котирувань продажу
(С) n видів акцій
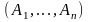 у періоди часу t, t
=0,...,T (вказати джерело
інформації):
у періоди часу t, t
=0,...,T (вказати джерело
інформації):
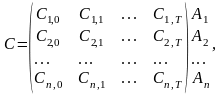
де Сi,t (i =1, ... ,n; t = 0, ... ,T) – ціна і-тої акції у періоді часу t, n>=5, T>=10.
Здійснити порівняльний аналіз ризикованості інвестування у цінні папери на основі даних про котирування цінних паперів з матриці С.
Аналіз здійснити на основі показників:
середньоквадратичного відхилення (σ) норми прибутку цінного паперу;
семіквадратичного відхилення (SSV) норми прибутку цінного паперу;
коефіцієнта варіації (CV) для кожного виду цінного паперу;
коефіцієнта семіваріації (SV) для кожного виду цінного паперу.
Проаналізувати привабливість цінних паперів на основі розрахованих показників.
Розв’язання завдання.
Оцінювання ризику – необхідний атрибут у стратегії і тактиці ефективного менеджменту. Тому важливою є розробка методик кількісної оцінки ступеня ризику, удосконалення механізму моніторингу, контролювання економічного ризику та керування ним на засадах системного аналізу.
Зробимо порівняльний аналіз ризикованості інвестування в цінні папери на основі даних про котирування акцій українських підприємств впродовж 2010 - 2011 років. Дані взяті з електронного ресурсу, розміщеного за адресою: www.i-nvest.net (таблиця 7.1).
Таблиця 7.1 – Котирування акцій українських підприємств впродовж 2010-2011 рр.
Емітент |
Періоди |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
ОАО «Киевградосервис» |
12,8 |
13,2 |
13,3 |
13,1 |
13,7 |
13,8 |
14,0 |
14,1 |
14,1 |
14,6 |
12,8 |
ОАО «Берест» |
21,6 |
21,9 |
21,9 |
21,8 |
21,8 |
21,5 |
21,3 |
22,0 |
22,0 |
21,7 |
21,6 |
ОАО «Гранд-Інвест IК» |
28,6 |
28,8 |
28,9 |
30,1 |
30,2 |
30,2 |
30,1 |
28,8 |
28,5 |
28,6 |
28,6 |
ОАО «Градострой» |
7,8 |
7,4 |
7,6 |
7,3 |
7,3 |
7,0 |
6,9 |
6,8 |
6,5 |
6,4 |
7,8 |
ОАО «Гранит» |
42,4 |
42,6 |
42,6 |
42,8 |
43,7 |
44,0 |
43,5 |
44,0 |
44,0 |
44,2 |
42,4 |
ОАО «ДБК-1» |
12,4 |
12,3 |
12,8 |
13,0 |
13,1 |
13,1 |
13,3 |
13,7 |
13,9 |
13,6 |
12,4 |
Основною характеристикою акції є норма прибутку. Норма прибутку цінних паперів залежить від трьох факторів: ціни покупки, проміжних виплат (дивідендів) та ціни продажу [1].
Тоді, норма прибутку звичайної акції у період часу t визначається за формулою:
|
|
де Ri,t – норма прибутку і-ї акції;
Ci,t – ціна і-ї акції у період часу t;
di,t – дивіденди, що виплачуються у період часу t по і-й акції.
На основі наведеної вище формули створимо таблицю норми прибутку (табл. 7.2).
Таблиця 7.2 – Норма прибутку по кожному виду акцій
R1 |
0,02 |
0,03 |
0,00 |
-0,01 |
0,04 |
0,01 |
0,02 |
0,01 |
0,00 |
0,03 |
R2 |
0,01 |
0,01 |
0,00 |
0,00 |
0,00 |
-0,01 |
-0,01 |
0,03 |
0,00 |
-0,01 |
R3 |
0,00 |
0,00 |
0,00 |
0,04 |
0,00 |
0,00 |
0,00 |
-0,04 |
-0,01 |
0,01 |
R4 |
0,02 |
-0,06 |
0,03 |
-0,03 |
-0,01 |
-0,04 |
-0,02 |
0,00 |
-0,05 |
-0,02 |
R5 |
0,00 |
0,01 |
0,00 |
0,00 |
0,02 |
0,01 |
-0,01 |
0,01 |
0,00 |
0,01 |
R6 |
0,00 |
-0,01 |
0,04 |
0,02 |
0,01 |
0,00 |
0,01 |
0,03 |
0,01 |
-0,02 |
Приймаємо гіпотезу, що норми прибутку акцій є випадковими величинами. Тоді на основі таблиці 7.2 ми можемо обчислити статистичну оцінку сподіваної норми прибутку для кожного виду акцій. Його можна розглядати як результат, котрий ми очікуємо отримати в середньому. Оцінку сподіваної норми прибутку будемо розраховувати за формулою:
|
|
Після проведення розрахунків отримаємо: m1 = 0,0154; m2 = 0,0012; m3 = 0,0002; m4 = -0.0173; m5 = 0,0046; m6.=0,0101
Для оцінювання степеню ризику використаємо варіацію (дисперсію) можливих результатів навколо сподіваного прибутку та середньоквадратичне відхилення.
Статистична оцінка дисперсії норми прибутку обчислюється за формулою:
|
(7.3) |
Формула для обчислення статистичної оцінки середньоквадратичного відхилення норми прибутку має вигляд:
|
(7.4) |
Маємо наступні оцінки міри розсіювання можливих результатів навколо сподіваного прибутку: D(R1) = 0,00025; D(R2) = 0,00017; D(R3) = 0,00044; D(R4) = 0,00073; D(R5) = 0,0006; D(R6) = 0.00031.
Значення середньоквадратичного відхилення мають наступний вигляд: 1 = 0.016; 2 = 0,013; 3 = 0,021; 4 = 0,027; 5 = 0,008; 6 =0,018.
Отже, вкладання грошей в акції ОАО «Гранит» є менш ризикованим, що підтверджують як значення дисперсії, так і значення середньоквадратичного відхилення.
Якщо випадкова величина Х відображає прибутки, і має місце від’ємне відхилення, то це є ознакою несприятливої ситуації. В той же час додатне відхилення вказує на те, що реалізація випадкової величини (прибутку) є більшою, ніж сподівана величина, і це для інвестора є, очевидно, кращою тобто сприятливою ситуацією.
Реалізацією саме цього підходу є такі оцінки як семіваріація і семіквадратичне відхилення.
Для розрахунку значення семіваріації скористаємось формулою:
|
(7.5) |
де αi,t – індикатор несприятливих відхилень, який розарховується за наступною формулою:
|
(7.6) |
Маємо наступні значення семіваріації: SV(R1) = 0,0001; SV(R2) = 0,0001; SV(R3) = 0,0002; SV(R4) = 0,0003; SV(R5) = 0,00003; SV(R6) = 0,0001.
З практичного погляду зручніше застосовувати так зване семіквадратичне відхилення, яке можна подати за формулою:
|
(7.7) |
Провівши розрахунки за приведеною вище формулою, отримаємо SSV(R1) = 0,011; SSV(R2) = 0,007; SSV(R3) = 0,015; SSV(R4) = 0,018; SSV(R5) = 0,005; SSV(R6) = 0,012.
Отже, можна сказати, що чим більшою буде величина SV(Rі) чи SSV(Rі), тим більшим буде ступінь ризику.
Коли сподівані доходи проектів суттєво різняться між собою, то для порівняння їх ризикованості неадекватно використовувати оцінки ступеня ризику, задані в абсолютному вираженні. У цьому разі можна скористатися такими показниками ризикованості, як коефіцієнт варіації (CV) та коефіцієнт семіваріації (CSV), які обчислюються відповідно за формулами (7.8) та (7.9):
|
|
|
|
Значення коефіцієнта варіації для даних завдання матиме наступний вигляд: CV1 = 1,033; CV2 = 10,715; CV3 = 134,56; CV4 = -1,055; CV5 =1,141; CV6 = 1,182.
Коефіцієнт семіваріації набуває значень: CSV1 = 0,709; CSV2 = 5,891; CSV3 = 99,087; CSV4 = -1,055; CSV5 = 1,141; CSV6 = 1,182
Цим коефіцієнтам можна надати таке економічне трактування: коефіцієнт варіації це величина ризику відхилень, що припадають на одиницю сподіваного доходу, а коефіцієнт семіваріації величину ризику несприятливих відхилень, що припадають на одиницю сподіваного доходу. А тому можна дійти висновку, що ці коефіцієнти мають від’ємний інгредієнт (чим менші їх значення для проекту, тим меншим ризиком у відносному вираженні він обтяжений).
Слід зауважити, що дані коефіцієнти можуть використовуватися лише за умови, що економічний показник Х, з позиції якого аналізуються проекти, має додатний інгредієнт і при цьому його сподіване значення більше нуля.
Отже, на основі розрахованих показників можна стверджувати, що найбільш привабливими є акції ОАО «Гранит» та ОАО «Градострой».

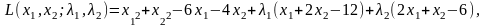 (6.1)
(6.1)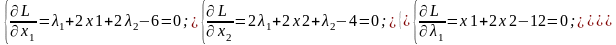
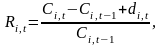 (7.1)
(7.1)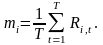 (7.2)
(7.2)
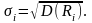
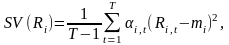
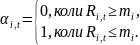
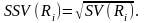
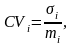 (7.8)
(7.8)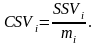 (7.9)
(7.9)