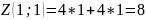Завдання 5
Визначити точку та характер умовного екстремуму функції за методом множників Лагранжа.
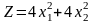 ,
,
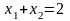
Розв’язання завдання.
Одним із методів розв’язання задач нелінійного програмування є метод множників Лагранжа [4].
Цей метод використовється для розв’язання задач виду:
|
(5.1) |
за умов:
|
(5.2) |
де функції
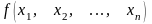 і
і
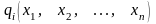 диференційовані.
диференційовані.
Ідея цього методу полягає у заміні поставленої задачі на простішу: на знаходження екстремуму складнішої функції, але без обмежень. Ця функція має назву функції Лагранжа. Вона має наступний вигляд:
|
|
де 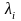 – деякі невідомі величини, що називаються
множниками Лагранжа.
– деякі невідомі величини, що називаються
множниками Лагранжа.
Запишемо функцію Лагранжа для поставленої задачі. Вона матиме наступний вигляд:
|
(5.4) |
Наступним кроком знаходимо частинні похідні за всіма змінними функції L, а потім прирівнюємо їх до нуля. Отримаємо наступну систему:
|
|
Розв’язавши дану систему
отримаємо стаціонарні точки
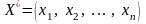 та
та
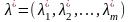 – стаціонарні точки. Для
даної системи
– стаціонарні точки. Для
даної системи
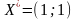 та
та
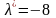 .
.
Щоб визначити характер
умовного екстремуму, за функцією Лагранжа
будуємо матрицю Гессе розмірністю
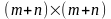 .
Ця матриця має блочний характер:
.
Ця матриця має блочний характер:
|
|
де О – матриця розмірністю (m×m), що складається з нульових елементів,
Р – матриця розмірністю (m×n), елементи якої визначаються наступним чином:
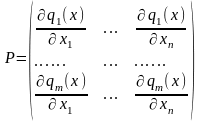 (5.7)
(5.7)
Р′ – транспонована матриця до Р розмірністю (n×m),
Q – матриця розмірністю (n× n) виду:
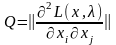 ,
,
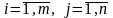 (5.8)
(5.8)
Для поставленої задачі матриця Гессе матиме вигляд:
|
(5.9) |
Розрахувавши мінори даної матриці (Δ4 = 64, Δ5 = 8), отримаємо незнакозмінний числовий ряд, що означає, що Х* – точка мінимуму.
Далі обчислимо значення цільової функції у цій точці.
|
(5.10) |
Отже, використавши метод
множників Лагранжа, з’ясовано, що Х*=(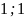 )
– точка мінимуму.
)
– точка мінимуму.
Для того, щоб перевірити правильність виконання даного завдання, скористаємося програмним забезпеченням MathCad (рис. 5.1).
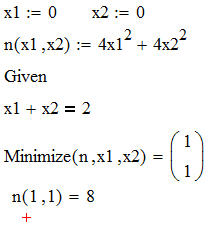
Рисунок 5.1 – Вирішення завдання у MathCad

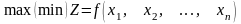
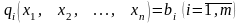
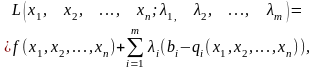 (5.3)
(5.3)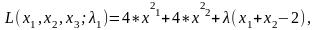
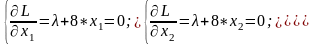 (5.5)
(5.5)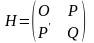 (5.6)
(5.6)