Завдання 4

Однорідний вантаж, зосереджений у m постачальників в обсягах 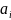( 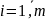), необхідно поставити n споживачам в обсягах ( ).

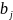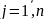Відомі 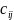( ; ) – вартості перевезення одиниці вантажу від кожного i-го постачальника до кожного j-го споживача.

Необхідно скласти такий план перевезень, використовуючи метод stepping-stone, при якому запаси усіх постачальників вивозяться повністю й сумарні витрати на перевезення усього вантажу мінімальні. Вхідні дані транспортної задачі наведені у таблиці 4.1.

Таблиця 4.1 – Вхідні дані задачі

Постачальник	Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача				Запаси
	Замовник
	В1	В2	В3	В4
А1	1	2	6	4	40
А2	3	1	3	2	30
А3	5	7	5	1	20
Потреба	30	25	18	20

Розв’язання завдання.

Транспортна задача – це специфічна задача лінійного програмування, що застосовується для визначення найекономічнішого плану перевезення однорідної продукції від постачальників до споживачів.

Перш за все побудуємо математичну модель задачі. Нехай x_ij – кількість продукції, що перевозиться від і-го постачальника до j-го замовника 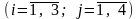. Загальні витрати на транспортування визначаються як сума добутків обсягів перевезеної продукції на вартість транспортування одиниці продукції до відповідного замовника. Витрати мають бути мінімальними.

За умовою, дана транспортна задача є незбалансованою. Щоб збалансувати дану задачу, необхідно ввести фіктивного споживача, перевезення до якого дорівнюють 0. Збалансована транспортна задача наведена в таблиці 4.2.

Таблиця 4.2 – Збалансована транспортна задача

Постачальник	Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача				Запаси
	Замовник
	В1	В2	В3	В4
А1	1	2	6	4	40
А2	3	1	3	2	30
А3	5	7	5	1	20
A4	0	02	0	0	3
Потреба	30	25	18	20

Для розв’язання даної задачі скористаємося методом потенціалів. Для початку побудуємо базове рішення задачі, використовуючи метод северно-західного кута.

Рішення задачі представлене в таблиці 4.3.

Таблиця 4.3 – Перший опорний план, побудований за методом северно-західного кута

Постачальник	Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача					Запаси
	Замовник
	В1	В2	В3	В4
А1	1[30]	2[10]	6	4	40
А2	3	1[15]	3[15]	2	30
А3	5	7	5[3]	1[17]	20
A4	0	0	0	0[3]	3
Потреба	30	25	18	20

Реалізація першого опорного плану призведе до наступних загальних витрат:

Z = 1*30+2*10+1*15+3*15+5*3+1*17+0*3=142

(4.1)

Одержано опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.

Число зайнятих клітин таблиці, їх 7, m + n - 1 = 7. Отже, опорний план є невиродженим.

Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали ui, vi. по зайнятих клітинам таблиці, в яких ui + vi = cij, вважаючи, що u1 = 0.

Таблиця 4.4 – Попередні потенціали ui, vi

	v1=1	v2=2	v3=4	v4=0
u1=0	1[30]	2[10]	6	4
u2=-1	3	1[15]	3[15]	2
u3=1	5	7	5[3]	1[17]
u4=0	0	0	0	0[3]

Опорний план не є оптимальним, тому що існують оцінки вільних клітин,для яких ui +vi> cijВибираємо максимальну оцінку вільної клітини (4,3): 0Для цього в перспективну клітку (4, 3) поставимо знак «+», а в інших вершинахбагатокутника чергуються знаки «-», «+», «-».

Таблиця 4.5 – Оцінка плану

Постачальник	Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача				Запаси
	Замовник
	В1	В2	В3	В4
А1	1[30]	2[10]	6	4	40
А2	3	1[15]	3[15]	2	30
А3	5	7	5[3][-]	1[17][+]	20
A4	0	0	0[+]	0[3][-]	3
Потреба	30	25	18	20

З вантажів хij стоять в мінусових клітинах, вибираємо найменше, тобто у = min (4, 4) = 3. Додаємо 3 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 3 з Хij, що стоять в мінусових клітинах. В результаті отримаємо новий опорний план.

Таблиця 4.6 – Другий опорний план

Постачальник	Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача					Запаси
	Замовник
	В1	В2	В3	В4
А1	1[30]	2[10]	6	4	40
А2	3	1[15]	3[15]	2	30
А3	5	7	5[0]	1[20]	20
A4	0	0	0[3]	0	3
Потреба	30	25	18	20

Таблиця 4.7 – Попередні потенціали ui, vi

	v1=1	v2=2	v3=4	v4=0
u1=0	1[30]	2[10]	6	4
u2=-1	3	1[15]	3[15]	2
u3=1	5	7	5[0]	1[20]
u4=-4	0	0	0[3]	0

Опорний план є оптимальним, оскільки всі оцінки вільних клітин задовольняють умові u_i + v_i <= c_ij.

Реалізація першого опорного плану призведе до наступних загальних витрат:

Z = 1*30+2*10+1*15+3*15+5*0+1*20+0*3=130

(4.3)

Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается, как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки. Транспортная задача является по теории сложности вычислений NP-сложной и входит в класс сложности NP. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).

Перевіримо правильність виконання завдання за допомогою MathCad (рис. 4.3).

Рисунок 4.3 – Результат вирішення транспортної задачі