
Севастопольський інститут банківської справи Української академії банківської справи Національного банку України Кафедра економічної кібернетики ПОЯСНЮВАЛЬНА ЗАПИСКА до курсової роботи з дисципліни «Економіко-математичне моделювання: оптимізаційні методи та моделі» на тему: «Розв’язання оптимізаційних економічних задач» Варіант 5 Виконав студент II курсу групи ЕК-01 ________________ С.Є. Девятілов Керівник канд. екон. наук, доц. ________________ С.О. Хайлук Побудова та зміст документа відповідає вимогам ДСТУ 3008-95 ______________В.В. Колдовський Севастополь – 2012 ЗМІСТ
ВСТУП 3
ЗАВДАННЯ 1 4
ЗАВДАННЯ 2 8
ЗАВДАННЯ 3 12
ЗАВДАННЯ 4 18
ЗАВДАННЯ 5 24
ЗАВДАННЯ 6 28
ЗАВДАННЯ 7 31
ЗАВДАННЯ 8 37
ЗАВДАННЯ 9 45
ЗАВДАННЯ 10 52
ВИСНОВКИ 56
ПЕРЕЛІК ПОСИЛАНЬ 57
ВСТУП
В умовах ринкової економіки, коли кожній господарській одиниці треба самостійно ухвалювати рішення, стає необхідним математичний розрахунок. Тому роль математичних методів в економіці постійно зростає.
Економіко-математичне моделювання є галуззю економічної науки, яка вивчає основні принципи та інструментарій постановки економічних задач, побудови їх математичних моделей, методів розв’язування та аналізу економічних задач. Застосування економіко-математичних методів і моделей в економіці дозволяє істотно поліпшити якість планування і отримати додатковий ефект без залучення до виробництва додаткових ресурсів.
Метою курсової роботи є вивчення методів розв’язування різних типів економічних задач. У роботі розглядаються основні методи розв’язування, аналізу та використання задач на знаходження екстремуму функції на множині допустимих варіантів у широкому спектрі теоретико-економічних та практичних проблем.
Завдання 1
Побудувати на площині множину (багатокутник) розв’язків системи лінійних обмежень-нерівностей і графічним методом знайти найбільше та найменше значення цільової функції в цьому багатокутнику (x10, x20).
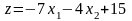
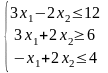
Розв’язання завдання.
Дана задача лінійного програмування містить в собі лише дві змінні, тому вона може бути розв’язана за допомогою графічного методу, що базується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування [3].
Першим кроком необхідно побудувати на площині прямі лінії, рівняння яких можна знайти, замінивши знаки нерівностей в обмеженнях задачі на знаки рівностей. У результаті отримаємо наступні графіки прямих (рис. 1.1).
Наступним кроком визначаємо півплощини, що відповідають кожному обмеженню задачі. Оскільки у даному випадку x10 та x20, то обмежимося першим квадрантом системи координат. Для того, щоб визначити необхідну півплощину, необхідно взяти будь-яку точку на площині та перевірити, чи задовольняють її координати задане обмеження. Якщо точка задовольняє обмеження, то дана півплощина і є геометричним відображенням нерівності. Якщо ж ні, то геометричним зображенням нерівності є інша півплощина. Півплощини розв’язків зображені штриховкою на рисунку 1.1.
Дана фігура є обмеженою з усіх боків і тому вона набуває як мінімального значення так і максимального
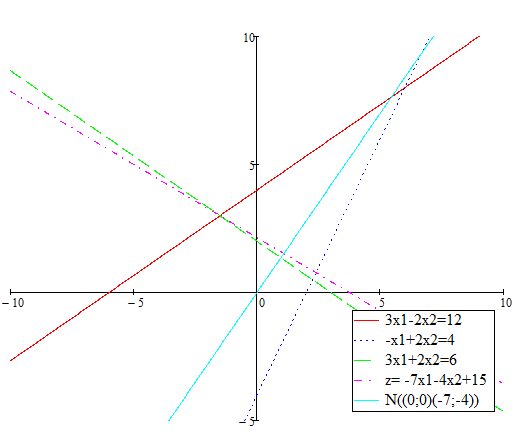
Рисунок 1.1 – Графічне зображення розв’язку задачі лінійного програмування
Далі будуємо вектор, що задає
напрям зростання значень цільової
функції задачі. У даному випадку це
вектор
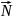 = (-7; -4).
Координати цього вектора – це коефіцієнти
при змінних цільової функції. Цей вектор
виходить із початку координат і проходить
через точку (-7; -4).
= (-7; -4).
Координати цього вектора – це коефіцієнти
при змінних цільової функції. Цей вектор
виходить із початку координат і проходить
через точку (-7; -4).
Наступним кроком будуємо пряму с1х1 + с2х2 = const, перпендикулярну вектору . Для даної задачі побудуємо пряму -7х1-4х2+15=0. Пересуваючи пряму паралельно самій собі у напрямі вектора , знайдемо найвищу (А) й найнижчу (В) точку багатокутника.
Координати точки А є розв’язком системи рівнянь:
|
(1.1) |
|
(1.2)
|
Із даної системи рівнянь х1 = 8, х2 =6. Отже, min Z = -65.
Координати точки В також є розв’язком системи рівнянь:
|
(1.3) |
|
(1.4)
|
Із даної системи рівнянь х1 = 0.5, х2 =2.25. Отже, max Z = 2.5.
Для того, щоб перевірити правильність вирішення поставленої задачі, скористаємося пакетом MathCad. Для знаходження максимуму та мінімуму функції використаємо функції Maximize та Minimize.
Результати розрахунків представлені на рис. 1.2, 1.3.
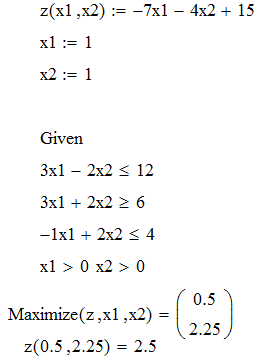
Рисунок 1.2 – Розрахунок максимуму функції
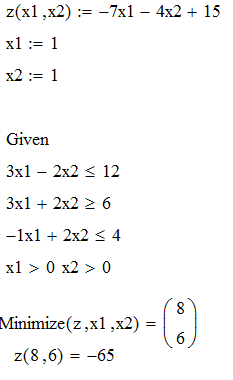
Рисунок 1.3 – Розрахунок мінімуму функції
Завдання 2
Симплексним методом знайти розв’язок задачі лінійного програмування.

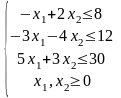
Розв’язання завдання.
Для розв’язання задач лінійного програмування, окрім графічного методу, також використовують симплекс-метод, який є більш універсальним, так як за його допомогою можна шукати оптимальні плани задач лінійного програмування, що у своєму складі мають більше, ніж дві змінні. Процес розв’язання задачі симплекс-методом має ітераційний характер: обчислювальні процедури одного й того самого типу повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або буде з’ясовано, що його не існує [3].
Щоб розв’язати поставлену задачу лінійного програмування, перш за все необхідно записати дану задачу в канонічному вигляді. Для цього перейдемо від обмежень-нерівностей до рівнянь, увівши додаткові змінні в обмеження. Система рівнянь матиме вигляд:
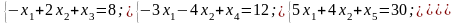 (2.1)
(2.1)
|
|
У цільовій функції задачі додаткові змінні мають коефіцієнти нуль.
|
(2.2) |
Далі необхідно записати задачу у векторній формі. Опорний план задачі утворюють m одиничних лінійно незалежних векторів, що становлять базис m-вимірного простору (m – кількість обмежень у задачі лінійного програмування).
|
(2.3) |
де
|
|
Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні – вільними. Їх прирівнюємо до нуля та з кожного обмеження задачі визначаємо значення базисних змінних. У такий спосіб отримуємо початковий опорний план задачі лінійного програмування. У даному випадку, прирівнявши вільні змінні до нуля, з кожного обмеження дістанемо наступні значення базисних змінних:
|
(2.5) |
Згідно з визначеними
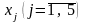 векторна форма запису системи обмежень
цієї задачі матиме вигляд:
векторна форма запису системи обмежень
цієї задачі матиме вигляд:
|
(2.6) |
Другим кроком будуємо симплексну таблицю для перевірки оптимальності опорного плану.
Отже, перший опорний план задачі матиме вигляд, представлений у таблиці 2.1.
Таблиця 2.1 – Перша симплексна таблиця
Базисні змінни |
Вільні члени |
X1 |
X2 |
X3 |
8 |
-1 |
2 |
X4 |
12 |
-3 |
-4 |
X5 |
30 |
5 |
3 |
F |
0 |
-6 |
12 |
Так як у стовпці вільних членів немає від’ємних елементів, то знайдено допустиме рішення. Так як у рядку F є від’ємні елементи, то отримане рішення не оптимально. Для визначення ведучого стовпчика знайдемо максимальний по модулю від’ємний елемент у рядку F (-6). А ведучий рядок тій, у якого найменше позитивне відношення вільного члена до відповідного елементу ведучого стовпця.
Усі елементи наступної симплексної таблиці розраховують за правилом прямокутника. Щоб визначити будь-який елемент нової таблиці за цим правилом, необхідно в попередній симплексній таблиці скласти умовний прямокутник, вершини якого утворюються такими числами:
1 – розв’язувальний елемент;
2 – число, що стоїть на місці елемента нової симплексної таблиці, який ми маємо розрахувати;
3 та 4 – елементи, що розміщуються в двох інших протилежних вершинах умовного прямокутника.
Необхідний елемент нової симплексної таблиці визначаємо за формулою 2.7.
|
|
Таблиця 2.2 – Друга симплексна таблиця
Базисні змінни |
Вільні члени |
X1 |
X4 |
X3 |
14 |
0,2 |
2,6 |
X2 |
30 |
0,6 |
-2,2 |
X5 |
6 |
0,2 |
0,6 |
F |
36 |
1,2 |
15,6 |
Так як у рядку F немає від’ємних елементів, то отримане рішення оптимально.
Отже, оптимальний план задачі знайдено. Він має наступний вигляд:
|
|
|
|
Перевіримо правильність виконання поставленої задачі за допомогою MathCad.
Результат виконання поставленої задачі представлений на рисунку 2.1.

Рисунок 2.1 – Вирішення поставленої задачі у MathCad

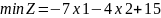
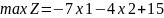
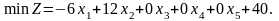
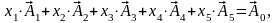
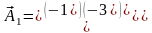 (2.4)
(2.4)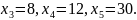
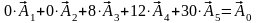
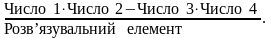 (2.7)
(2.7)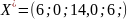 (2.8)
(2.8) (2.9)
(2.9)