
Задача№1. Краткая характеристика моделей объектов управления
 Объект
управления ОУ – это часть среды,
выделенная таким образом, что на ОУ
можно воздействовать и это воздействие
позволяет перевести состояние ОУ в
заданном направлении.
Объект
управления ОУ – это часть среды,
выделенная таким образом, что на ОУ
можно воздействовать и это воздействие
позволяет перевести состояние ОУ в
заданном направлении.
Под моделью понимают зависимость, которая в удобной форме отражает существенные стороны (процессы) реального объекта управления (проектирования).
Модели объектов управления бывают:
- процедурные – для управления объектом;
- производственно-экономические – математические модели, позволяющие вести анализ и планирование производственной деятельности отдельных предприятий, отраслей промышленности и всего народного хозяйства в целом;
- функциональные.
Различают модели
- для целей управления,
- для целей проектирования,
- для прогнозирования,
- для отражения физико-химических процессов, протекающих в объекте,
- для исследования, для диагностики, для классификации, для обучения и т.д.
Модели бывают концептуальные, физические, математические (аналитические) в зависимости от средств их описания.
Независимо от сложности объекта управления его структурная схема может быть представлена в виде (рисунок 1.1).


Рисунок 1.1 - Структурная схема ОУ
Здесь
 -
вектор управляющих воздействий,
-
вектор управляющих воздействий,
 – время;
– время;
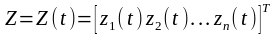 -
вектор контролируемых неуправляемых
воздействий (возмущений);
-
вектор контролируемых неуправляемых
воздействий (возмущений);
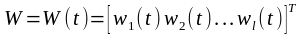 -
вектор неконтролируемых воздействий
(помех и возмущений);
-
вектор неконтролируемых воздействий
(помех и возмущений);
 -
вектор состояния ОУ, содержащий всю
информацию о прошлом ОУ, необходимую
для определения реакции на входные
воздействия;
-
вектор состояния ОУ, содержащий всю
информацию о прошлом ОУ, необходимую
для определения реакции на входные
воздействия;
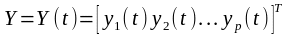 -
вектор наблюдаемых выходных переменных.
-
вектор наблюдаемых выходных переменных.
Зависимость между выходными и входными переменными в общем виде представляется моделью
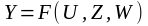 . (1.1)
. (1.1)
Возможная классификация моделей ОУ вида (1.1) приведена на рисунке 1.2.


Рисунок 1.2 - Классификация моделей объектов управления
Если
величины
 непрерывны, то множество
непрерывны, то множество
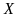 будет бесконечным, но при этом значение
вектора
могут быть ограничены условиями типа:
будет бесконечным, но при этом значение
вектора
могут быть ограничены условиями типа:
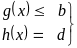
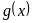 – векторная
функция;
– векторная
функция;
 – векторная
функция;
– векторная
функция;
Набор всех ограничений можно свести:
 .
.
Задача№2. Постановка задач математического программирования
В
задачах статической оптимизации обычно
не рассматривается методы реализации
принятого решения (управления), т.е. не
определяется величина и характер
управляющего воздействия
 ,
а определяется величина, состояние
объектов
,
а определяется величина, состояние
объектов
 ,
которое обеспечивает достижение цели
управления.
,
которое обеспечивает достижение цели
управления.
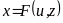 ;
;
 , (2.1)
, (2.1)
где
 – целевая функция.
– целевая функция.
Статическая задача управления предприятием, либо экономика его отрясли, связана с распределением ограниченных ресурсов на управление в определенный момент времени. Но собственно управление во времени как оно будет реализовано нас не волнует.
Общая
задача математического программирования
состоит в поиске вектора
из допустимого множества
,
чтобы обеспечить максимум целевой
функции
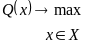 .
.
Характерны 3 задачи математического программирования:
Задача классического математического программирования
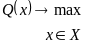 (2.2)
(2.2)
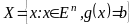
Необходимо
найти максимум целевой функции
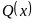 по переменным
,
принадлежащих множеству
,
где множество
есть множество переменных
,
принадлежащих Евклидову пространству
и удовлетворяющих ограничениям типа
равенств g(x),
где:
по переменным
,
принадлежащих множеству
,
где множество
есть множество переменных
,
принадлежащих Евклидову пространству
и удовлетворяющих ограничениям типа
равенств g(x),
где:
 – непрерывно
дифференцируемые функции.
– непрерывно
дифференцируемые функции.
Задача нелинейного программирования:
(2.3)

Задача линейного программирования:
 (2.4)
(2.4)

Целевая функция линейна относительно х – гиперплоскость и ограничения линейны относительно х, в центре пересечения гиперплоскостей они образуют многогранник ограничений.
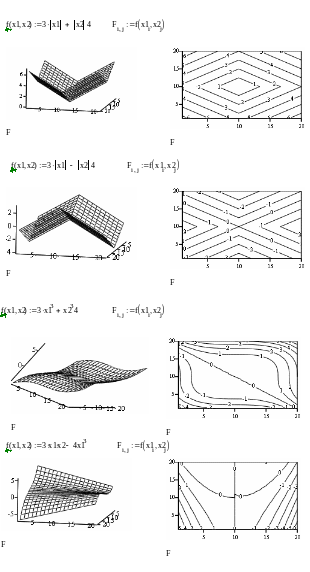
Задача №3. Изобразить на плоскости Е 2 линии равного уровня C
Qc
=
 ,
,
где C = 0, 1, 2, следующих функций f (x1, x2):
а) а x1 + b x2; д) а | x1 | + b | x2|;
б) а x12 + b x22; е) а | x1 | - b | x2|;
в) а x12 - b x22; ж) а x13 + b x23;
г) а x12 + b x2; з) а x1 x2 - b x13:
a=3 b=4


Задача№ 4. Найти точку глобального минимума функции
Q (x) = ax12 + 2x1 x2 + bx22 - 2x1 - 3x2 min
x X ,
где
Х =
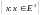 .
.
В
соответствии с вариантом
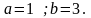

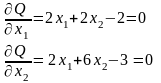



Задача №5. Найти глобальное решение задачи
Q (x) = x1 x23 max
х Х ,
где Х = х: х Е2, ax1 + bx2 = c
а) методом исключения переменных;
б) методом множителей Лагранжа:
=>
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определим
стационарные точки:
=>
=>
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()
Задача №6. Решить задачу математического программирования методом множителей Лагранжа:
Q (x) = x12 + x2 min
x X
X = x: x E2, x1 + x2 = 4.
![]()
![]()
=>
x^*=(0.5;3.5)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача №7. Решить задачу математического программирования методом множителей Лагранжа:
Q (x) = - x12 -2 - x22 + 4 max
x X
X = x: x E2, x1 + x2 = 1.
Найти оптимальное значение Q (x) для ограничения x1 + x2 = 4.
Найти оптимальное значение Q (x) для ограничения x1 + x2 = 4.

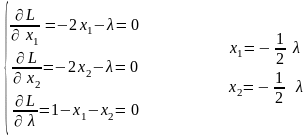
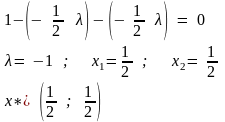
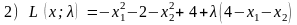


Задача №8. Изобразите на плоскости допустимое множество, заданное системой неравенств:
3х1 + х2 18,
4х1 - ах2 - 24,
bx1 - 12 x2 36,
cx1 + 3 x2 - 27:
В соответствии с вариантом :

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
=>
=>
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
при
![]()
![]()
![]()
![]()
![]()
при
![]()
![]()
![]()
![]()
![]()
при
![]()
![]()
![]()
![]()
![]()
при
![]()
![]()
![]()
![]()
![]()
![]()
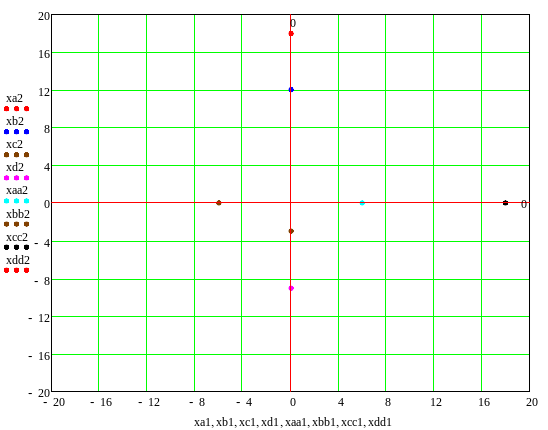

Точка à Точка b Точка c Точка d

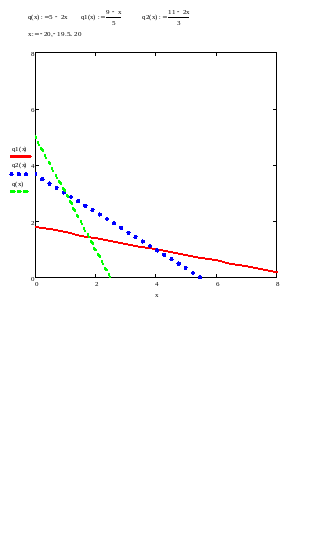
Задача №9. Используя геометрические построения, найти решение задачи линейного программирования:
Q (x) =а х1 + х2 min,
x X ,
где Х = х: х Е2, x1 + ( b - 3) x2 b, (c - 4) x1 + x2 c, 3 x1 + 2 x2 11, x1 0, x2 0
 В соответствии
с вариантом :
В соответствии
с вариантом :

Ограничения:
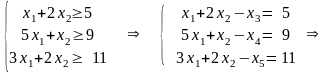
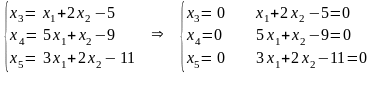



Задача №10.Даны:
а) прямая задача линейного программирования
Q (x) = х1 + 2 х2 - х3 max,
х Х ,
где Х = х: х Е2, - x1 + 4 x2 - 2 x3 a, x1 + x2 + 2 x3 b, 2 x1 - x2 + 2 x3 c, x1 0, x2 0, x3 0;
б) ее допустимые точки (векторы)
х1
=
 ,
x2
=
,
x2
=
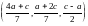 ;
;
с) а также допустимые точки (векторы) двойственной задачи
1
=
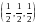 ,
2
=
,
2
=
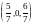
Определить, имеются ли среди этих точек (векторов) решения прямой и двойственной задач:
В соответствии с вариантом :



Так как условие дополняющей нежёсткости не выполняется, следовательно, среди заданных точек векторов решений нет.
Задача №11. Прядильная фабрика для производства двух видов пряжи использует три типа сырья- чистую шерсть, капрон и акрил. В таблице указаны нормы расхода сырья, его общее количество, которое может быть использовано фабрикой в течение года, и прибыль от реализации тонны пряжи каждого вида.
|
Нормы расхода сырья на |
|
||
Тип сырья |
1 т пряжи (т) |
Количество |
||
|
Вид 1 |
Вид 2 |
сырья (т) |
|
Шерсть |
0, 5 |
0, 2 |
600 |
|
Капрон |
а |
0, 6 |
b |
|
Акрил |
0, 5 - а |
0, 2 |
c |
|
Прибыль от реализации |
|
|
|
|
1 т пряжи (р.) |
1100 |
900 |
|
|
Требуется составить годовой план производства пряжи с целью максимизации суммарной прибыли.
В
соответствии с вариантом :

 -количество
пряжи первого вида;
-количество
пряжи первого вида;
 -количество
пряжи второго вида;
-количество
пряжи второго вида;
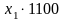 -прибыль
от реализации первого вида;
-прибыль
от реализации первого вида;
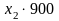 -прибыль
от реализации второго вида;
-прибыль
от реализации второго вида;
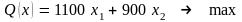

где
Х=
 ;
;

При имеющихся ресурсах максимальную прибыль принесет производство 400 т пряжи первого вида и 1400 т – второго вида.

Задача №12. Нефтеперерабатывающий завод использует две различные технологии перегонки нефти для производства бензина, керосина и солярового масла. В таблице приведены данные, показывающие выход продукции, отходы, издержки производства (стоимость нефти, заработная плата, амортизация и т. п.) и загрузку оборудования в расчете на 1 т переработанной нефти. Кроме того, указаны стоимость 1 т готовой продукции и суточный объем государственного заказа, который необходимо удовлетворить.
|
Выход продукции (т) |
|
|
|
Наименование |
|
|
Стоимость 1 т |
Суточный |
продукции |
Технология 1 |
Технология 2 |
готового продук- |
объем госзака- |
|
|
|
та (р.) |
за (т) |
Бензин |
0, 6 |
0, 3 |
100 |
117 |
Керосин |
0, 1 |
0, 3 |
50 |
54 |
Соляровое масло |
- |
0, 3 |
20 |
|
Отходы |
0, 3 |
0, 1 |
|
|
Издержки произ- |
|
|
|
|
водства (р.) |
а |
b |
|
|
Загрузка обору- |
|
|
|
|
дования (маш.-ч) |
0, 2 |
0, 05 |
|
|
Ресурс оборудования составляет 75 маш. -ч в сутки. Все отходы должны пройти через очистные сооружения, производительность которых составляет с т/сут. Поставки нефти и спрос на всю продукцию завода не ограничены.
Требуется составить суточный план производства с целью максимизации прибыли:
В
соответствии с вариантом :
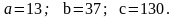
-обьем нефти переработанной по 1-ой технологии;
- обьем нефти переработанной по 2-ой технологии;
 -стоимость
выхода всей продукции;
-стоимость
выхода всей продукции;
 -стоимость
издержек производства;
-стоимость
издержек производства;
Составим ограничения:
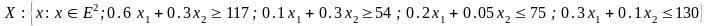

 -суточный
объём заказа бензина;
-суточный
объём заказа бензина;
 -суточный
объём заказа керосина;
-суточный
объём заказа керосина;
 -объём
разгрузки оборудования;
-объём
разгрузки оборудования;
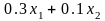 -количество
отходов, пройденных через очистные
сооружения
-количество
отходов, пройденных через очистные
сооружения
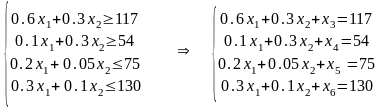


Задача №13. На рисунке показана технологическая схема изготовления детали каждого вида с указанием времени ее обработки на станках. Задан суточный ресурс рабочего времени каждого станка: b мин для станка 1, с мин для станка 2. Стоимость одной детали вида 1, 2 и 3 составляет 3, 1 и 2 р. соответственно. Требуется составить суточный план производства деталей с целью максимизации стоимости выпущенной продукции.
Станок 1 Станок 2

 3
мин 6 мин
Деталь 1
3
мин 6 мин
Деталь 1
З
 аготовки
9 мин
Деталь 2
аготовки
9 мин
Деталь 2

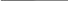
 а
мин
3 мин Деталь 3
а
мин
3 мин Деталь 3
В
соответствии с вариантом :

Составим уравнения:

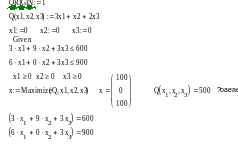
Задача №14. Для производства трех видов изделий ( А, В и С) используется сырье типа 1, 11 и 111, причем закупки сырьё типа 1 и 111 ограничены возможностями поставщиков. В таблице приведены нормы затрат сырья, цены на сырье и на изделия, а также ограничения по закупке сырья.
|
|
|
|
|||
Тип |
Цена 1 кг |
Нормы затрат сырья на одно |
Ограничения |
|||
сырья |
сырья (р.) |
изделие (кг) |
по закупке |
|||
|
|
А |
В |
С |
сырья (кг) |
|
|
|
|
|
|
|
|
1 |
2 |
1 |
3 |
а |
3000 |
|
11 |
1 |
4 |
1 |
3 |
- |
|
111 |
b |
6 |
5 |
2 |
3320 |
|
|
|
|
|
|
|
|
|
Цена одного |
6 b + 12 |
5 b + 22 |
c |
|
|
|
изделия (р.) |
|
|
|
|
|
Требуется определить план производства продукции с целью максимизации прибыли:
В
соответствии с вариантом :

Составим ограничения :
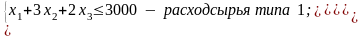
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
Задача №15. Процесс изготовления двух видов изделий заводом требует, во-первых, последовательной обработки на токарных и фрезерных станках, и, во-вторых, затрат двух видов сырья: стали и цветных металлов. Данные о потребности каждого ресурса на единицу выпускаемого изделия и общие запасы ресурсов помещены в таблице.
|
Затраты на 1 изделие |
Ресурсы |
||
А |
В |
|||
Материалы |
Сталь (кг) |
10 |
70 |
320 |
Цветные металлы(кг) |
20 |
50 |
420 |
|
Оборудование |
Токарные станки (станкочасов) |
300 |
400 |
6200 |
Фрезерные станки (станкочасов) |
200 |
100 |
3400 |
|
Прибыль на изделие ( в тыс. руб.) |
3 |
8 |
|
|
Прибыль от реализации единицы изделия А-3 тыс. рублей, единицы изделия В- 8 тыс. рублей. Определить такой план выпуска продукции, который обеспечивает максимальную прибыль при условии, что время работы фрезерных станков должно быть использовано полностью.
-количество изделий А
-количество изделий В
Запишем ограничения:

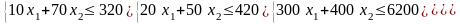
Составим функцию:
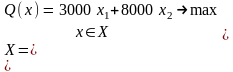
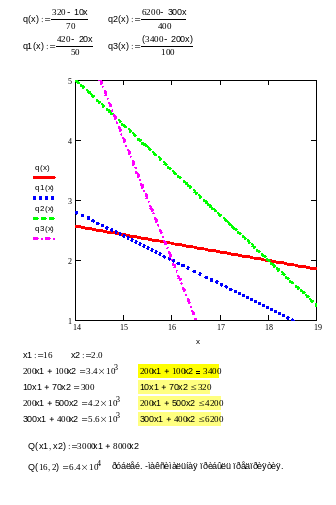
Задача №16. Заводу требуется составить оптимальный по реализации производственный план выпуска двух видов А и Б изделий при определенных возможностях четырех видов машин. План выпуска должен быть таким, чтобы от реализации выпущенной по этому плану продукции завод получил бы наибольшую прибыль. Оба вида изделий последовательно обрабатываются этими машинами. План должен учитывать, что 1-й вид машин ежедневно может обрабатывать эту продукцию в течение 18 часов, 2-й - 12 часов, 3-й – 12 часов, 4-й - 9 часов. В таблице указано время, необходимое для обработки каждого изделия этих двух видов изделий указанными типами машин. Нуль означает, что изделие машинами данного вида не обрабатывается. Завод от реализации одного изделия вида А получает 4 рубля, а от реализации одного изделия вида Б-6 рублей прибыли.
Виды машин |
|
|
|
|
|
1-й |
2-й |
3-й |
4-й |
Виды изделий |
|
|
|
|
|
|
|
|
|
А |
1 |
0, 5 |
1 |
0 |
|
|
|
|
|
Б |
1 |
1 |
0 |
1 |
Возможное время |
|
|
|
|
работы машин (час) |
18 |
12 |
12 |
9 |
|
|
|
|
|
