Взаимное влияние местных сопротивлений

Принцип наложения потерь напора, применяющийся в гидро­аэромеханике, заключается в том, что суммарные потери напора от ряда местных сопротивлений определяются простым сложением потерь напора от каждого сопротивления в отдельности. Для этого местные препятствия должны находиться на таких расстояниях друг от друга, чтобы на проявление потерь данного местного пре­пятствия не влияли соседние. При этом деформации потока, вы­званные данным местным сопротивлением, полностью исчезают до взаимодействия потока с последующим соседним сопротивлением, т. е. поток стабилизируется до взаимодействия с последующим сопротивлением.

Для трубопроводов под длиной участка стабилизации l пони­мается такая длина прямого участка трубопровода после местного сопротивления, на котором полностью затухает возму­щение потока от этого местного сопротивления. В общем случае длина / зависит в первую очередь от вида местного сопротивления и режима движения (числа Re). При расстояниях между мест­ными сопротивлениями l и более их взаимное влияние не прояв­ляется. Обычно длина участка стабилизации находится в диапа­зоне l= (30-60)d. Имеются приближенные формулы для оценки значений /.

При близком расположении местные сопротивления взаимо­действуют друг с другом, так что принцип прямого сложения потерь напора недопустим. Здесь каждое из расположенных далее по течению сопротивлений взаимодействует с еще не стабилизи­ровавшимися потоками от предыдущего сопротивления. Вопрос о взаимном влиянии близко расположенных сопротивлений в отно­шении потерь напора еще не достаточно изучен, хотя некоторые результаты достигнуты. Общие потери напора от близко распо­ложенных ряда местных сопротивлений в общем случае не равны простой сумме частных потерь от отдельных сопротивлений. Сум­марный коэффициент сопротивления может быть меньше или больше простой арифметической суммы частных коэффициентов. В большинстве случаев суммарный коэффициент сопротивления меньше арифметической суммы частных коэффициентов. Поэтому применяющееся часто на практике прямое суммирование потерь напора от местных сопротивлений увеличивает общие потери, что дает некоторый запас. Вместе с тем следует иметь в виду, что суммарные потери напора могут быть больше простой суммы част­ных потерь (при близком размещении отдельных видов местных сопротивлений).

Сложение путевых и местных потерь напора.

Коэффициент сопротивления системы

Гидравлическая система на рис. 6.5 включает состоящий из двух участков трубопровод с рядом местных сопротивлений: во­дозаборное устройство с коэффициентом сопротивления ksi₃аб; вне-

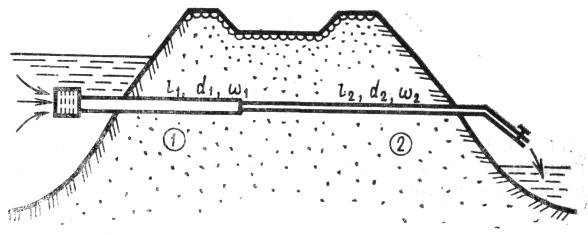
Рис. 6.5

запное сужение (ksi_вн. _с); поворот (ksi_Пов); кран (ζ_κρ). Первый уча­сток трубопровода характеризуется длиной l₁ внутренним диамет­ром d1, площадью живого сечения w1 и средней скоростью пото­ка v₁. Второй участок имеет параметры l₂, d₂, w₂, V₂. Так как (w1>w2, то v1<v₂. Режим движения в трубопроводе развитый тур­булентный, течение установившееся. Необходимо составить выра­жение для общих потерь напора h_w в системе.

Для определения путевых и местных потерь в системе необ­ходимо использовать формулы (6.11), (6.26). Тогда, представляя общие потери hw как сумму путевых hf и местных hj, следует

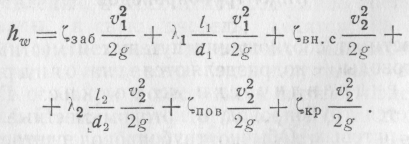
Связь скоростей υ1 и V₂ из уравнения неразрывности движения V1w1 = V₂w2 следует в виде ν1 = ν₂(ω₂/ω1). С учетом этого, а также вынося за скобки скоростной напор v²₂/2g, последнее выражение преобразуется к виду

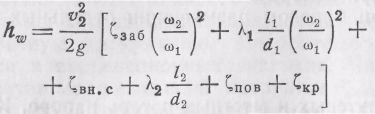
или окончательно

(6.38)

где коэффициент сопротивления системы

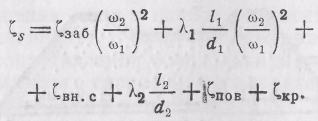(6.39)

Очевидно, что аналогичные выражения для ζ_s различных дру­гих гидравлических систем можно составлять непосредственно без написания промежуточных выражений.