13.5 Зависимость аэродинамических коэффициентов

ОТ ЧИСЛА Re, СТЕПЕНИ ТУРБУЛЕНТНОСТИ ПОТОКА

И ФОРМЫ ПРОФИЛЯ

Для данного профиля при неизменных числах Μ степени тур­булентности потока ε, угле атаки а коэффициент минимального лобового сопротивления в значительной степени зависит от чи­сел Рейнольдса. У профилей средних относительных толщин (с=10... 15%) с увеличением числа Рейнольдса с_{ya mаx} увели­чивается. При небольших значениях чисел Re величина коэффи­циента Суa max обусловлена отрывом ламинарного пограничного слоя. С увеличением числа Re точка перехода ламинарного по­граничного слоя в турбулентный обычно смещается вверх по течению и, следовательно, происходит отрыв уже турбулентного пограничного слоя. Зона срыва при этом уменьшается и коэф­фициент c_{ya max} увеличивается.

У тонких профилей (с = 5... 6%) и профилей с заостренным носиком коэффициент С_{ya max} с изменением числа Re остается почти постоянным, так как отрыв потока у тонких профилей про­исходит вблизи передней кромки профиля и при малых углах атаки.

У очень толстых профилей (с=15... 20%) коэффициент cya max обычно невелик и с увеличением чисел Re уменьшается, так как в кормовой части таких профилей уже при малых углах атаки возникают большие градиенты давления, приводящие к более раннему отрыву пограничного слоя.

Коэффициент минимального лобового сопротивления c_{xa min} определяется коэффициентом трения плоской пластины С_f, кото­рый, в свою очередь, зависит от числа Рейнольдса: Cf~l/Reⁿ, где n=0,5 для ламинарного и n = 0,2 для турбулентного погра­ничного слоя.

Очевидно, что с увеличением числа Re уменьшается коэффи­циент минимального лобового сопротивления.

С возрастанием начальной степени турбулентности потока коэффициент С_{xa min} увеличивается, коэффициент С_{ya max} тонких и толстых профилей изменяется незначительно; коэффициент C_{ya mах} у профилей средних толщин увеличивается. Такое влия­ние начальной турбулентности потока на аэродинамические ха­рактеристики профиля объясняется изменением положения точки перехода ламинарного пограничного слоя в турбулентный с увеличением начальной степени турбулентности.

Рис, 13.9, Изменение коэффициента C_{ya max} в зависимости от кривиз­ны f и абсциссы x_f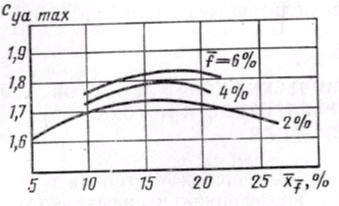

С ущественное влияние на аэродинамические коэффициенты профиля оказывают геометрические параметры профиля. С уве­личением относительной тол­щины профиля происходит увеличение коэффициента ми­нимального лобового сопротив­ления Сxа min. Коэффициент максимальной подъемной силы с_уa max с возрастанием увеличивается, а в диапазоне 12—20% -уменьшается. Влияние на коэффи­циент максимальной подъемной силы Cya max дозвукового профиля большой относитель­ной толщины показано на рис, 13-9.

С увеличением относительной кривизны профиля f коэффици­ент c_{xa min} (у профилей средних толщин), коэффициент с_т и угол нулевой подъемной силы (по абсолютной величине) возрастают.

13.6. Центр давления. Фокус профиля

1. Условимся аэродинамические характеристики цилиндрическо­го крыла с заданным профилем в условиях плоскопараллельного обтекания невозмущенным потоком всех его сечений, назы­вать характеристиками профиля крыла.

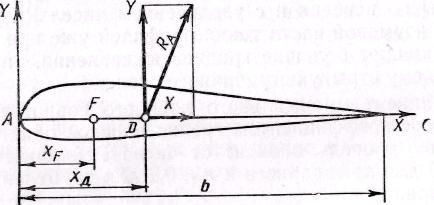
Рис. 13.10, К определению центра давления и фо­куса профиля

Точка D, являющаяся точкой пересечения линии действия полной аэродинамической силы с хордой крыла, называется центром давления (рис. 13. 10). Отношение абсциссы центра данления к хорде профиля обозначается через хд=х_Д/b. Для опре­деления абсциссы точки приложения аэродинамической силы нужно знать момент аэродинамической силы относительно какой-либо точки на профиле (например, относительно передней кром­ки профиля).

Момент нормальной силы относительно передней кромки про­филя можно записать в виде

M_z= - Y x_д = -(Y_a cos α + X_a sin α) x_д, (13.18)

откуда находится абсцисса центра давления, отсчитываемая от передней кромки профиля: (13.19)

Используя же выражения (13.8), (13.9), (13. 17), получим

(13.20)

Опыты показывают, что в значительной степени для тонких и слабоизогнутых профилей величины С_ya и m почти не зависят от формы профиля, а С_м0 наоборот в значительной степени зависят от формы профиля.

Момент силы Υ относительно произвольной точки F на хорде профиля (см. рис. 13.10) М_F = – Y (х_Д —X_F) = M_z + Yx_F.

Переходя от размерных величин к коэффициентам и учиты­вая (13. 7), получим

C_mF = C_m + C_y x_F = c_m0 + m C_y + C_y x_F = C_m0 + ( m + x_F ) C_y. (13.21)

Очевидно, что при х_F = – m коэффициент момента c_mf =c_m0 и не зависит от угла атаки. Характерная для профиля точка F, обладающая тем свойством, что вычисленный относительно нее главный момент сил давления потока не зависит от угла атаки, называется фокусом крыльевого профиля.

Для большинства профилей при малых числах Μ (т.е. без учета сжимаемости) коэффициент m = -0,22...-0,25. Это оз­начает, что х_F = -m = 0,22...0,25 или x_F = (0,22...0,25)b т.е. фокус профиля крыла находится примерно на расстоянии 1/4 хорды от передней кромки. Неизменное положение фокуса на хорде возможно лишь при линейной зависимости c_m = f(c_ya).Для симметричного профиля кривые c_m= f(a) и с_уa = f(а) проходят через начало координат. В таком случае в пределах линейной зависимости из двух треугольников (рис. 13.11) по­лучим: – С_m = a₁ tg ₁ С_ya = a₁ tg ₂ (13.22)

(13.23)

Следовательно, для симметричного профиля положение цент­ра давления по углам атаки остается неизменным и совпадает с фокусом профиля

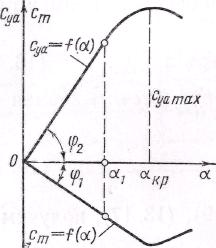
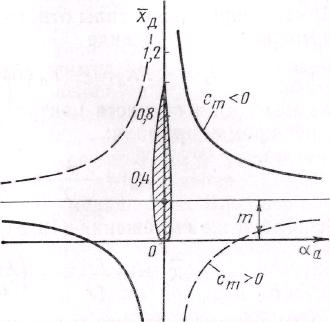
Рис.13.11 Изменение аэродинамических коэф­фициентов c_yα и с_т в за­висимости от угла атаки α в случае симметрич­ного профиля

Рис. 13,12. Изменение коэффициента

центра давления в зависимости от

аэродинамического угла атаки

Центр давления несимметричного профиля с изменением уг­ла атаки перемещается вдоль хорды или ее продолжения от минус бесконечности до плюс бесконечности (рис. 13, 12), Гра­фически зависимость х_Д от аэродинамического угла атаки а_а изображается равнобочной гиперболой. В случае с_m<0 {сплошная линия) центр дав­ления с возрастанием угла атаки 'перемещается к носику профиля, а в случае с_m>0

( пунктирная линия) — к хвостику.

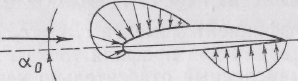
Рис. 13.13. Распределение аэродина­мической нагрузки по профилю при угле нулевой подъемной силы a₀

При α = α₀ (что соответствует с_уа=0) центр давления нахо­дится на бесконечности, так как при отсутствии подъемной силы аэродинамическое воздействие на такой профиль приводится к паре сил (рис. 13. 13).