Лекция по теме

ПРОФИЛЬ КРЫЛА

Аэродинамика крыльев, оперений и других близких к ним по форме и назначению частей летательных аппаратов в большой мере определяется формой их сечений в направлении обтекающего потока или так называемой формой профиля. И несмотря на то, что сам профиль не является отдельной деталью летательного аппарата, его изучение тем не менее представляет интерес. В чистом виде аэродина­мика профиля рассматривается как аэродинамика сечения прямого крыла бесконеч­ного размаха.

Профили, используемые при аэродинамической компоновке крыльев и опере­ний, по своим геометрическим и аэродинамическим характеристикам могут весьма существенно различаться в зависимости от особенностей тех задач, которые призваны решать соответствующие летательные аппараты.

Аэродинамические характеристики профилей крыльев и оперений должны обеспечивать летательному аппарату при заданной подъемной силе наименьшее сопротивление и необходимую устойчивость и управляемость на всех режимах по­лета (в том числе и на околокритических углах атаки, при которых отдельные участки крыла или оперения могут обтекаться в условиях отрыва потока от их поверхности). Для аппаратов с большой дальностью полета профили крыльев должны обладать еще и высоким значением аэродинамического качества на соответству­ющих этому полету значениях с_уа. Помимо отмеченных обычно возникает ряд до­полнительных требований, предъявляемых к профилю. К таким требованиям, в пер­вую очередь, следует отнести необходимость снижения величины момента тангажа при подъемной силе, равной нулю, обеспечение эффективности элеронов и рулей, расположенных на крыле или оперении и др. Кроме того, к геометрическим пара­метрам профиля могут предъявляться требования, связанные с конструкцией, проч­ностью и особенностями технологии (объемы, строительные высоты и пр.). Есте­ственно, что все эти требования иногда являются весьма противоречивыми, поэтому развитие профилей сопровождается большой их специализацией.

Следует иметь в виду, что выбор профилей и аэродинамической компоновки крыла или оперения является взаимосвязанным процессом, так как, с одной сто­роны, удовлетворение заданных требований может достигаться как за счет свойств самого профиля, так и за счет формы крыла или оперения, а с другой стороны, выбор тех или иных профилей самым существенным образом зависит от необходимой формы крыла или оперения в связи с теми задачами, которые должен решать лета­тельный аппарат. Так например, в соответствии с тем, на каких скоростях (дозвуко­вых, трансзвуковых, сверхзвуковых или гиперзвуковых) и углах атаки протекают основные режимы полета летательного аппарата, формируется его аэродинамическая компоновка и выбираются формы и размеры отдельных частей, таких как формы несущих и управляющих поверхностей и их профилей. В частности, в корневых отсеках прямых и стреловидных крыльев, как правило, не могут использоваться одинаковые профили. Это связано с тем, что вследствие различных условий обтека­ния, профиль, пригодный для прямого крыла, оказывается непригодным для стрело­видного крыла. В области крыла, обслуживаемой элеронами, и для оперения целесо­образны специальные профили, позволяющие сохранять эффективности элеронов или рулей и благоприятное изменение шарнирных моментов.

Для обеспечения без­опасности полета самолетов с крыльями обычных и больших удлинений может при­меняться набор профилей по размаху, имеющих различную форму. При этом кон­цевые профили выбираются с большими значениями С_{уа mах} , чем корневые профили. Обеспечение скоростных характеристик летательных аппаратов, совершающих полет в области трансзвуковых скоростей, обычно достигается путем увеличения значения критического числа М_кр всего аппарата и, в частно­сти, профилей его крыла. Для этой цели применяются профили специальной формы, создающие минимальные возмущения по­тока.

Обеспечение малого сопро­тивления летательных аппара­тов, совершающих полет только при сверхзвуковых скоростях, обычно достигается за счет при­менения тонких заостренных профилей. Во всех этих случаях основной трудностью выбора профилей является необходимость сочетания высоких скоростных и несущих свойств.

Имеются расчетные методы, которые под заданные аэродинамические характе­ристики позволяют определять (с последующей экспериментальной проверкой) соответствующие геометрические параметры профиля и в конечном итоге коорди­наты его контура. Накопленные расчетные и экспериментальные данные позволяют создавать профили, отвечающие самым разнообразным требованиям, в том числе и с узко направленными свойствами.

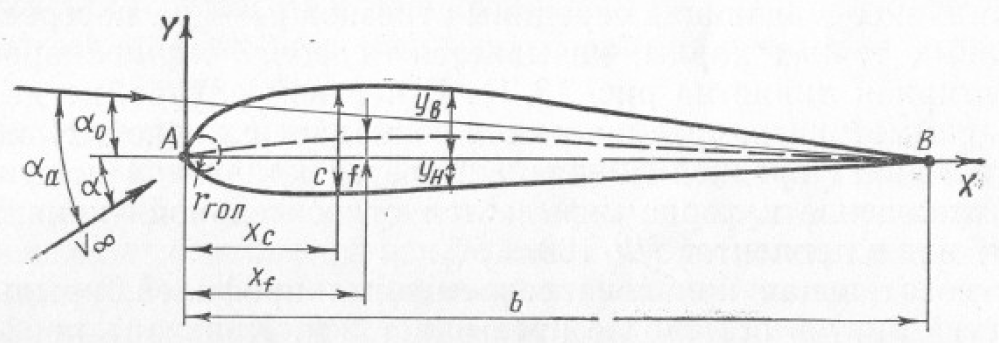
Рис. 1.1. Схема геометрических параметров профиля

На рис. 1.1 приведена схема профиля с указанием основных геометрических параметров, которые оказывают наиболее существенное влияние на аэродинами­ческие характеристики. Обычно при описании геометрических характеристик про­филя пользуются прямоугольной системой координат, у которой начало распола­гается в передней точке (носике) профиля, а ось ОХ проходит через заднюю (хвосто­вую) точку профиля. Ось OY направлена вверх. В этой системе координат уравнения верхнего и нижнего контуров профиля соответственно записываются в виде

у_верх = f₁(x), у_ниж = f₂(x) (1.1)

При этом приняты следующие названия и обозначения основных геометрических параметров.

Хорда профиля b — линия, соединяющая две наиболее удаленные точки про­филя, т. е. переднюю и заднюю его точки. Хорда разделяет контур профиля на две части – верхнюю и нижнюю. Исключение составляют только сильно изогнутые профили, у которых часть контура может оказаться расположенной по одну сторону хорды профиля.

Угол атаки α – угол между хордой профиля и направлением проекции вектора скорости невозмущенного потока на плоскость профиля.

Толщина профиля с— расстояние между точками контура профиля, лежащими на перпендикуляре к хорде, с = |у_верх| + |у_ниж|.

Максимальная толщина профиля с_мах— наибольшее расстояние между точками профиля, лежащими на перпендикуляре к его хорде.

Относительная толщина профиля — отношение максимальной толщины про­филя к его хорде, выраженное в процентах

Средняя линия профиля — линия, соединяющая середины отрезков |y_верх| + |y_ниж|. перпендикулярных хорде в различных ее точках.

Кривизна профиля f — наибольшая ордината средней линии. Относительная кривизна профиля — отношение максимальной кривизны профиля к его хорде, выраженное в процентах

Относительная кривизна современных профилей крыльев и лопастей винтов обычно не превышает 2%. Кривизна профилей самолетов 20-30х годов доходила до 6-8 %.

Абсциссы наибольшей толщины профиля и наибольшей кри­визны соответственно обозначаются х_c и х_f (см. рис. 1. 1). От­ношения этих величин к хорде носят названия относительных абсцисс соответственно толщины и кривизны: x_c = x_c/b, xотнf = х_f /b. Значения х_сотн у дозвуковых профилей колеблются в пределах 25—30%, у сверхзвуковых 40—50%.

Радиусы кривизны в «носике» и «хвостике» профиля r_н и r_хв ·— радиусы окруж­ностей, вписанных в носовой и хвостовой частях контура профиля.

Обычно профили имеют свои обозначения в различных странах. В большинстве случаев в обозначение профиля входит сокращенное название организации, создавшей профиль, и ряд значений геометрических параметров профиля и, в первую очередь, его относительная толщина. В названии некоторых отечественных профилей перед их цифровым обозна­чением введены буквенные обозначения, состоящие из первых букв фамилии авторов, создавших эти профили.

В качестве примера можно привести обозначения профилей, принятые в США. Обозначение профиля содержит название организации, которая разработала про­филь - NACA, с последующими цифрами, обозначающими основные геометрические характеристики профиля. Для четырехзначных профилей NACA (например, NACA-2412) цифровые индексы обозначают следующее: 1-я цифра — кривизну в процентах хорды, 2-я цифра — координату наибольшей кривизны в десятых долях хорды, 3-я и 4-я цифры — толщину в процентах хорды. Для пятизначных профилей NACA (например, NACA 23012) 1-я цифра является мерой кривизны, 2-я цифра — удвоенная величина координаты наибольшей кривизны в десятых долях хорды профиля, 3-я цифр а» указывает на форму средней линии (0 — без точки перегиба, 1 — с точкой перегиба), 4-я и 5-я цифры — толщина в процентах хорды. Для шести­значных профилей NACA (например, NACA 66₂-415) 1-я цифра — принадлежность к серии, 2-я цифра — положение максимума скоростей в десятых долях хорды, 1-я цифра после дефиса — удесятеренная величина максимального коэффициента подъемной силы (мера кривизны), 2-я и 3-я цифры после дефиса — толщина в про­центах хорды.

Из приведенного следует, что в системах обозначения профилей могут исполь­зоваться не только геометрические параметры, но и некоторые аэродинамические величины в зависимости от того, с каких позиций разрабатывался профиль [43].

Серии профилей можно получить путем деформации какого-либо исходного профиля по заданному закону с сохранением не­изменными одного или нескольких перечисленных выше безраз­мерных параметров. Если для мало специализированных профилей представляется возможным про­стым пропорциональным пересчетом образовывать серии различной толщины и во­гнутости, то при большой специализации профили, как правило, нельзя изменять путем пропорционального изменения всех ординат. Для каждого значения толщины и вогнутости имеется своя оптимальная форма профиля, обеспечивающая наиболее благоприятное сочетание скоростных и несущих характеристик.

13.2. Аэродинамические силы и момент

Взаимодействие между газом (воздухом) и движущимся в нем крылом приводит к возникновению непрерывно распреде­ленных по всей поверхности крыла так называемых аэродинами­ческих сил, которые могут быть охарактеризованы величинами нормального ρ и касательного  напряжений в каждой точке поверхности крыла.

Результирующая сил давления и трения, возникающих при движении летательного аппарата относительно воздушной среды, сила , называется полной аэродинамической силой. Часто под полной аэродинамической силой понимают только ре­зультирующую нормальных сил, пренебрегая при этом силами трения.

Момент полной аэродинамической силы относительно перед­ней кромки крыла M_z называется продольным моментом или аэродинамическим моментом тангажа. Момент М_г считается по­ложительным, если он стремится повернуть крыло в сторону уве­личения угла атаки а, и отрицательным – в обратную сторону. Положительный момент называется кабрирующим, а отрица­тельный – пикирующим.

При теоретическом и экспериментальном исследованиях си­лового взаимодействия движущегося тела с окружающей его средой обычно рассматривается не результирующая сила R_A, а проекции этой силы на оси той или иной системы координат, которая выбирается в зависимости от условий задачи. В аэроди­намике чаще используются две системы координат: скоростная и связанная.

В скоростной системе координат ось ОХ_а совпадает с направ­лением скорости полета, ось OY_a перпендикулярна к оси ОХ_а и лежит в плоскости симметрии летательного аппарата. Ось ОZ_a составляет с осями Ох_а и ОУ_a правую систему координат (на­правлена вдоль правого крыла). При аэродинамических расчетах начало координат обычно совмещают с передней кромкой крыла.

В связанной системе координат ось ОХ направлена вдоль хорды крыла или продольной оси самолета, ось ΟΥ перпендику­лярна оси ОХ и лежит в плоскости симметрии летательного ап­парата, ось ΟΖ составляет с осями ОХ и ΟΥ правую систему. В скоростной системе координат проекции силы R_А обозна­чаются Х_а, Υ _а, Z_a, а в связанной Χ, Υ, Ζ (рис. 13.2). При рассмотрении плоских течений аэродинамическая сила раскладывается на две составляющие Х_а, Υ_α (Χ, Υ).

или (13.1)

В скоростной системе координат проекция силы R_A на на­правление, перпендикулярное к скорости невозмущенного пото­ка, называется аэродинамической подъемной силой Y_a , а проек­ция силы ra на направление, противоположное движению кры­ла (самолета), называется лобовым сопротивлением Х_а.

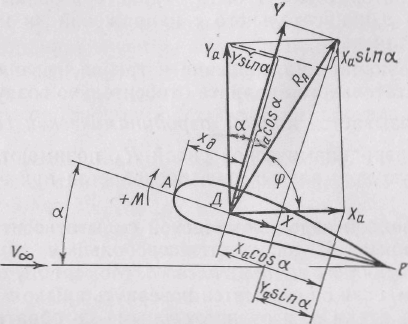
Рис. 13.2. Составляющие полной аэродинами­ческой силы

в скоростной и связанной систе­мах координат

В связанной системе координат силы У и X называются аэродинамической нормальной и продольной силами соответст­венно.

Составляющие силы в этих двух системах координат связа­ны между собой следующими зависимостями (см. рис, 13.2):

Y = Y_асоs  + X_a sin ; Х = Х_а cos  — Y_а sin  (13.2)

или Y_a = Ycos — X sin ; X_a = X cos  + Y sin  (13.3)

Рассмотрим силы, действующие на цилиндрическое крыло бесконечного размаха, обтекаемое потоком жидкости, в связан­ной системе координат, начало которой находится на расстоянии х_с от передней кромки крыла (рис. 13.3). Выделим в качестве характерной длины отрезок крыла длиной l и характерной пло­щади – площадь S=lb (b – длина хорды).

Сила давления, действующая на элемент поверхности крыла ldS равна pldS, а проекции этой силы на оси ОХ и OY: dY = pcosldS = ± lpdx; dX = plsindS = lpdy.

Для определения сил X и Υ необходимо просуммировать эле­ментарные составляющие по всему контуру профиля. Вдоль оси ОХ суммирование производим отдельно для верх­ней и нижней частей профиля, вдоль оси О У — для передней и задней. Тогда для нормальной и продольной сил получим:

где р_п, р_э, р_н, р_в – соответственно давление на передней, задней, нижней и верхней частях профиля.

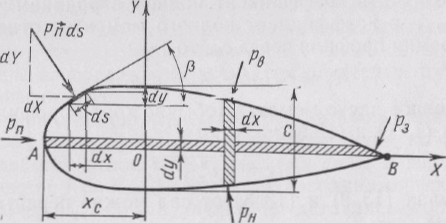
Рис. 13.3. К расчету подъемной силы и лобового сопротивления

Действительная аэродинамическая продольная сила будет больше расчетной на величину равнодействующей сил трения на поверхности крыла. По величинам Y и X для каждого угла атаки с помощью фор­мул связи (13.3) можно определить подъемную силу Y_а и силу лобового сопротивления Х_а.

По опытным данным продольная сила X и толщина профиля малы по сравнению с нормальной силой Y и хордой профиля, поэтому моментом от продольной силы ввиду его малости обыч­но пренебрегают. Зная элементарный момент от нормальной силы

dM_z = – dYx = – ( р_н – р_в)lxdx,

можно определить и полный момент крыла относительно пе­редней кромки профиля

(13.6)