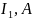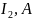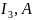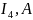4) Трехфазные электрические цепи переменного тока.

Трехфазная система применяется во всем мире для передачи и распределении энергии, что позволяет создать надежные в работе и простые по устройству электродвигатели, генераторы и трансформаторы. Трехфазная система ЭДС – это система трех переменных ЭДС одинаковой частоты и сдвинуты друг относительно друга по фазе так, что сумма трехфазных углов равна 2π или 360^о. Трехфазная система применяется во всем мире для передачи и распространения энергии.

Отдельные обмотки трехфазного приемника называют фазами. При соединении звездой в точках перехода фазные и линейные токи одинаковы между собой в каждой фазе:

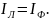
При соединении треугольником обмотки генератора образуют замкнутый контур, в котором действует сумма трех ЭДС:

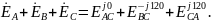
5) Переходные процессы в электрических цепях.

Переходные процессы возникают в электрических цепях при различных коммутациях и других воздействиях, т.е. воздействиях, приводящих к изменению режима работы цепи.

Отметим, что физической причиной возникновения переходных процессов цепях является наличие в них индуктивных и емкостных элементов. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменятся скачком при коммутации в цепях.

Как и при расчете установившихся режимов, для расчета переходного процесса в электрической цепи необходимо все входящие в нее электрические устройства представить соответствующими моделями, т.е.схемами замещения, которые содержат резистивные, емкостные и индуктивные элементы, источники ЭДС и тока, а также коммутационные ключи.

Режим в цепи в течении переходного процесса описывается дифференциальными уравнениями, в общем случае неоднородными ( если в цепи есть источников ЭДС и тока) или однородными (если в цепи нет источников ЭДС и тока). Заметим, что переходной процесс в линейной описывается линейными дифференциальными уравнениями, а в нелинейной – нелинейными.

ВГПК 390202. К13. 021 ПЗ

6

Резисторы

С1- 4 – 0,5 –64 Ом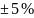

С1-4 – 0,5 –48 Ом

С1-4 – 0,5 –32 Ом

С1-4 – 0,5 – 25 Ом

С1-4 – 0,5 – 51 Ом

С1-4 – 0,5 – 15 Ом

R1

R2

R3

R4

1

1

1

1

1

1

R5

R6

ВГПК 390202. К13. 021 Э3

Линейные электрические цепи постоянного тока

Схема электрическая принципиальная

Савельев

Плюто

Воронцова

7

Воронцова

Группа ВР-33

3. Расчетная часть

1) Расчет линейных электрических цепей постоянного тока

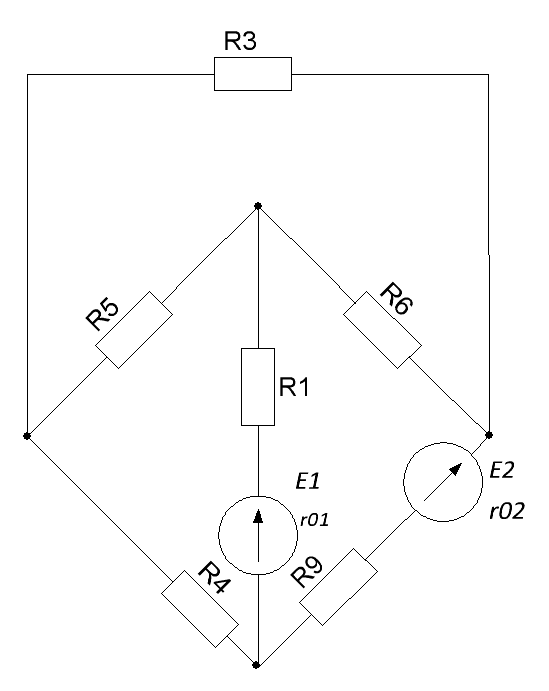
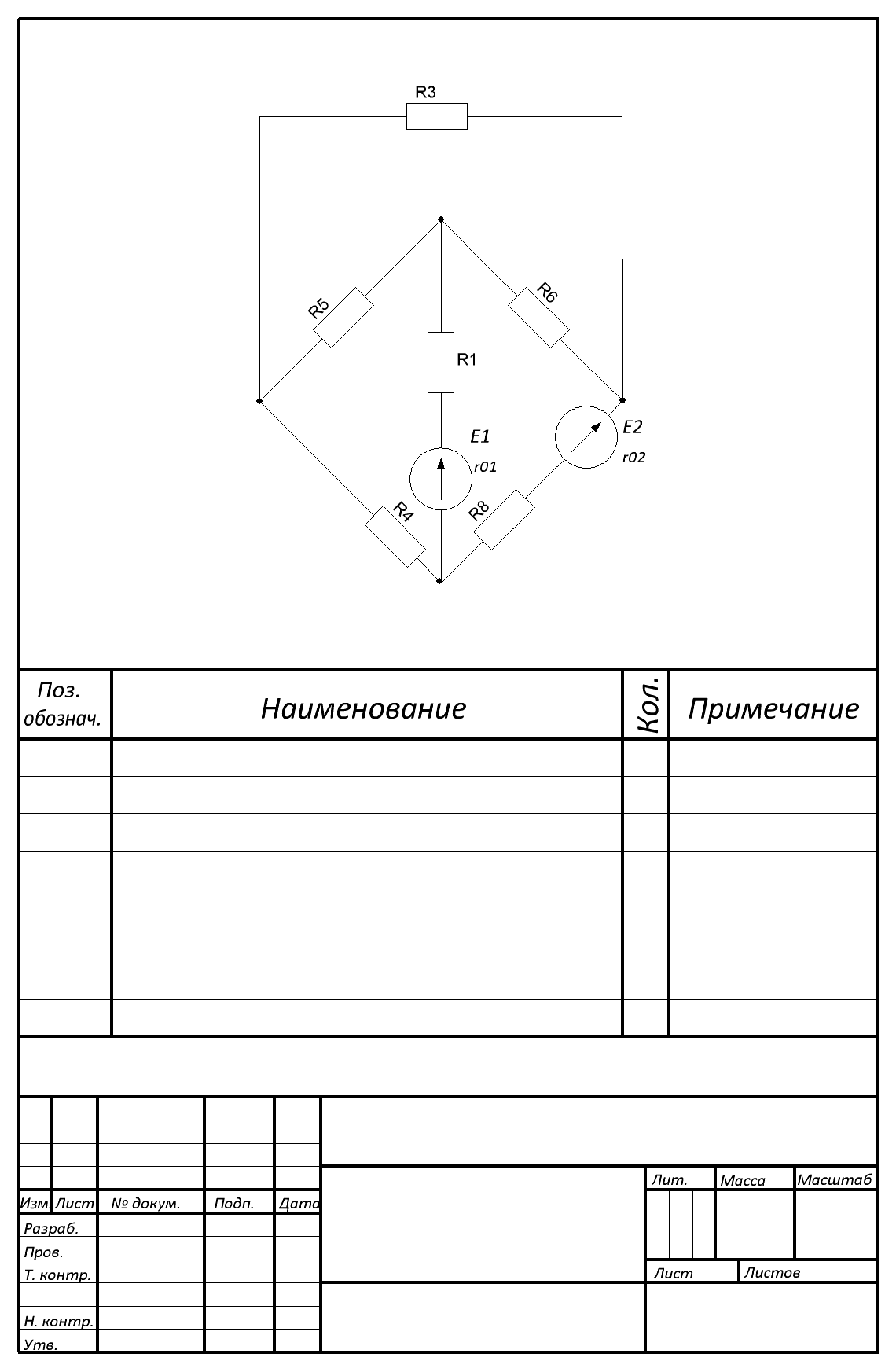
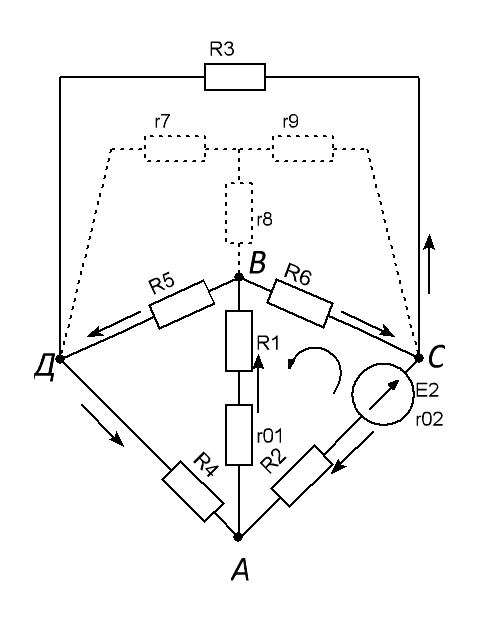
1. Метод узловых и контурных уравнений.

При расчете данным методом произвольно задаем направление токов в ветвях 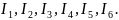На основании 1-ого и 2-ого законов Кирхгофа составляем систему уравнений. Уравнений должно быть столько , сколько в цепи неизвестных токов, то есть для данной схемы . Сначала составляем уравнения для узлов по первому закону Кирхгофа, так как в цепи четыре узла (А,В,С,Д) значит числа уравнений три. Составляем три уравнения для любых 3-х узлов.

Узел С:

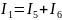
Узел В:

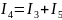
Узел Д:

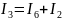
На основании 2-ого закона Кирхгофа составляем три недостающих уравнений:

Контур АСДА– обход по часовой стрелке.

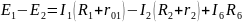
Контур АВСА – обход по часовой стрелке.

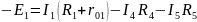
Контур ДСВД – обход по часовой стрелке.

+

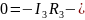
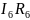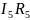
ЭДС в контуре берется со знаком "+", если направление ЭДС совпа­дает с обходом контура, если не совпадает - знак "-".

Падение напряжения на сопротивлении контура берется со знаком «+», если направление тока в нем совпадает с обходом контура , со знаком «-», если не совпадает.

I₃

Дано:

E₁=20В, Е₂=40В,

R₁=64 Ом, R₂=48 Ом,

R₃=32 Ом, R₄=25 Ом,

R₅=51 Ом, R₆=15 Ом,

r₀₁=1 Ом, r₀₂=2 Ом

Определить:

Дано:

E₁=30В, Е₂=20В,

R₁=54 Ом, R₂=42 Ом,

R₃=23 Ом, R₄=31 Ом,

R₅=16 Ом, R₆=51 Ом,

r₀₁=1 Ом, r₀₂=2 Ом

Определить:

С

С

I_k3

I₆

I₅

I₁

I_k1

Д

Д

В

В

I_k2

I₄

I₂

А

А

ВГПК 390202. К13. 021 ПЗ

ВГПТ 390202. К08. 019 ПЗ

8

8

Мы получили систему из шести уравнений с шестью неизвестными:

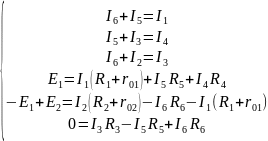
Если при решении системы ток получается со знаком "-", значит его действительное направление обратно тому направлению, которым мы за­дались.

2 .Для определения токов во всех ветвях используем метод контурных токов, который основан на использовании второго закона Кирхгофа. В заданной цепи можно рассмотреть три контура-ячейки и ввести для них контурные токи

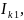
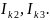
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются на­пряжения на сопротивлениях, входящих в этот контур, а также учитывает­ся падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

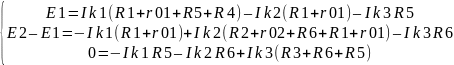
Подставляем в контур численные значения ЭДС и сопротивлений.

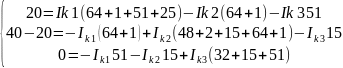
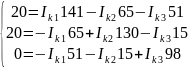
Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители

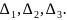
𝛥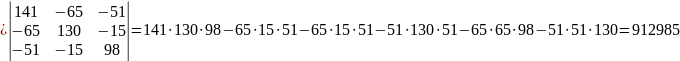

ВГПК 390202. К13. 021 ПЗ

9

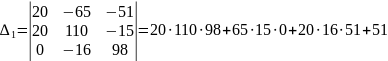
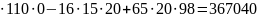
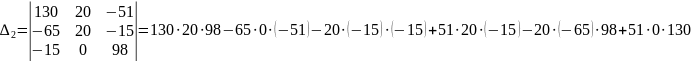=393000

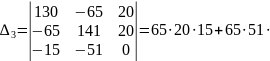20 +

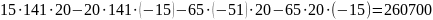
Вычисляем контурные токи:

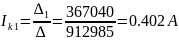
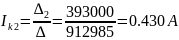
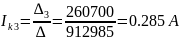
Действительные токи ветвей:

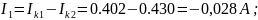
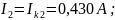
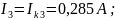
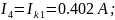
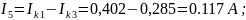
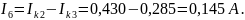
ВГПК 390202. К13. 021 ПЗ

10

3. Метод наложения.

Определяем частные токи от ЭДС E₁, при отсутствии ЭДС E₂.

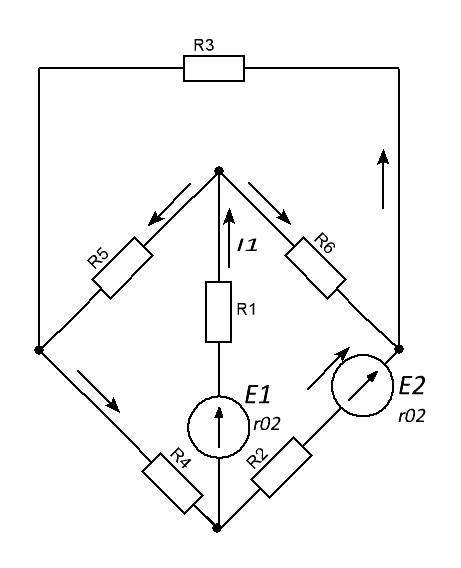
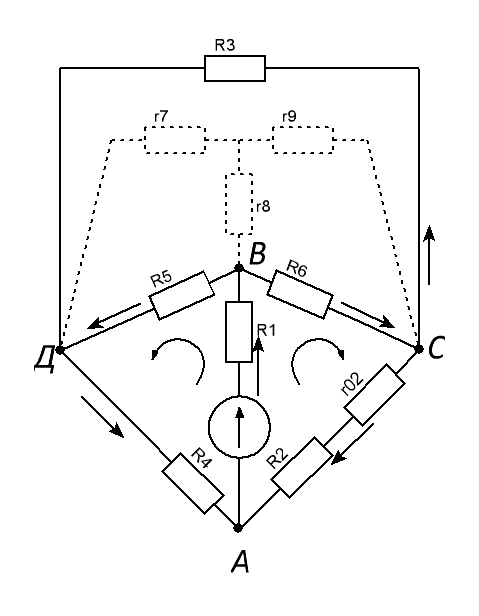
Показываем направление частных токов от ЭДС E₁ при отсутствии ЭДС Е₂, и обозначаем буквой 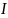c одним штрихом.

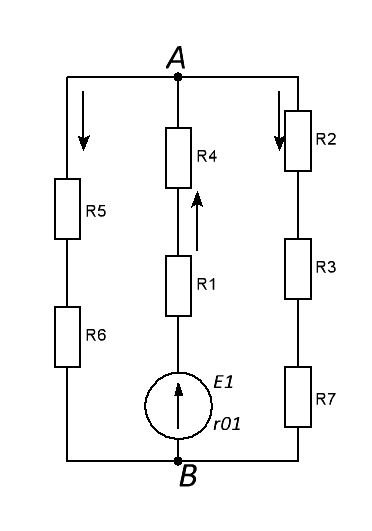
Преобразуем треугольник сопротивлений сходящихся в одной точке (имеющих один общий узел), т.е. соединенных звездой.

Для того чтобы треугольник и звезда были равнозначными (эквивалентными) друг другу необходимо выполнение следующих соотношений т.е. рассчитать сопротивления:

R_2r02 = R₂ + r₀₂ = 48+ 2= 50

R_A

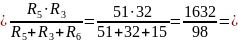
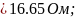
R_B

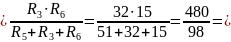
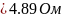
R_C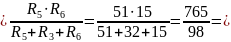

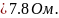
R_4A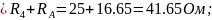

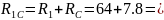
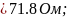
R_2,r02,B = R_2r02 + R_B = 50 + 4.89= 54.89 Oм;

R_4,2,r02,B,C= =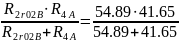

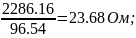
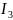
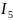
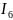
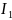
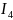
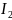
R_A

R_B

R_C

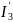
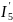
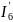
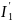
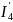
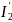
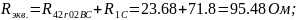
R_C

R_A

ВГПК 390202. К13. 021 ПЗ

11

Вычисляем токи источника:

;

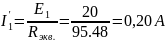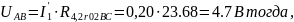
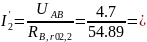0,08 A

=

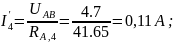
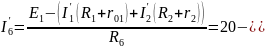
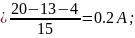
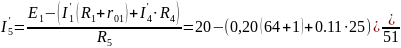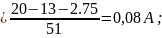
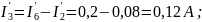
Определим частные токи от ЭДС E₂ при отсутствии ЭДС Е_1.

Показываем направление частных токов от ЭДС E₂ при отсутствии ЭДС Е₁ ,

и обозначаем буквой c двумя штрихами.

Преобразуем треугольник сопротивлений в эквивалентную звезду.

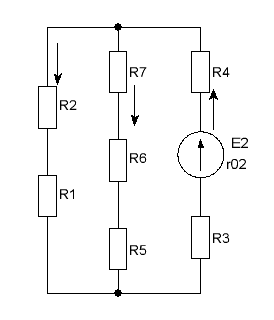
₅

R_A

R_B

R_C

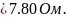
R_4A

R_A

R_B

R_C

I₃

I₆

I₅

I₁

I₄

I₂

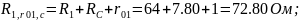
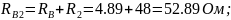
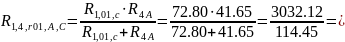
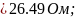
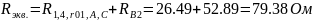
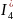
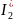
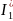
ВГПК 2390202. К13. 021 ПЗ

12

Вычисляем токи источника:

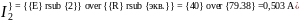
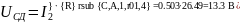
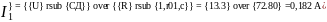
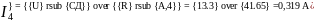
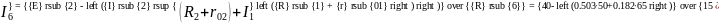
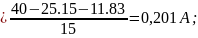
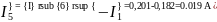
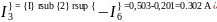
Вычисляем токи ветвей исходной цепи, выполняя алгебраическое сложение частных токов, учитывая их направление:

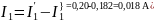
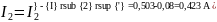
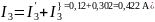
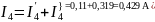
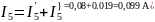
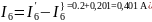
4)Составим баланс мощностей для заданной схемы.

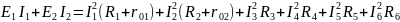
Подставляем числовые значения и вычисляем

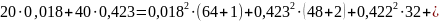
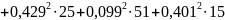
17.28 Вт=22,76 Вт

С учетом погрешностей расчетов баланс мощностей получился.

ВГПК 390202. К13. 021 ПЗ

13

5)Результаты расчетов токов по пунктам 2 и 3 представим в виде таблицы и сравним.

Токи в ветвях Метод расчета
Метод контурных токов Метод наложения	-0,028 0,018	0,430 0,423	0,285 0,422	0,402 0,429	0,117 0,099	0,145 0,401

7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

Возьмем контур АВСА. Зададимся обходом контура против часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А.

Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу.

Начнем обход от точки А.

Потен­циал этой точки равен нулю φ_А = 0

Ф_А= 0

Ф_B^,=ф_А –I₂R₂=0-20,304=-20,304 B

Ф_c=ф_B^,-I₂r₀₂+E₂=-20,304-0,846+40=18,85B

Ф_B=Ф_c-I₆R₆=18,85-6,015=12,845 B

Ф_K=Ф_B-I₁R₁-E₁ =12,845-1,152-20=-8,307B

ф_А=ф_К-I₁r₀₁=-8,307-0,018=0 – проверочная точка.

ВГПК 390202. К13. 021 ПЗ

14