РГУ нефти и газа им. И.М. Губкина

(Оренбургский филиал)

ЛАБОРАТОРНАЯ РАБОТА № 342

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА ПО

СПЕКТРУ АТОМАРНОГО ВОДОРОДА

Г. ОРЕНБУРГ.

2011г.

. ЦЕЛЬ И СОДЕРЖАНИЕ РАБОТЫ

Целью работы: ознакомление с закономерностями в спектре водорода. Работа состоит в градуировке спектроскопа, определении длин волн четырех спектральных линий серии Бальмера и расчете постоянной Ридберга.

. КРАТКАЯ ТЕОРИЯ РАБОТЫ

Спектры излучения изолированных атомов, например атомов разреженного одноатомного газа или паров металла, состоят из отдельных спектральных линий и носят название линейчатых. Относительная простота линейчатых спектров объясняется тем, что электроны, входящие в состав таких атомов, находятся под действием только внутриатомных сил и практически не испытывают возмущающего действия со стороны окружающих удаленных атомов. Изучение линейчатых спектров показывает, что в расположении спектральных линий, образующих спектр, наблюдаются определенные закономерности: линии располагаются не беспорядочно, а группируются сериями. Впервые это было обнаружено для водорода Бальмером в 1885 г. Сериальные закономерности в атомных спектрах свойственны не только атому водорода, но и другим атомам и представляют собой проявление квантовых свойств излучающих атомных систем.

Частоты всех линий спектра водородного атома можно представить формулой

(1)

здесь  - частота данной линии, связанная с длинной волны

соотношением .

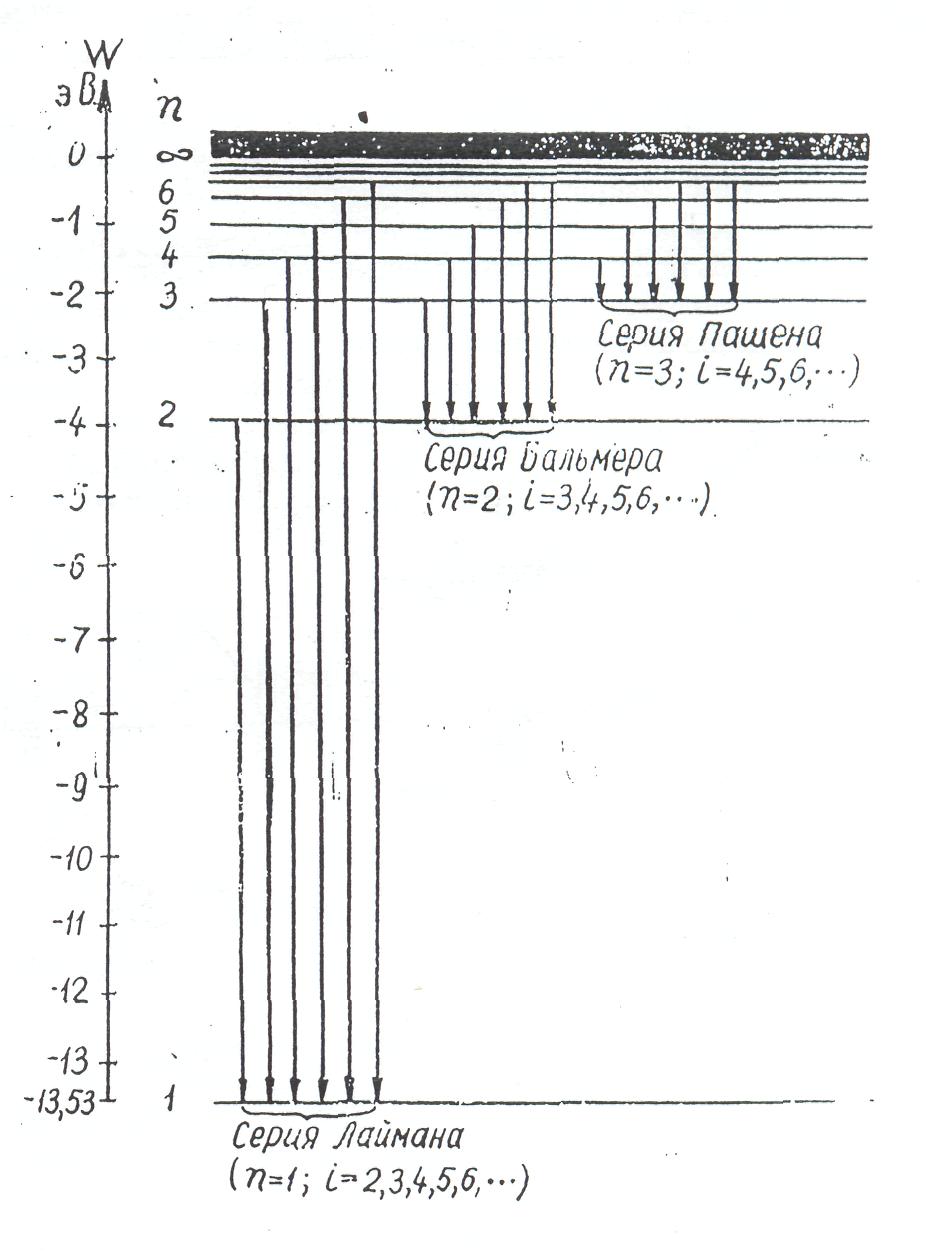
Рис. 1. Схема образования спектральных серий атомарного водорода

R– постоянная Ридберга, i – целые числа, причем in.

Формула (1) носит название обобщенной формулы Бальмера.

Наряду с частотой в спектроскопии принято характеризовать спектральные линии величиной, обратной длине волны, которая носит название волнового числа ¹:

k =  = 1/ = /с. (2)

Для волнового числа формула (1) примет вид

k = R ( 1/n² – 1/i²). (3)

Формула (3) является обобщением зависимостей, полученных на опыте для отдельных серий спектральных линий, например для серии Бальмера в видимой части спектра

k = R (1/2² – 1/i²) i = 3,4,5…,

серии Лаймана в ультрафиолетовой области

k = R (1/1² – 1/i²) n =1, i = 3,4,5…,

серии Пашена в инфракрасной области

k = R (1/3² – 1/i²) i = 4,5,6…

и т. д.

Таким образом в обобщенной формуле (3) целое число n дает номер серии, а целое число I номер той или иной спектральной линии в данной серии.

Спектральные закономерности в спектре водорода легко объясняются теорией Бора. На рис.1 схематически показано образование серии спектральных линий. Горизонтальными линиями на рисунке обозначены уровни энергии атома водорода. Стрелками указаны переходы электронов. Согласно теории Бора при переходе электронов с одного энергетического уровня на другой испускается квант энергии с волновым числом:

(4)

Сравнивая формулы (3) и (4), получим:

. (5)

В этой формуле все величины выражены в системе СИ. Постоянную Ридберга можно найти с помощью формулы (3), определив экспериментальным путем длины волн в какой-либо серии. Наиболее удобно это сделать в видимой области спектра, т. е. для серии Бальмера. В настоящей работе определяются длины волн первых четырех наиболее ярких спектральных линий серии Бальмера. В этой серии n=2, а i принимает значения: i=3 (красная линия), i=4 (голубая линия), i=5 (фиолетовая линия), i=6 (темнофиолетовая линия, слаборазличимая).

Таким образом, постоянная Ридберга определяется из четырех независимых измерений. Как будет видно из опыта, значение R при этом получится одинаковым (в пределах точности измерений). Это и означает, что линии серии Бальмера подчиняются сериальной закономерности

. (6)

III. Приборы и принадлежности, необходимые для выполнения работы

Установка, используемая в работе, состоит из монохроматора УМ-2 и двух спектральных ламп – ртутной и водородной, питание которой осуществляется от специальных устройств. Монохроматор используется в данном случае как спектроскоп, так как выходная щель монохроматора заменена окуляром, что позволяет наблюдать спектр визуально. Монохроматор служит в работе для определения длин волн линий в спектре водорода. Оптическая схема монохроматора показана на рис. 2:1 – источник света, 2 – защитное стекло щели, 3 – щель коллиматора, 4 – объектив коллиматора, 5 – диспергирующая призма, 6 – объектив зрительной трубы, 7 – указатель в фокальной плоскости окуляра, 8 – окуляр зрительной трубы.

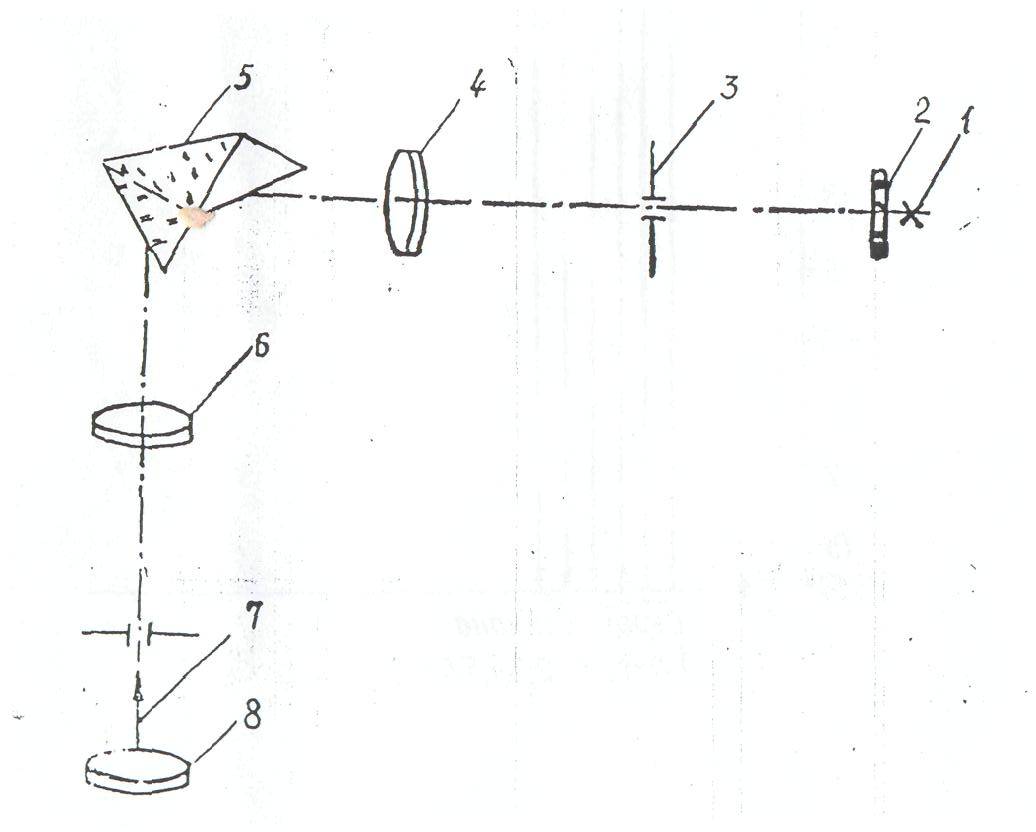
Рис. 2 – Оптическая схема монохроматора

Объектив коллиматора, в фокусе которого находится щель, образует параллельный пучок света и направляет его на призму 5. Призма преобразует этот пучок в систему параллельных пучков, выходящих из диспергирующего элемента под различными углами, зависящими от длины волны. Объектив зрительной трубы фокусирует отдельные параллельные пучки и образует в фокальной плоскости совокупность монохроматических изображений входной щели, которые и представляют собой спектры, наблюдаемые с помощью окуляра.

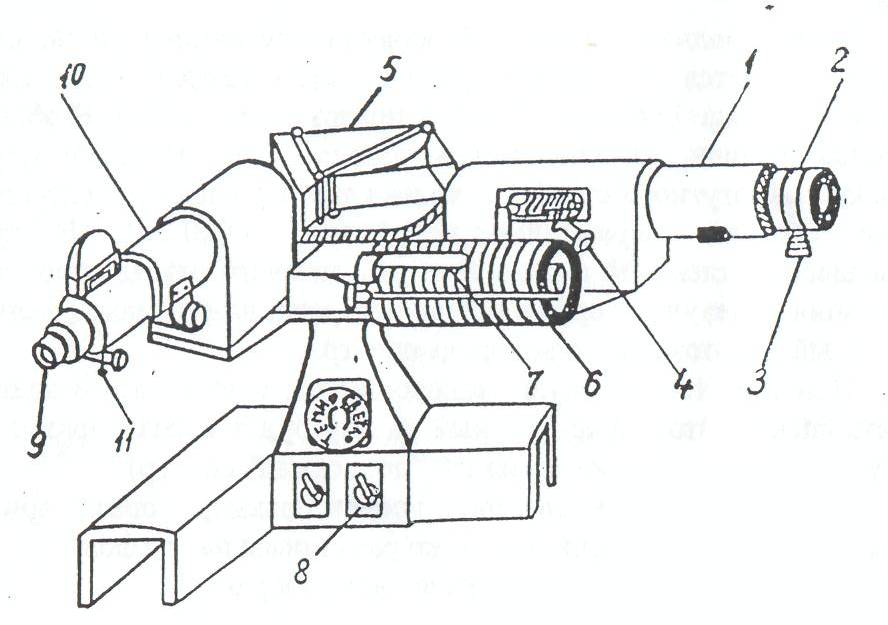
Рис. 3. Общий вид монохроматора

Общий вид монохроматора показан на рис. 3: 1 – коллиматор, 2 – щель, величина которой регулируется микрометрическим винтом 3. Винт 4 служит для фокусировки изображения спектральных линий. Поворот призмы 5 осуществляется вращением барабана 6. В зависимости от положения призмы в поле зрения попадает тот или иной участок спектра. На барабане нанесена шкала в относительных делениях – градусах поворота самого барабана. Шкала барабана освещается осветителем 7, включение которого производится тумблером 8. В фокальной плоскости окуляра 9 зрительной трубы 10 находится указатель 11 (см. рис. 2 указатель 7).