6.4. Моделирование инфляции

6.4.1. Постановка задачи. Основные уравнения. Инфляция - обесценивание денег, когда на ту же самую сумму некоторое время спустя можно купить меньший объем товара. Она возникает при нарушении баланса между товарным и денежным потоками. Внешний признак инфляции - непрерывный рост цен в течение достаточно длительного времени.

Глубинным источником инфляции является разлад взаимодействия производственной и финансово - кредитной подсистем экономики. Удачное государственное вмешательство может смягчить инфляцию, неудачное - усугубить ее.

Рассмотрим моделирование инфляции на модели стационарных сбалансированных состояний трехсекторной экономики. Предположим, что распределение инвестиций является постоянным, налоги в явном виде не рассматриваются.

Стационарное состояние трехсекторной экономики при сделанных предположения задается девятью параметрами , - доли векторов в распределении труда, , - цены и , - годовые ставки заработной платы и балансами в относительных показателях.

Баланс распределения труда между секторами

. (6.39)

Материальный баланс

. (6.40)

Баланс доходов и расходов материального сектора

. (6.41)

Баланс доходов и расходов фондосоздающего сектора

. (6.42)

Баланс спроса и предложения

, (6.43)

Выражения для стационарных удельных выпусков секторов , , если абсолютные выпуски заданы функциями Кобба - Дугласа, аналогично (6.7) имеют следующий вид

, , (6.44)

, , .

, - коэффициенты нейтрального технического прогресса и эластичностей по фондам секторов, , - коэффициенты износа по секторам, -темп прироста числа занятых.

Дифференцируя условия сбалансированности (6.39)-(6.43), получаем следующие уравнения для малых изменений долей труда и цен .

,

,

, (6.45)

,

,

где дифференциалы производительностей секторов определяются по их выражениям, представленным в (6.44):

(6.46)

Подставив соотношения (6.46) во второе уравнение (6.45) и разделив обе его части на , получим вместе с первым уравнением следующую систему для

(6.47)

где .

Уравнения (6.47) имеют решение относительно , :

(6.48)

где , , .

Подставив (6.46) и (6.44) в третье, четвертое и пятое уравнения системы (6.45), получим систему основных уравнений для анализа инфляции

Замечание. Ниже в исследовании важное значение имеет поведение (знаки) следующих выражений (их можно назвать индикаторами трехсекторной экономики):

, , - доли фондосоздающего и потребительского секторов в расходе продукции материального сектора (при выполнении материального баланса );

(при и , растет с ростом при выполнении трудового и материального балансов);

(6.50)

Доказательство этих свойств можно найти в [5].

6.4.2. Виток инфляции. Первый полувиток инфляции. Рассмотрим один виток инфляции: повышение ставки заработной платы в потребительском секторе приводит к повышению цены на предметы потребления и тем самым к падению реальной ЗП в материальном и фондосоздающем секторах. Для сохранения реальной ЗП приходится повышать цены за свою продукцию, а это приводит к повышению цены на продукцию потребительского сектора, следовательно, реальная ЗП в нем падает (номинальная постоянна). Для сохранения реальной ЗП в потребительском секторе надо вновь поднимать цены на его продукцию, что означает начало нового витка инфляции.

Исследование одного витка инфляции имеет на два этапа:

1) повышение ставки ЗП в потребительском секторе и реакция на это материального и фондосоздающего секторов (первый полувиток инфляции)

2) повышение ставок ЗП в материальном и фондосоздающем секторах с целью сохранения реальной ЗП и отражение этой акции на цене продукции потребительского сектора (второй полувиток инфляции).

Как видно из описания полувитков, инфляция не обязательно может начаться в потребительском секторе. Инициаторами ее могут быть и материальный и фондосоздающий секторы.

Пусть ставка ЗП в потребительском секторе возросла от значения до значения , >0, материальный и фондосоздающий секторы еще не успели среагировать на это увеличение, т.е. =0 , =0 . Увеличение оплаты труда в потребительском секторе приводит к переливу труда в этот сектор, т.е. . В этом случае система (6.45) имеет вид

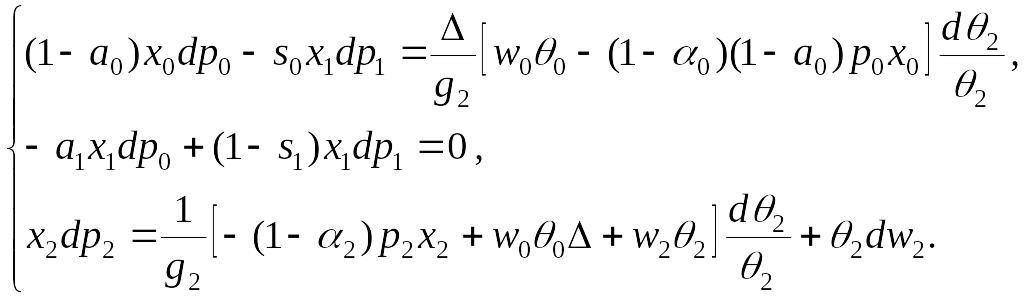(6.51)

Решение этой системы будет иметь вид

,

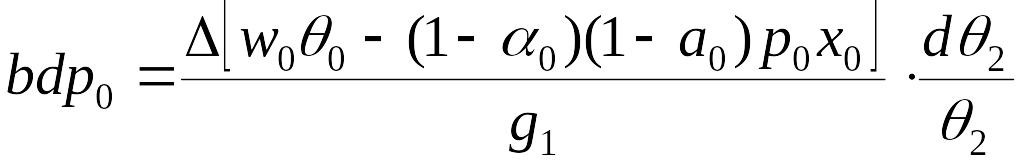, (6.52)

.

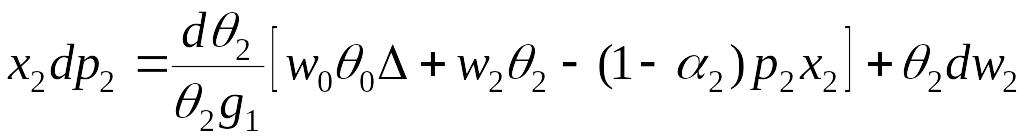Так как и согласно замечанию 6.5.1 , то знак и , определяется выражение , поэтому и , при

(6.53)

Исследуем изменение цены продукции потребительского сектора, используя 3-е уравнение (6.52).

Так как , то для того, чтобы выполнялось неравенство , достаточно выполнения условия

(6.54)

Таким образом, при росте ставки ЗП в потребительском секторе цена на его продукцию при выполнении условия (6.50) возрастает, тем самым при постоянстве номинальной заработной платы в материальном и фондосоздающем секторах реальная ЗП упадет от значений , до значений , .