1. Графтар теориясының негізгі ұғымдары мен анықтамалары (н-граф және орграф, мультиграф, инциденттік, сыбайластық, төбелер дәрежесі).

Кейбір қолданбалы математика есептерінде бірнеше объектілер арасындағы байланыс жүйелері зерттеледі. Объектілер төбелер деп аталып, олар нүктемен белгіленеді, ал осы төбелер арасындағы байланыс доғалар д. а.сәйкес нүктелер арасына стрелкалар бел/з, осындай жүйелер графты

құр-ды.

Графта объектілер арасындағы байланысты сипаттайтын белгілі, ал байланыс бағытталған немесе бағытталмаған болуы мүмкін. Сондықтан графтар теориясында графтың негізгі екі түрін қарастырады: орграф – бағытталған г., н-граф – бағытталмаған..

Н-граф1. {u,v} қабырғасы u және v төбелеріне инциденттелген, керісінше u және v төбелері {u,v} қабырғаларына инциденттелген д.а.

u және v нүктелері қабырғаның шеткі нүктелері болса, онда u және v төбелері сыбайлас д.а.

v төбесінің дәрежеі деп оған инцидентті қабырғалар санын айт/з – ρ(v)

Орграф u және v төбелеріне (u,v) доғасына инцидентті д.а. Егер доға v төбесінен басталса н/е v төбесіне батса, онда ол доға v төбесіне инцидентті д.а.Доғаның u басы vсоңы болатын төбелер сыбайлас д.а.

v төбесінің шығу дәрежесі деп v төбесінде басы болатын доғалар саны – ρ₁(v)

кіру дәрежесі деп v төбесі соңы болатын доғалар санын айтамыз – ρ₂(v)

2.Графтың берілу жолдары (G=(V,E) жиындар жұбы, сурет, инциденттік матрицасы, қабырғалар(доғалар) тізімі).

1) Графты V және E (төбелер, қабырғалар) жиындарының жұбы арқылы беруге болады: G=G(V,E). Қабырғалар жиыны арқылы да беруге болады, онда әрбір қабырға шеткі төбелерінің жұбын білдіреді. V={a,b,c}, E={e1,e2},

E={{a,b},{b,c}} – н-граф, E={(a,b),(b,c)} – орграф.

3)G графының инциденттік матрицасы деп өлшемі m*n болатын (a_ij) матрицасын айтамыз, оның элементтері келесі жолмен анықталады.

н-граф

орграф:

4) Бұл тізім 2 бағаннан тұрады: 1-қабылар, 2-осы қабырғаға инцидентті төбелер. Нграф үшін төбелер реті қалауынша жазылады, орграф үшін алдымен доғаның басының нөмері жазылады.

2.Графтар мен бинарлы қатынастар арасындағы байланыс. Графтардың изоморфизмі. Ішкі графтар. Графтарға қолданылатын қисаптар.

Графтар мен бинарлы қатынастар.

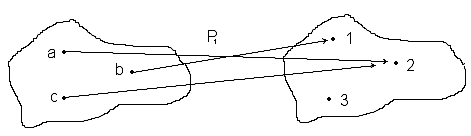
Бинарлық қатынастарды графиктік түрде Граф арқылы да кескіндеуге болады. Мысалы, P₂={(a,b),(b,b),(c,a)} қат/ның граф түріндегі бейнесі 6-суреттегідей болады.

V жиынында берілген R қатынасына өзара бір мәнді анықталған, орындалса ғана қабырғасы бар болатын V төбелер жиындарымен қабырғалар еселі емес бағытталған G(R) графы сәйкес келеді.

1-мысал: Симметриялы, антисиметриялы, рефлексивті, антирефлексивті, транзитивті R бинарлы қатынасына өзара бір мәнді сәйкес G графының қандай ерекшеліктері бар?

Айталық , R бинарлы қатынасы жиынында анықталсын.

а) симметриялы R қатынасына еселі қабырғалары жоқ, орындалса ғана қабырғасы бар болатын бағытталмаған G(R) графы сәйкес келеді (симметриялы болғандықтан ).

б) Антисиметриялы R қатынасына еселі қабырғаларсыз,(әртүрлі төбелерге қарама-қарсы бағытталған қабырғалары бар төбелер болмайтын) өзара бір мәнді бағытталған G(R) графы сәйкес келеді .

в) Егер R рефлексивті болса, барлық төбелерінде ілгектері бар еселі қабырғаларсыз G(R) графы сәйкес келеді.

г) Егер R антирефлексивті болса, еселі қабырғаларсыз G(R) графында бір де бір ілгек болмайды.

д) Егер R транзитивті болса, еселі қабырғаларсыз G(R) графының әрбір және қабырғалар жұбына оларды тұйықтайтын қабырғасы бар болады.

Тек қана төбелерінің және қабырғаларының нөмірленуінде ғана айырм/ғы бар графтар изоморфты графтар деп аталады. Егер e1=(u,v)ϵE1  e2=(φ(u),φ(v))ϵE2 сыбайластықты сақтайтын биекция φ:V1->V2 бар болса, онда G1=(V1,E1) және G2=(V2,E2) графтары изоморфтыдеп аталып, G1~G2 деп белгіленеді.

Графтың изоморфизмі эквива/к қат/с болып таб/ы. Расында изоморфизм эквиваленттік қатынастың барлық қасиетіне сай келеді: а) рефлексивті (G~G); ә)симметриялы (G1~G2= > G2~G1); б)транзитивті (G1~G2, G2~G3= > G1~G3)

Графтарды изоморфизм дәлдігіне дейін қарастыруға болады. Барлық изоморфты графтар үшін бірдей сандық характеристикалар графтың инварианты деп аталады.

Граф бөліктеріне қолданылатын амалдар.

Граф бөліктеріне төмендегідей амалдар орындалады:

Н-бөліктің толықтаушы -G-графының Н-ға жатпайтын барлық қаб/р жиынымен анықт/ды. , мұндағы E(G)-G-графының қаб/ң жиыны.

- G графының Н₁, Н₂ бөліктерінің қосындысы :

- және ;

- G графының Н₁, Н₂ бөліктерінің көбейтіндісі : және ;

Егер H₁, H₂ бөліктерінің ортақ төбелері болмаса, яғни , демек ортақ қабырғалары да жоқ , онда H₁, H₂ бөліктері төбелері бойынша қиылыспайды.

Егер H₁, H₂ бөліктерінің ортақ қабырғалары болмаса ,онда H₁ , H₂ бөліктері қабырғалары бойынша қиылыспайды.

Егер болса онда тура қосынды деп аталады.

G=<M,R>,G¹=<M¹,R¹> графтары берілсін. Егер М¹ М және R¹=R∩(M¹)² болса, яғни G¹ графының төбелер жиыны G-ң төбелер жиынында жатса ал G¹-ң доғалары екі жағымен де G графына жатса G¹–G графының ішкі графы деп аталады.

4.Маршруттар, шынжыр, жолдар, циклдар, контурлар. Байланыстылық , мықты байланыстылық, байланыстылық компоненталары.Граф жолдары (маршруты)деп - Еі-1 және Еі көршілес қабырғалары бір төбеде қиылысатындай, оның әртүрлі(Е0, Е1,..., Ек ) қабырғаларының шекті тізбегін айтады .Сонымен , егер, (Е0, Е1,..., Ек )- жол болса, онда Е0= (а0,а1) Е1= (а1,а2),.... Еm =(аm, аm+1)олар жолдың ішкі төбелері деп аталады.Барлық төбелері ішкі болатын жол –тұйықталған жол деп аталады. Барлық қабырғалары әртүрлі болатын жолды шынжыр деп атаймыз. Тұйықталған шынжыр – цикл деп аталады. Егер шынжырдың немесе циклдің барлық төбесі бір рет кездесетін болса, онда шынжыр немесе цикл– жай деп аталады.Егер кез келген екі беттеспейтін төбелері маршрутпен қосылса, онда G н-графы байланысқан де аталады.

Егер G орграфына сәйкес н-граф байланысқан болса, онда G орграфы да байланысқан деп аталады. Егер кез келген u және v екі төбесі өзара қолжетерлік болса, яғни, u төбесі v төбесінен, ал v төбесі u төбесінен жетерлік болса, онда орграф мықты байланысқан деп аталады.

Келесі шарттар орындалсын:

А) G1 – бос емес байланысқан (мықты байланысқан) граф;

Ә) егер G2-G1 графының байланысқан (мықты байланысқан) ішкі графы және G1≤G2болса, онда G1=G2яғни G1−G графының максималды байланысқан (мықты байланысқан) ішкі графы болады.

Егер осы екі шарт орындалса, онда G графының G1 ішкі графы G(V,E) графының байланыстық компонентасы (байланыстықтың мықты компонентасы) де аталады.

5.Байланыстылық және мықты байланыстылық компонеталарының анықтамасы. Жетерлік матрица.

Егер кез келген екі беттеспейтін төбелер маршрутпен қосылса, онда G н-графы байланысқан д.а.

Егер кез келген u және v екі төбесі өзара қолжетерлік б.о. орграф мықты байланысқан д.а.

Егер c_ij={1, егер j төбе i төбеден қолжетерлік болса

0, қарсы жағдайда

Элементтерінен тұратын m x n өлшемді (m=[v]төбелер саны)шаршы C=c_ij матр қолжетерлік д.а.(н граф үшін сыбайлас матр).

Анықтау жолдары: Орграф үшін қолжетерлік матрица көмегімен графтың мықты компе/рын табуга болады. C=c_ij матр басқа Q=c^T=(g_ij)матр қараст.

g_ij={1, егер j төбе I төбеден қолжетерлік болса

0, қарсы жағдайда

S=(s_ij)=C*Q S_ij= c_ij*q_ij

_Vi ж/е _Vj төбелері өзара қолжетерлік б.о. олар графтың бір мыkты байл компен-да орна/ды ж/е S матр сәйкес элементі 1ге тең S_ij=1

Н-граф үшін сыбайлас матр колжетерлік матр болады. S_ij=1б.о байл. Жалпы н- графтың S_ij матр графтың төбелер жиынын компе.ге бөліктеуіне сәйкес келетін эквиваленттік қатынастын матр б.т.