3.3. Поиск технических решений с помощью эвм

Процедура поиска ТР заключается в составлении функционального и структурного описания ПО и определяется как установление бинарных отношений между множеством признаков P и множеством технических решений G.

Метод выполнения процедуры выбирается в зависимости от того, на что направлено проектирование - на улучшение существующей конструкции или на создание новой. Для автоматизированного поиска средств улучшения конструкции наиболее целесообразен метод И-ИЛИ-дерева, представляющий удачный симбиоз морфологического и системного подходов.

Описание структуры ТС должно включать информацию о функциональных элементах (ФЭ), их взаимном расположении и взаимосвязи. Для описания множества связей между ФЭ требуется база данных, логическая организация которой может быть построена по аналогии с классификацией механизмов в справочнике И.И.Артоболевского. Представляя ФЭ в виде вершин, а связи между ними в виде ребер, строят граф G = T{E, U}, где E = {e} - множество вершин; U - множество ребер (связей).

При построении дерева технических решений выполняют операции разбиения ФЭ более высокого иерархического уровня на ФЭ более низкого уровня:

1) изучают проектируемую ТС и определяют ее общую функцию;

2) разбивают ТС на подсистемы так, чтобы выполняемые ими функции полностью обеспечивали выполнение общей функции;

3) далее на последующих уровнях выделяют ФЭ по их частным функциям.

Требования системного подхода определяют число уровней в графе не менее пяти. Это тот уровень, который соответствует принципу делимости систем. Следует отметить, что наглядность рисунка графа исчезает по мере увеличения числа ФЭ (практически при более сорока). Если связи указывают лишь соподчиненность ФЭ, находящихся на разных иерархических уровнях (система-подсистема-комплект-узел-детали), и все ФЭ представляют непересекающиеся множества входящих в них компонентов, то граф приобретает форму дерева.

ФЭ различного функционального назначения обозначаются на графе вершинами типа И, а одинакового (но отличающиеся исполнением, т.е. альтернативные) - вершинами типа ИЛИ. Древовидный граф с вершинами И и ИЛИ получил название И-ИЛИ-дерева, которое в компактном виде хранит информацию о множестве всех ТР, относящихся как к машине в целом, так и к ее ФЭ.

Построение И-ИЛИ-дерева представляет трудоемкий процесс, при реализации которого можно использовать различные подходы:

1) дерево строится вначале по одному ТР, а затем достраивается по другим ТР;

2) деревья строятся по всем ТР, а затем объединяются;

3) множество ТР разбивается на подмножества, внутри каждого из них строится дерево, а затем они объединяются.

Для ввода построенного дерева в ЭВМ его необходимо представить в виде матрицы смежностей (матрицы инциденций), которая представляет собой треугольную матрицу nn, где n - число вершин дерева. По строкам располагаются вершины, из которых выходит ребро (т.е. вершины-предшественники), а по столбцам - вершины, в которые ребро входит (вершины-последователи). На пересечении вершин, соединенных ребром, ставится единица, а несоединенных - нуль (который обычно не проставляется). Для кодирования типа вершины предусматривается дополнительный столбец за пределами матрицы, определенный на множестве {0, 1, 2}, где 1 соответствует вершине типа “И”, 2 - типа “ИЛИ”, а 0 - “висячей” вершине (не имеющей связи с нижележащими вершинами).

Однако И-ИЛИ-дерево несет информацию только о структуре и конструктивных элементах проектируемой ТС, что недостаточно для выбора вариантов. Поэтому дерево необходимо дополнить средством формального отражения на множестве технических решений функций и признаков. Для этого можно воспользоваться матрицей соответствий, строками которой являются ФЭ, а столбцами - признаки. Матрица определена на множестве значений {–1, 0, +1}. Если ФЭ способствует достижению признака (т.е. увеличивает его значение), то на пересечении соответствующей строки и столбца ставится (+1), если не способствует (т.е. уменьшает) - то (–1), а если не влияет (т.е. обеспечивает среднее значение или вообще не связан с данным признаком) - то (0). Для учета важности различных показателей нужно также концептуальное описание. Таким образом, необходимыми данными для поиска вариантов ТР с помощью ЭВМ являются:

- дерево технических решений (И-ИЛИ-дерево);

- матрица соответствий;

- концептуальное описание.

Рассмотрим работу алгоритма выбора вариантов ТС на примере дерева, представленного на рис. 3.1. Дерево построено для вакуумного модуля весьма укрупненно, где в качестве корневой вершины (е₀) выступает вакуумный модуль, а среди основных функциональных систем выделена только вакуумная система (е₁). Другими ФЭ являются вакуумные насосы (е₂) и элементы коммутации (е₃). Среди вакуумных насосов выбор проводится на множестве форвакуумных (е₄) и высоковакуумных (е₅) насосов. В качестве элементов коммутации выделены клапаны (е₆) и затворы (е₇), выбор форвакуумных насосов проводится среди пластинчато-роторных (е₈), пластинчато-статорных (е₉) и плунжерных (е₁₀), а высоковакуумных - среди струйных (диффузионных паромасляных - е₁₁), турбомолекулярных (е₁₂) и криогенных (е₁₃) вакуумных насосов.

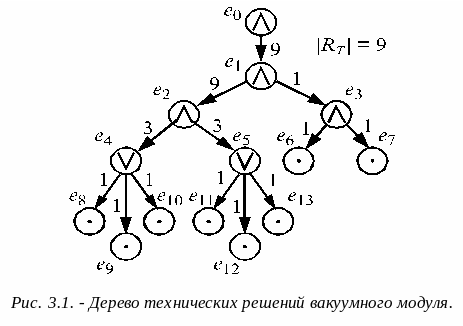
Матрица смежностей дерева приведена в табл. 3.2, а матрица соответствий - в табл. 3.3. В качестве признаков выбраны: производительность (Р₁), степень чистоты среды в модуле (Р₂), предельный вакуум (Р₃), минимальное время запуска (Р₄), максимальное давление запуска (Р₅), низкий уровень вибраций и шума (Р₆), длительность непрерывной работы (Р₇), габариты (Р₈), проводимость (Р₉) и быстродействие (Р₁₀).

Алгоритм выбора вариантов ТС состоит из двух частей:

1. определение теоретического множества вариантов;

2. нахождение рациональных вариантов.

Таблица 3.2. - Матрица смежностей И-ИЛИ-дерева, представленного на рис.3.1.

е1	е2	е3	е4	е5	е6	е7	е8	е9	е10	е11	е12	е13	Е	Код
0	1	1	0	0	0	0	0	0	0	0	0	0	е1	1
	0	0	1	1	0	0	0	0	0	0	0	0	е2	1
		0	0	0	1	1	0	0	0	0	0	0	е3	1
			0	0	0	0	1	1	1	0	0	0	е4	2
				0	0	0	0	0	0	1	1	1	е5	2
					0	0	0	0	0	0	0	0	е6	0
						0	0	0	0	0	0	0	е7	0
							0	0	0	0	0	0	е8	0
								0	0	0	0	0	е9	0
									0	0	0	0	е10	0
										0	0	0	е11	0
											0	0	е12	0
												0	е13	0

Таблица 3.3. - Матрица соответствий И-ИЛИ-дерева, приведенного на рис.3.1.

еi	Р1	Р2	Р3	Р4	Р5	Р6	Р7	Р8	Р9	Р10
е4	-1	-1	-1	1	1	-1	1	0	0	0
е5	1	0	1	-1	-1	1	0	0	0	0
е6	0	0	0	0	0	0	0	1	-1	1
е7	0	0	0	0	0	0	0	-1	1	-1
е8	0	-1	-1	1	1	-1	1	1	0	0
е9	-1	-1	-1	1	1	-1	1	1	0	0
е10	1	-1	-1	1	1	-1	1	-1	0	0
е11	1	-1	1	-1	-1	1	1	-1	0	0
е12	1	1	1	-1	0	0	1	-1	0	0
е13	1	1	1	-1	1	0	-1	0	0	0

Определение теоретического множества вариантов ТР осуществляется по следующему алгоритму:

1) помечаются все “висячие” вершины (на графе вершины “И” отмечаются знаком конъюнкции (Λ), вершины “ИЛИ” - знаком дизъюнкции (V), а “висячие” - точкой (•)); ребрам, заходящим в них, присваивается вес, равный 1;

2) находится непомеченная вершина, такая, что все исходящие из нее ребра имеют некоторые веса;

3) если найденная вершина относится к типу “И”, то ребру, входящему в нее, присваивается вес, равный произведению весов исходящих из нее дуг, а если “ИЛИ” - то сумме;

4) движение по вершинам дерева осуществляется от “висячих” к корневой; мощность теоретического множества решений |R_T| равна произведению исходящих из корневой вершины дуг, если она типа “И”, и сумме, если типа “ИЛИ”.

Для примера, приведенного на рис.3.1, получаем |R_T| = 9, т.е. возможны девять комбинаций ФЭ при поиске ТР. Для того, чтобы определить, сколько вариантов из этих девяти являются рациональными, т.е. удовлетворяющими требованиям ТЗ, можно использовать следующий алгоритм:

1) двигаемся по дереву сверху вниз от корневой вершины, включив ее в описание ТР, строго по возрастанию номера вершины, анализируя тип вершины-предшественника (т.е. выбираем столбец матрицы смежностей, соответствующий рассматриваемой вершине e_i, и определяем строку, на пересечении с которой стоит 1; эта строка и будет соответствовать вершине-предшественнику);

2) если предшественником e_i является вершина типа “И”, то e_i включаем в описание ТР, а если “ИЛИ”, то находим все вершины-последователи этого предшественника (помимо e_i ими будут все вершины по столбцам, которые имеют 1 в строке, соответствующей вершине-предшественнику);

3) рассматриваем все ТР по вершинам-последователям и выбираем то из них, которое в большей степени отвечает признакам и концептуальному описанию (используем матрицу соответствий и КО); при этом возможны следующие пять случаев:

а) если вершина e_i является единственным последователем своего предшественника, то она включается в описание ТР;

б) если среди рассматриваемой группы вершин-последователей имеется одна, отвечающая всем признакам КО (т.е. в соответствующей ей строке матрицы соответствий стоят 1), то она включается в описание ТР, а все остальные вершины из группы исключаются из последующего рассмотрения;

в) если вершины рассматриваемой группы в разной степени удовлетворяют или не удовлетворяют признакам КО, то выбирается та из них, которая отвечает большему числу признаков (имеет больше 1 в строке матрицы соответствий), а при его равенстве отдается предпочтение той вершине, которая удовлетворяет признакам, соответствующим наиболее важным целям (т.е. дополнительно обращаются к КО, в котором цели расположены в ранжированной последовательности по мере важности); остальные вершины исключаются из дальнейшего рассмотрения;

г) если из рассматриваемых вершин две и более удовлетворяют признакам КО, то произвольным образом выбирается одна из них, а другие оставляются для последующего рассмотрения (эта ситуация соответствует наличию альтернативных ТР);

д) если ни одна из рассматриваемых вершин не удовлетворяет ни одному из признаков КО, то действуют так же, как в пункте г);

4) при анализе каждой очередной по номеру вершины e_i проводим проверку на исключение ее из описания ТР; вершина исключается из рассмотрения на данном шаге, если на предыдущих шагах:

а) вершина уже включена в описание;

б) вершина уже исключена из описания;

в) предшественник ее исключен из описания;

5) цикл поиска решения заканчиваем, когда i ≥n, где n - наибольшее значение индекса вершины e_i на дереве; выводим описание полученного варианта ТР и приступаем к следующему циклу поиска ТР;

6) процедуру поиска ТР заканчиваем, если выполняется одно из следующих условий:

а) число описаний достигло множества комбинаций |R_T|;

б) число описаний достигло заданного числа комбинаций;

в) исчерпано время, отведенное на выполнение процедуры.

Конструктор может прекратить поиск ТР после нахождения нескольких рациональных вариантов и попытаться определить наилучший из них, т.е. в максимальной степени удовлетворяющий признакам КО. Оптимальным вариантом будет тот, для которого ФЭ в матрице соответствий не содержат значений (–1) для всех признаков, вошедших в КО. С целью оптимизации конструктор может продолжить поиск, добавив в дерево новые ФЭ типа “ИЛИ”, в большей степени удовлетворяющие КО. Вопросы оптимизации ТС и методы выбора оптимального варианта будут рассмотрены ниже.

После принятия варианта ТР необходимо провести его анализ. Для этой цели существуют различные методы моделирования и анализа ТС: эвристические (на основе опыта конструктора), экспериментальные (на натурных моделях), аналитические (на математических моделях), графо-аналитические (кинематические схемы, эквивалентные схемы, графы), имитационные.

Рассмотрим описанный алгоритм поиска рациональных ТР для примера, приведенного на рис.3.1 и в табл.3.2 и 3.3. Пусть КО для нашего случая имеет вид

КО = {a₀ [a₁ (P₁, P₄, P₅, P₇, P₉, P₁₀); а₂ (Р₂, Р₃); а₃ (Р₆)]}.

Согласно п.п. 1 и 2 алгоритма, в описание ТР будут включены ФЭ с е₁ по е₇, поскольку они все имеют предшественниками вершины типа “И”. Группами альтернативных ФЭ являются е₈ - е₁₀ (предшественник е₄) и е₁₁ - е₁₃ (предшественник е₅). Из матрицы соответствий следует, что из первой группы будет выбран ФЭ е₈, поскольку он имеет меньшее число (–1) при одинаковом числе (+1), т.е. удовлетворяет большему числу признаков. Правда, если не учитывать признак Р₈ (габариты системы) как не вошедший в КО, то в этом случае наилучшим будет ФЭ е₁₀.

Для второй группы альтернативными по матрице соответствий будут ФЭ е₁₂ и е₁₃, поскольку имеют одинаковое число значений (+1) и (–1). Обращение к КО показывает, что следует выбрать ФЭ е₁₂, поскольку ФЭ е₁₃ отрицательно влияет на параметр Р₇, вошедший в КО и влияющий на достижение наиболее важной цели а₁. Таким образом, получаем одно единственное рациональное ТР.

Для реализации описанных алгоритмов поиска ТР написана программа “DEREVO”, используемая на практических занятиях.

Раздел второй ОРГАНИЗАЦИЯ РАЗРАБОТКИ И ВНЕДРЕНИЯ САПР