3. Построение закона Пуассона по вариационному ряду

Если значения признака могут приобретать лишь последовательные целочисленные значения, а средняя арифметическая и дисперсия этого распределения совпадают или мало отличаются, тогда можно ожидать, что это распределение будет довольно близким к закону Пуассона.

Пусть получен эмпирический вариационный ряд признака

			…
			…

,

который считают распределенным по закону Пуассона. Для построения этого закона следует:

• вычислить 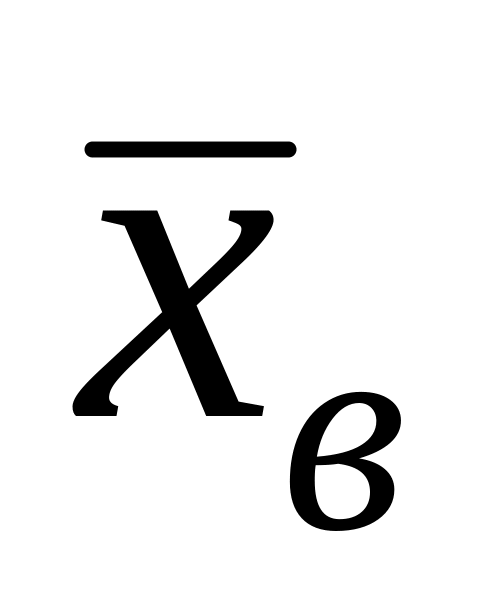и ;

• проверить их на приблизительное равенство

• взять за параметр величину .

Пример 3.

Было проведено наблюдение вызовов-заказов за время на телефонном коммутаторе:

Количество вызовов	0	1	2	3	4	5	6
Количество интервалов	235	361	231	111	42	18	2

.

Рассматриваемый признак (количество вызовов) может принимать лишь последовательные целочисленные значения. Считаем его распределенным по закону Пуассона.

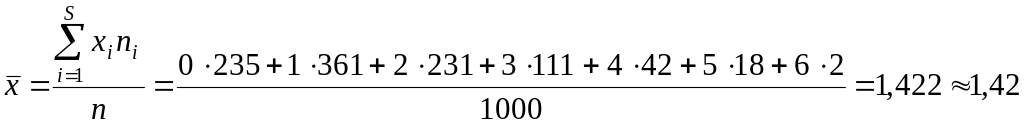
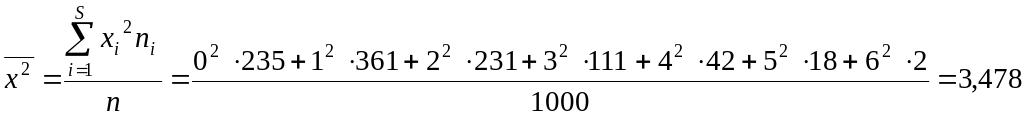
Средняя и дисперсия приблизительно равны, что дает основания сделать вывод: для этого распределения теоретическим будет закон Пуассона с параметром .

,

где

Вычисление теоретического ряда частот распределения Пуассона

Если известно, что случайная величина распределена по закону Пуассона и задано выражение этого закона, то возможным становится вычисление теоретических частот по формуле ,

Значение функции Пуассона находят по таблице

0	02417	241,7	242	235
1	0,3432	343,2	343	361
2	0,2437	243,7	244	231
3	0,1154	115,4	115	111
4	0,0409	40,9	41	42
5	0,0116	11,6	12	18
6	0,0028	2,8	3	2
	0,9993		1000	1000

3. Критерии согласия

В предшествующих примерах закон распределения считался известным или существовали довольно веские основания для предположения о форме закона распределения по данному эмпирическому материалу. Сравнение фактических и вычисленных теоретических частот указывает на их близость, но полной сходимости нет. Между и есть определенные, иногда довольно значительные расхождения. Отклонение фактических частот от теоретических можно объяснить с помощью двух утверждений:

1. Эмпирические и теоретические частоты не противоречат одна одной, а расхождения между ними необходимо считать случайными, поскольку выбор элементов исследование проводили случайным способом. Сделанное предположение о распределении признака по теоретическому закону следует признать верным.

2. Расхождения между теоретическими и эмпирическими частотами объяснить случайностью невозможно. Распределение признака по выбранному теоретическому закону необходимо признать ошибочным. Следует тщательнее изучить вариационный ряд и попробовать подобрать новый закон, который точнее учитывал бы особенности эмпирического материала.

Для выбора между этими двумя выводами применяют критерии согласия.

Критерием согласия называют правило проверки гипотезы о предположенном законе неизвестного распределения.