2. Статистическое изучение
ВЗАИМОСВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ
Важнейшей задачей любой общественной науки является выявление закономерностей изменения характеристик социально-экономических явлений. Одна из наиболее распространенных методик выявления таких зависимостей и закономерностей заключается в установлении корреляционной связи.
Корреляционная связь – это связь между факторным и результативным признаками, которая в целом проявляется в массе наблюдений, но в каждом отдельном случае более или менее сильно. Распространение характеристик корреляционной связи на каждый индивидуальный признак по-разному объясняется влиянием на этот же признак других неучтенных факторов. Поэтому корреляционная связь устанавливает среднее изменение результативного признака в зависимости от изменения признака факторного.
Рассмотрим корреляционную связь между стоимостью основных средств и груообороту, значения которых представлены в таблице 1.1.
2.1. Построение линейной модели регрессии
Регрессия – это функция, устанавливающая характер, степень и направление корреляционной зависимости результативного признака от факторного. Наиболее простой и распространенной формой регрессии является прямолинейная зависимость вида:
y(xi ) = a1xi+ a0
Для нахождения параметров уравнения регрессии в соответствии с требованиями метода наименьших квадратов строится система нормальных уравнений.
Решив систему нормальных уравнений методом Крамера, получают следующие формулы расчета параметров уравнения регрессии.
Для расчета параметров уравнения регрессии составляется таблица 2.1.
Таблица 2.1 – Расчет показателей корреляционно-регрессионной зависимости
№ предприятия |
Стоимость основных средств, млн. руб |
Грузооборот, тыс. т-км |
расчетные графы |
|||
№ |
xi |
yi |
xi*yi |
xi² |
yi² |
y(xi) |
1 |
5,9 |
124,8 |
736,32 |
34,81 |
15575,04 |
110,062 |
2 |
5,9 |
125,1 |
738,09 |
34,81 |
15650,01 |
110,062 |
3 |
7,8 |
134,7 |
1050,66 |
60,84 |
18144,09 |
129,404 |
4 |
6,7 |
138,8 |
929,96 |
44,89 |
19265,44 |
118,206 |
5 |
7,8 |
130,0 |
1014 |
60,84 |
16900 |
129,404 |
6 |
6,2 |
127,0 |
787,4 |
38,44 |
16129 |
113,116 |
7 |
6,1 |
94,3 |
575,23 |
37,21 |
8892,49 |
112,098 |
8 |
7,4 |
111,4 |
824,36 |
54,76 |
12409,96 |
125,332 |
9 |
4,3 |
94,3 |
405,49 |
18,49 |
8892,49 |
93,774 |
10 |
6,0 |
99,6 |
597,6 |
36 |
9920,16 |
111,08 |
11 |
6,2 |
127,8 |
792,36 |
38,44 |
16332,84 |
113,116 |
12 |
6,5 |
113,2 |
735,8 |
42,25 |
12814,24 |
116,17 |
13 |
7,3 |
122,2 |
892,06 |
53,29 |
14932,84 |
124,314 |
14 |
6,4 |
108,7 |
695,68 |
40,96 |
11815,69 |
115,152 |
15 |
6,6 |
105,3 |
694,98 |
43,56 |
11088,09 |
117,188 |
16 |
7,2 |
108,7 |
782,64 |
51,84 |
11815,69 |
123,296 |
17 |
7,0 |
113,9 |
797,3 |
49 |
12973,21 |
121,26 |
18 |
6,2 |
110,2 |
683,24 |
38,44 |
12144,04 |
113,116 |
19 |
6,6 |
102,1 |
673,86 |
43,56 |
10424,41 |
117,188 |
20 |
7,2 |
121,1 |
871,92 |
51,84 |
14665,21 |
123,296 |
21 |
7,3 |
112,7 |
822,71 |
53,29 |
12701,29 |
124,314 |
22 |
6,7 |
136,8 |
916,56 |
44,89 |
18714,24 |
118,206 |
23 |
7,6 |
115,5 |
877,8 |
57,76 |
13340,25 |
127,368 |
24 |
7,6 |
142,1 |
1079,96 |
57,76 |
20192,41 |
127,368 |
25 |
5,6 |
104,5 |
585,2 |
31,36 |
10920,25 |
107,008 |
26 |
7,5 |
124,5 |
933,75 |
56,25 |
15500,25 |
126,35 |
27 |
5,8 |
100,0 |
580 |
33,64 |
10000 |
109,044 |
28 |
4,7 |
100,9 |
474,23 |
22,09 |
10180,81 |
97,846 |
29 |
7,3 |
124,8 |
911,04 |
53,29 |
15575,04 |
124,314 |
30 |
6,2 |
120,1 |
744,62 |
38,44 |
14424,01 |
113,116 |
31 |
7,6 |
130,2 |
989,52 |
57,76 |
16952,04 |
127,368 |
32 |
6,3 |
98,6 |
621,18 |
39,69 |
9721,96 |
114,134 |
33 |
5,9 |
92,6 |
546,34 |
34,81 |
8574,76 |
110,062 |
34 |
5,8 |
84,1 |
487,78 |
33,64 |
7072,81 |
109,044 |
35 |
6,0 |
121,1 |
726,6 |
36 |
14665,21 |
111,08 |
36 |
7,7 |
132,2 |
1017,94 |
59,29 |
17476,84 |
128,386 |
37 |
6,8 |
127,8 |
869,04 |
46,24 |
16332,84 |
119,224 |
38 |
5,2 |
103,7 |
539,24 |
27,04 |
10753,69 |
102,936 |
39 |
5,9 |
111,9 |
660,21 |
34,81 |
12521,61 |
110,062 |
40 |
6,9 |
135,2 |
932,88 |
47,61 |
18279,04 |
120,242 |
41 |
7,2 |
139,0 |
1000,8 |
51,84 |
19321 |
123,296 |
42 |
5,7 |
117,7 |
670,89 |
32,49 |
13853,29 |
108,026 |
43 |
6,1 |
131,0 |
799,1 |
37,21 |
17161 |
112,098 |
44 |
6,7 |
125,4 |
840,18 |
44,89 |
15725,16 |
118,206 |
45 |
6,3 |
113,8 |
716,94 |
39,69 |
12950,44 |
114,134 |
46 |
6,7 |
115,2 |
771,84 |
44,89 |
13271,04 |
118,206 |
47 |
6,2 |
114,3 |
708,66 |
38,44 |
13064,49 |
113,116 |
48 |
6,3 |
102,7 |
647,01 |
39,69 |
10547,29 |
114,134 |
49 |
5,1 |
107,5 |
548,25 |
26,01 |
11556,25 |
101,918 |
50 |
5,9 |
100,2 |
591,18 |
34,81 |
10040,04 |
110,062 |
∑ |
323,9 |
5799,3 |
37890,4 |
2129,89 |
682174,29 |
5797,302 |
Таким образом, параметры линейного уравнения регрессии составляют:
Оценка значимости параметров уравнения регрессии осуществляется при помощи t-критерия Стьюдента: если расчетные значения t-критерия больше его критической величины, то параметры уравнения признаются типичными, а сама модель адекватно описывающей зависимость между факторами.
Критическое (табличное) значение t-критерия Стьюдента определяется по приложению Б и зависит от:
– уровня значимости уравнения регрессии (α);
– числа степеней свободы: k = n − m, где m – количество параметров уравнения регрессии.
При уровне значимости α = 0,05 и числе степеней свободы k =50 − 2 =48,
табличное значение tкрит (0,05;48) = 2,0106.
Расчетные значения t-критерия определяются по формулам:
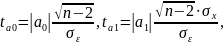
где
среднее квадратическое отклонение
результативного признака от его
выровненных значений:
Для определения среднего квадратического отклонения и оценки значимости параметров уравнения регрессии заполняется таблица 2.2.
Таблица 2.2 – Расчет средних квадратических отклонений признаков
№ предприятия |
Торговая площадь, м² |
среднесписочное число сотрудников, чел |
расчетные графы |
||
№ |
xi |
yi |
y(xi) |
(yi-y(xi))² |
(yi- |
1 |
5,9 |
124,8 |
110,062 |
217,209 |
77,687 |
2 |
5,9 |
125,1 |
110,062 |
226,141 |
83,065 |
3 |
7,8 |
134,7 |
129,404 |
28,048 |
350,214 |
4 |
6,7 |
138,8 |
118,206 |
424,113 |
520,479 |
5 |
7,8 |
130,0 |
129,404 |
0,355 |
196,392 |
6 |
6,2 |
127,0 |
113,116 |
192,765 |
121,308 |
7 |
6,1 |
94,3 |
112,098 |
316,769 |
470,283 |
8 |
7,4 |
111,4 |
125,332 |
194,101 |
21,031 |
9 |
4,3 |
94,3 |
93,774 |
0,277 |
470,283 |
10 |
6,0 |
99,6 |
111,08 |
131,790 |
268,501 |
11 |
6,2 |
127,8 |
113,116 |
215,620 |
139,571 |
12 |
6,5 |
113,2 |
116,17 |
8,821 |
7,762 |
13 |
7,3 |
122,2 |
124,314 |
4,469 |
38,614 |
14 |
6,4 |
108,7 |
115,152 |
41,628 |
53,086 |
15 |
6,6 |
105,3 |
117,188 |
141,325 |
114,191 |
16 |
7,2 |
108,7 |
123,296 |
213,043 |
53,086 |
17 |
7,0 |
113,9 |
121,26 |
54,170 |
4,351 |
18 |
6,2 |
110,2 |
113,116 |
8,503 |
33,478 |
19 |
6,6 |
102,1 |
117,188 |
227,648 |
192,821 |
20 |
7,2 |
121,1 |
123,296 |
4,822 |
26,153 |
21 |
7,3 |
112,7 |
124,314 |
134,885 |
10,798 |
22 |
6,7 |
136,8 |
118,206 |
345,737 |
433,223 |
23 |
7,6 |
115,5 |
127,368 |
140,849 |
0,236 |
24 |
7,6 |
142,1 |
127,368 |
217,032 |
681,941 |
25 |
5,6 |
104,5 |
107,008 |
6,290 |
131,928 |
26 |
7,5 |
124,5 |
126,35 |
3,422 |
72,488 |
27 |
5,8 |
100,0 |
109,044 |
81,794 |
255,552 |
28 |
4,7 |
100,9 |
97,846 |
9,327 |
227,587 |
29 |
7,3 |
124,8 |
124,314 |
0,236 |
77,687 |
30 |
6,2 |
120,1 |
113,116 |
48,776 |
16,925 |
31 |
7,6 |
130,2 |
127,368 |
8,020 |
202,038 |
32 |
6,3 |
98,6 |
114,134 |
241,305 |
302,273 |
33 |
5,9 |
92,6 |
110,062 |
304,921 |
546,905 |
34 |
5,8 |
84,1 |
109,044 |
622,203 |
1016,717 |
35 |
6,0 |
121,1 |
111,08 |
100,400 |
26,153 |
36 |
7,7 |
132,2 |
128,386 |
14,547 |
262,894 |
37 |
6,8 |
127,8 |
119,224 |
73,548 |
139,571 |
38 |
5,2 |
103,7 |
102,936 |
0,584 |
150,946 |
39 |
5,9 |
111,9 |
110,062 |
3,378 |
16,695 |
40 |
6,9 |
135,2 |
120,242 |
223,742 |
369,178 |
41 |
7,2 |
139,0 |
123,296 |
246,616 |
529,644 |
42 |
5,7 |
117,7 |
108,026 |
93,586 |
2,938 |
43 |
6,1 |
131,0 |
112,098 |
357,286 |
225,420 |
44 |
6,7 |
125,4 |
118,206 |
51,754 |
88,623 |
45 |
6,3 |
113,8 |
114,134 |
0,112 |
4,779 |
46 |
6,7 |
115,2 |
118,206 |
9,036 |
0,618 |
47 |
6,2 |
114,3 |
113,116 |
1,402 |
2,843 |
48 |
6,3 |
102,7 |
114,134 |
130,736 |
176,518 |
49 |
5,1 |
107,5 |
101,918 |
31,159 |
72,012 |
50 |
5,9 |
100,2 |
110,062 |
97,259 |
249,198 |
Сумма: |
323,9 |
5799,3 |
5797,302 |
6251,558 |
9536,680 |
)²Значит, в рассматриваемом случае:
Так как расчетные значения t-критерия больше его критической величины (30,984>2,0106; 2,0106>0,493),то параметры уравнения признаются типичными, а модель регрессии значимой для практической деятельности.
Таким образом, уравнение регрессии принимает вид:
y(xi) = 10,18 xi +50.
Теоретические значения результативного признака – грузооборот – также сводятся в таблицу 2.1.
По реальным значениям факторного и результативного признаков, представленных в таблице 2.1 на рисунке 2.1. строится поле корреляции. По выровненным (теоретическим) уровням результативного признака строится прямая уравнения регрессии.
Поле корреляции
— График уравнения регрессии y(xi) = 10,18 xi +50.
Рисунок 2.1 – Эмпирическая и теоретическая зависимости грузооборота от величины стоимости основных средств.
Положительное значение коэффициента регрессии (а1) характеризует прямую связь между признаками, то есть при увеличении стоимости основных средств грузооборот, как правило, увеличивается. Величина коэффициента регрессии свидетельствует о том, что при увеличении стоимости основных средств на 1 млн. руб. грузооборот автотранспортных предприятий в среднем увеличивается на 10,18 млн. руб.
2.2. Расчет показателей корреляции
Проверка практической значимости полученной модели регрессии между признаками осуществляется при помощи показателей корреляции.
Теснота связи между признаками в линейной модели регрессии определяется главным образом посредством расчета линейного коэффициента корреляции (r) по формуле:
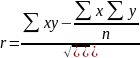
Значение коэффициента корреляции находиться в интервале от -1 до 1. Знак коэффициента корреляции, аналогично знаку коэффициента регрессии, характеризует направление связи: положительное значение – прямую связь, отрицательное значение – обратную. Величина коэффициента корреляции свидетельствует о тесноте связи: чем больше но по модулю к 1, тем связь теснее; чем ближе к 0, тем связь слабее.
Необходимые промежуточные расчеты приведены в таблице 3.1. Значит значение коэффициента корреляции составит:
Значимость коэффициента корреляции оценивается при помощи формулы:
=0,586
Так как табличное значение t-критерия Стьюдента больше его расчетного (5,01 >2,01) коэффициент корреляции признается незначимым.
Значение линейного коэффициента корреляции и индекса корреляции линейной модели, как правило, совпадают. Их значение оценивается по шкале Чеддока.
Шкала Чеддока
Показатель тесноты связи |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,999 |
Характеристика связи |
слабая |
умеренная |
заметная |
тесная |
очень тесная |
Положительный знак коэффициента индекса корреляции свидетельствует о прямой связи. Величина коэффициента индекса корреляции (0,586) характеризует связь между признаками как заметную.