1.2.2. Расчет показателей вариации

Вариация признака – это его различие внутри изучаемой совокупности. Вариация возникает вследствие влияния на характеристики единиц статистической совокупности различных факторов, сочетающихся по-разному в каждом отдельном случае. Выделяют абсолютные средние и относительные показатели вариации. Для их расчета заполняется таблица 1.4.

Таблица 1.4 – Расчет показателей вариации ряда распределения

Группы (варианты) показателей по стоимости основных средств	кол-во показателей в группе	расчетные графы
xi	fi	x'i	x'i-	|x'i- |fi	(x'i- 2*fi
4,3-4,8	2	4,55	-1,87	3,74	6,994
4,8-5,3	2	5,05	-1,37	2,74	3,754
5,3-5,8	4	5,55	-0,87	3,48	3,028
5,8-6,3	16	6,05	-0,37	5,92	2,190
6,3-6,8	9	6,55	0,13	1,17	0,152
6,8-7,3	9	7,05	0,63	5,67	3,572
7,3-7,8	8	7,55	1,13	9,04	10,215
сумма	50			31,76	29,905

Абсолютные показатели вариации характеризуют степень колеблемости признака:

– размах вариации (R) – характеризует реальный разброс значений изучаемого признака:

– среднее линейное взвешенное отклонение срединных значений вариант от их средней арифметической взвешенной определяет обобщающую характеристику распределения отклонений:

– среднее квадратическое взвешенное отклонение срединных значений вариант от их средней арифметической взвешенной определяет меру вариации.

Относительные показатели вариации характеризуют степень рассеивания индивидуальных признаков вокруг их средней арифметической величины и рассчитываются как отношение соответствующего абсолютного показателя вариации к средней арифметической:

– коэффициент осцилляции отражает степень вариации крайних значений признака относительно средней:

– относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:

– коэффициент вариации характеризует типичность средней арифметической величины:

Таким образом, величина размаха вариации и коэффициент осцилляции свидетельствуют о наличии очень большой разницы (107,07 %) между крайними значениями величины товарной площади; величины среднего и относительного линейных отклонений также устанавливают среднюю колеблемость в величине акционерного капитала (20,35 %). Так как значение коэффициента вариации (25,71 %) меньше 33,3 %, то ряд распределения признается однородным.

1.2.3. Расчет показателей формы распределения

Ряды распределения позволяют характеризовать и измерять степень колеблемости варьирующих признаков. Основные показатели формы распределения – асимметрия и эксцесс – характеризуют степень отклонения реального рассматриваемого ряда распределения от нормального распределения.

Для расчета показателей формы распределения строится таблица 1.5.

Таблица 1.5 – Расчет показателей формы ряда распределения

группы (варианты) показателей по вел-не торговой площади, м2	кол-во показателей в группе	расчетные графы
xi	fi	x'i	x'i -	(x'i - )3*fi	(x'i - )4*fi
4,3-4,8	2	4,55	-1,87	-13,078	24,457
4,8-5,3	2	5,05	-1,37	-5,143	7,046
5,3-5,8	4	5,55	-0,87	-2,634	2,292
5,8-6,3	16	6,05	-0,37	-0,810	0,300
6,3-6,8	9	6,55	0,13	0,020	0,003
6,8-7,3	9	7,05	0,63	2,250	1,418
7,3-7,8	8	7,55	1,13	11,543	13,044
сумма	50			-7,852	48,558

Асимметрия – показатель отклонения реального распределения от нормального в правую или левую сторону.

Симметричным считается распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Симметричные распределения характеризуются соотношением:

Значение показателя асимметрии может быть как положительным, так и отрицательным и характеризовать направление отклонения. Положительная величина показателя свидетельствует о правосторонней асимметрии, и при этом соблюдается следующее соотношение:

Левостороннюю асимметрию характеризуют отрицательное значение показателя и соотношение средних:

В рассматриваемом примере соблюдается соотношение правосторонней асимметрии:

6,5>6,33>6,11

Показатель асимметрии рассчитывается тремя способами:

– исходя из соотношений средних величин:

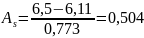
– по методу Линдберга (показатель асимметрии Линдберга):

где n – удельный вес в статистической совокупности таких предприятий, чьи индивидуальный признаки больше средней арифметической простой величины.

В рассматриваемом примере :

– с использованием центрального момента третьего порядка (μ₃ ):

Промежуточные расчеты для определения центрального момента третьего порядка осуществлены в таблице 1.5.

Тогда

Оценка степени значимости показателя асимметрии осуществляется при помощи средней квадратической ошибки, зависящей от величины статистической совокупности (n):

Если отношение больше 3, тогда асимметрия признается существенной; если меньше 3 – не существенной.

При объеме совокупности равном пятнадцати средняя квадратическая ошибка и отношение показателя асимметрии, рассчитанного с использование центрального момента третьего порядка, к ней составят:

По итогам расчета показателя асимметрии можно сделать следующие выводы. Соотношения средней арифметической и средних структурных величин, положительные значения показателей рассчитанных по методам соотношения средних свидетельствуют о правосторонней асимметрии. Отрицательное значение показателя ассиметрии рассчитанного методом Линдберга в этом случае признается незначимым.

Показатель асимметрии с использованием центрального момента третьего порядка, имеющий положительное значение, в этом случае признается незначимым.

Отношение показателя асимметрии к средней квадратической ошибке меньше 3 (1,03<3) и характеризует ее несущественность, значит распределение можно признать нормальным.

Эксцесс – показатель, который характеризует отклонение эмпирического распределения от нормального вверх и вниз. Отрицательное значение эксцесса свидетельствует о плосковершинности распределения и близости его к равномерному, положительное значение характеризует островершинность распределения и очень небольшую колеблемость признака в совокупности.

Показатель эксцесса рассчитывается двумя способами:

– по методу Линдберга (показатель эксцесса Линдберга):

Ех = n − 0,389,

где n – удельный вес количества наблюдений, находящихся в интервале, равном половине среднего квадратического отклонения вправо и влево от средней арифметической простой величины: .

В рассматриваемом случае:

– с использованием центрального момента четвертого порядка μ₄ :

Необходимые значения рассчитаны в таблице 2.4. Тогда показатель эксцесса составит:

Исходя из рассчитанных значений показателя эксцесса, делаются выводы.

Отрицательное значение показателя эксцесса рассчитанного по с использованием центрального момента четвертого порядка характеризует наблюдаемое распределение как плосковершинное. Величина отношения показателя эксцесса к его средней квадратической ошибке меньшая 3 (0,42<3) свидетельствует о незначительности эксцесса и близости наблюдаемого распределения к нормальному. Отрицательное значение показателя эксцесса рассчитанного методом Линдберга в этом случае признается незначимым.