
- •Задание № 1
- •1. Распределение Бернулли
- •2. Распределение Пуассона
- •3. Распределение Эрланга
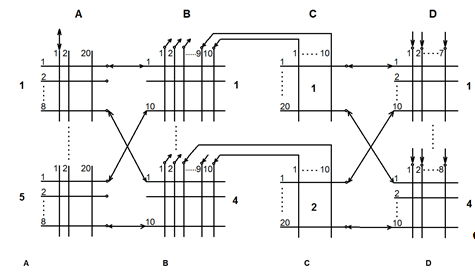
- •Структурная схема проектируемой сети
- •Функциональная схема проектируемой атс
- •Тема 4. Метод расчета пропускной способности однозвенных полнодоступных включений при обслуживании простейшего потока вызовов по системе с потерями. Первая формула Эрланга
- •Тема 5. Метод расчета полнодоступных неблокируемых включений при обслуживании примитивного потока вызовов по системе с потерями. Формула Энгсета
- •Тема 6. Методы расчета полнодоступных неблокируемых включений при обслуживании вызовов простейшего потока вызовов по системе с ожиданием
- •Тема 8. Методы расчета пропускной способности однозвенных неполнодоступных включений: упрощенная формула Эрланга, формула о’Делла, формула Пальма-Якобеуса
- •Тема 9. Метод Якобеуса для расчета пропускной способности двухзвенных полнодоступных включений.
- •Тема 10. Методы расчета пропускной способности двухзвенных схем, в выходы которых включен неполнодоступный пучок линий
- •Тема 11. Метод построения равномерных неполнодоступных включений: метод цилиндров
- •Тема 12. Метод вероятностных графов для расчета пропускной способности многозвенных коммутационных схем.
- •Тема 13. Метод расчета сети с обходными направлениями
- •1)Рассчитаем оптимальное число линий в прямых направлениях:
- •2)Рассчитаем параметры избыточной нагрузки от прямых направлений 4-2 и 4-3.
- •2) Рассчитаем параметры избыточной нагрузки от прямых направлений 4-2 и 4-3.
1)Рассчитаем оптимальное число линий в прямых направлениях:
Оптимальное число
линий в прямом направлении зависит от
интенсивности нагрузки, поступающей
на прямое направление ij
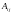 ;
;
отношения затрат на одну линию в прямом направлении к затратам на одну линию в обходном направлении
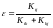 ;
;
Тогда:
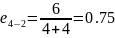
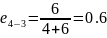
Воспользуемся
приближенным методом определения
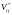 .
Как показали исследования, зависимость
.
Как показали исследования, зависимость
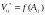 при
при
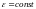 и
и
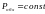 достаточно хорошо описывается уравнением
прямой
достаточно хорошо описывается уравнением
прямой
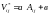 .
Значения коэффициентов а
и в
при
.
Значения коэффициентов а
и в
при
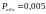 для различных
для различных
 приведены в табл. 13.1.
приведены в табл. 13.1.
Таблица 13.1
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
а |
1,162 |
1,143 |
1,132 |
1,128 |
1,124 |
1,120 |
в |
2,0 |
1,5 |
0,9 |
-0,8 |
-2,4 |
-0,5 |
Тогда:
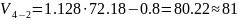
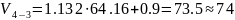 Т.к. оптимальное
число линий в прямых направлениях должно
быть кратно 30, то :
Т.к. оптимальное
число линий в прямых направлениях должно
быть кратно 30, то :
 линий.
линий.
2)Рассчитаем параметры избыточной нагрузки от прямых направлений 4-2 и 4-3.
Для характеристики
избыточной нагрузки используют два
параметра: математическое ожидание
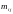 и пикфактор (коэффициент скученности)
и пикфактор (коэффициент скученности)
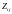 ,
определяемый отношением дисперсии
нагрузки к ее математическому ожиданию:
,
определяемый отношением дисперсии
нагрузки к ее математическому ожиданию:
 .
.
Математическое ожидание и дисперсию избыточной нагрузки можно найти из следующих выражений:
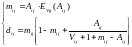 .
.
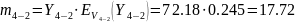
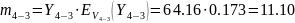
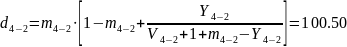
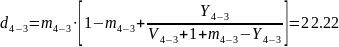
В общем случае на обходное направление могут поступать избыточные нагрузки от нескольких прямых направлений. Если принять, что поступающие на прямые направления нагрузки являются независимыми, то избыточные нагрузки будут также независимыми, и параметры объединенной на обходном направлении нагрузки определяются из выражения:
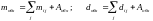
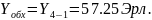
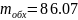

Тогда Пик-фактор
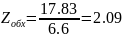
Зная значения
 и
и
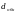 ,
находят число линий S
,
находят число линий S и
нагрузку
и
нагрузку
 ,
используя формулы полученные Раппом:
,
используя формулы полученные Раппом:
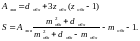
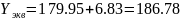 Эрл.
Эрл.

рассчитаем
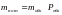 =0.43
=0.43
с помощью таблиц
Пальма по значениям
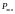 и
и
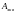 определим
определим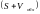 =
211
=
211
рассчитаем число линий в обходном направлении
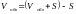 =211-102=109
=211-102=109
Вариант с учётом
2) Рассчитаем параметры избыточной нагрузки от прямых направлений 4-2 и 4-3.
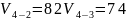
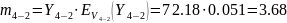
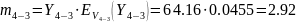


В общем случае на обходное направление могут поступать избыточные нагрузки от нескольких прямых направлений. Если принять, что поступающие на прямые направления нагрузки являются независимыми, то избыточные нагрузки будут также независимыми, и параметры объединенной на обходном направлении нагрузки определяются из выражения:
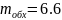
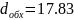
Тогда Пик-фактор

Зная значения и , находят число линий S и нагрузку , используя формулы полученные Раппом:
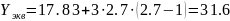

рассчитаем =0.033
с помощью таблиц Пальма по значениям и определим = 43
рассчитаем число линий в обходном направлении
=43-28=15
Размещено на Allbest.ru

