Тема 10. Методы расчета пропускной способности двухзвенных схем, в выходы которых включен неполнодоступный пучок линий
1. Для заданного в
таблице 6.2 задания 6 двухзвенного блока
ГИ методом Якобеуса рассчитаем число
линий в НПД пучке для направления от
АТСК-3 к проектируемой АТСЭ-4 при величине
и качестве обслуживания
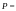5‰.
Интенсивность поступающей на один вход
блока ГИ нагрузки взять из задания 6.
,
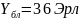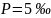
Уравнения для коммутационных двухзвенных схем с расширением:
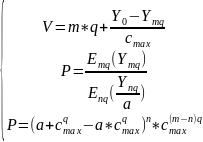
Найдем методом
подбора, с использованием таблиц Пальма,
и при известных Р,m,n,q
и a,
из второго уравнения системы определим
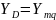
Пусть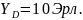
Тогда:
Не подходит по потерям.
Возьмем
:
-
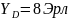выбрано верно.
Найдем решением
третьего уравнения
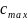
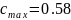
Подставим полученные значения в первое уравнение и определим число линий:
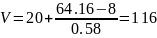
Для этого же блока ГИ методом эффективной доступности рассчитаем число линий для направления от АТСК-3 к проектируемой АТСЭ-4 при величине и качестве обслуживания 5‰.
Минимальная доступность
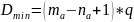
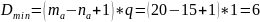
Минимальная доступность
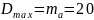
Найдем математическое ожидание количества свободных линий:
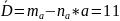
Найдем эффективную доступность:
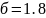
Сравнение этих методов, показывает, что метод Якобеуса даёт небольшие погрешности при расчёте числа линий в НПД пучке.
Задание № 11
Тема 11. Метод построения равномерных неполнодоступных включений: метод цилиндров
Построим схему
равномерного НПД включения линий для
направления от АТСК-3 к проектируемой
АТСЭ-4 на выходе двухзвенного блока ГИ.
Для оценки выполненного включения
составим матрицу связности. Число линий
V
возьмём из результатов расчета задания
9, число нагрузочных групп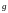
выберем таким образом, чтобы выполнялось
условие
=2÷4.
Исходные данные: =18, V=120, D = 20, =3 – коэффициент уплотнения.
Решение:
Построим матрицу связности.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
X |
2 |
2 |
3 |
3 |
3 |
1 |
4 |
|
1 |
1 |
2 |
|
1 |
3 |
2 |
1 |
2 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
3 |
|
1 |
1 |
2 |
|
2 |
3 |
3 |
2 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
3 |
|
2 |
1 |
2 |
1 |
1 |
1 |
1 |
4 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
2 |
|
2 |
1 |
2 |
1 |
2 |
2 |
5 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
2 |
|
1 |
1 |
2 |
|
2 |
6 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
2 |
|
1 |
1 |
2 |
1 |
7 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
2 |
|
2 |
1 |
2 |
8 |
4 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
2 |
|
2 |
|
9 |
|
3 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
2 |
|
1 |
10 |
1 |
|
3 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
3 |
3 |
1 |
3 |
|
11 |
1 |
1 |
|
2 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
3 |
4 |
3 |
1 |
3 |
12 |
2 |
1 |
2 |
|
2 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
3 |
3 |
3 |
3 |
3 |
1 |
13 |
|
2 |
1 |
2 |
|
2 |
1 |
3 |
3 |
3 |
2 |
3 |
X |
3 |
2 |
3 |
3 |
3 |
14 |
1 |
|
2 |
1 |
1 |
|
2 |
1 |
3 |
3 |
3 |
3 |
3 |
X |
2 |
2 |
3 |
3 |
15 |
3 |
2 |
1 |
2 |
1 |
1 |
|
2 |
1 |
3 |
4 |
3 |
2 |
2 |
X |
2 |
2 |
4 |
16 |
2 |
3 |
1 |
1 |
2 |
1 |
2 |
|
2 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
2 |
17 |
1 |
3 |
1 |
2 |
|
2 |
1 |
2 |
|
3 |
1 |
3 |
3 |
3 |
2 |
2 |
X |
2 |
18 |
2 |
2 |
1 |
2 |
2 |
1 |
2 |
|
1 |
|
3 |
1 |
3 |
3 |
4 |
2 |
2 |
X |
1
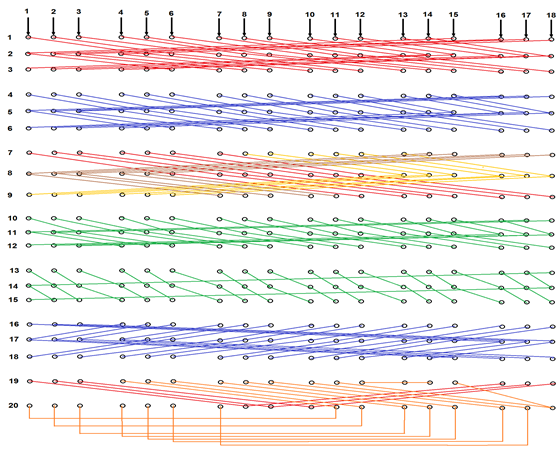
Рис. 12
Задание № 12