Тема 8. Методы расчета пропускной способности однозвенных неполнодоступных включений: упрощенная формула Эрланга, формула о’Делла, формула Пальма-Якобеуса

1.Рассчитаем и построим зависимости числа линий V и коэффициента среднего использования от интенсивности поступающей нагрузки А при величине потерь , используя метод О’Делла.

Формула О’Делла:

Где - нагрузка, обслуженная ПД пучком из D линий при потерях P.

Таблица 8.1

Направление связи от АТСЭ-4	А, Эрл
		V			V			V
УСС	6.06	14	0.428		-	-		-	-
АМТС	21.22	38	0.558		33	0.643		-	-
ЦПС	6.06	14	0.428		-	-		-	-
IP-сеть	3.03	-	-		-	-		-	-
АТСЭ – 1	57.25	98	0.584		79	0.724		74	0.774
АТСДШ – 2 (удвоен.)	144.36	241	0.599		190	0.76		172	0.839
АТСК – 2 (удвоен.)	128.32	215	0.596		170	0.754		154	0.833
АТСЭ–4 (внутристанционное)	73.18	124	0.59		100	0.732		92	0.795

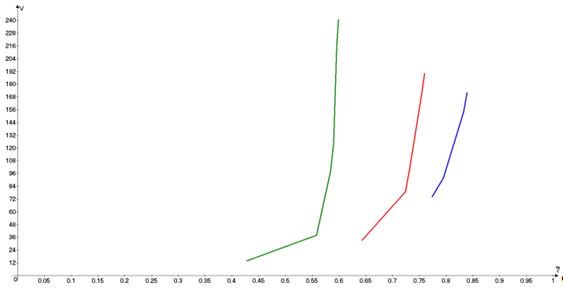
Рис. 9

2. Рассчитаем и построим зависимость числа линий от величины потерь неполнодоступного пучка при значении и по формуле Эрланга, О’Делла, Пальма – Якобеуса. Результаты расчета представить в виде таблицы и графика.

Таблица 8.2

№ п.п.		, рассчитанное по формулам
		Эрланга	О’ Делла	Пальма –Якобеуса
1 2 3 4 5	0,001 0,007 0,01 0,1 0,2	147 121 116 93 89	148 124 120 97 92	150 130 125 100 95

Формула Эрланга:

Формула О’Делла:

Формула Пальма-Якобеуса:

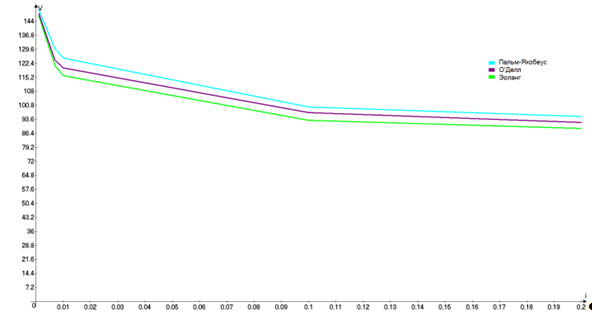
Рис. 10

Задание № 9

Тема 9. Метод Якобеуса для расчета пропускной способности двухзвенных полнодоступных включений.

Тип блока: Двухзвенный блок ГИ с параметрами

Нагрузка:

Рис. 11

Найдем количество коммутаторов в звене А:

Определим количество входов в каждом коммутаторе:

Количество выходов:

Звено А состоит из четырех коммутаторов

Рассмотрим звено В:

Количество выходов:

1)Рассчитаем величину вероятности потерь для направлений к УСС и АМТС при полнодоступном двухзвенном включении линий:

Найдем связность блока:

Найдем коэффициент сжатия или расширения:

Интенсивности нагрузок:

Норма потерь:

Вероятности потерь для направлений

к АМТС:

Возьмем q=1

- не удовлетворяет норме, тогда

Возьмем q=2

– Потери удовлетворяют нормам.

к УСС: Возьмем q=1

– Потери удовлетворяют нормам.

2) Для того же двухзвенного блока ГИ найдём необходимое число линий в направлении от АТСК-3 к проектируемой АТСЭ-4, при потерях P=0.007 и предполагая полнодоступное включение.

Найдем необходимое число линий методом подбора.

Возьмем q=1

q=3

q=4

q=5

Следовательно, нам нужно 100 линий в направлении от АТСК-3 к проектируемой АТСЭ-4.

Задание № 10