
- •11. Простые и составные числа. Бесконечность множества простых чисел. Каноническое разложение составного числа.
- •12. Сравнимость целых чисел по числовому модулю. Кольцо классов вычетов. Сравнения и их основные свойства. Полная и привидённая система вычетов.
- •13. Линейные сравнения с одним неизвестным. Различные методы их решения. Теоремы Эйлера и Ферма.
- •14. Кольцо многочленов от одной переменной. Делимость в кольце многочленов.
- •15. Приводимые и неприводимые многочлены над различными полями.
- •16. Корни многочлена. Теорема о количестве комплексных корней многочлена.
15. Приводимые и неприводимые многочлены над различными полями.
О1: Мног. полож. степени f(x)P[x] наз. приводимым над полем Р, если его м. представить в виде произв. 2х мног. полож. степени, но меньшей степ. f(x).
О2: Мног. полож. степени f(x)P[x] наз. неприводимым над полем Р, если его нельзя представить в виде произв. 2х мног.в пол. ст. из того же кольца, но меньшей степени f(x).
Пр-ры:1. f(x)=2x-3 – непривод. 2. f(x)=x2-5x+6=(x-2)(x-3) – привод над Q, R, C
Свойства приводимых и не приводимых над полем многочленов
1. Мног-ны 1й степени
неприводимы над люб. полем.Док-во: для
поля компл многочленов.
![]() .
.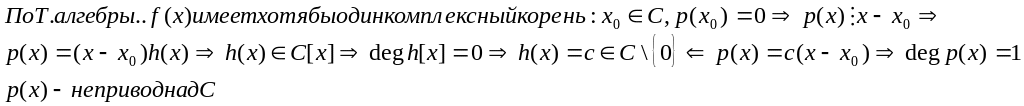 2.
Если мног. p(x)
неприводим над полем Р и p(x):f(x),
f(x)P[x],
deg
f(x)>0
тогда мног.f(x)
и p(x)
ассоциированные, т.е. p(x)=c*f(x),
cP\{0}.
3. Если мног. p(x)
неприводим над полем P
и с – не 0-ой эл. поля P[x],
то и мног. c*f(x)
– неприводим над полем P.
2.
Если мног. p(x)
неприводим над полем Р и p(x):f(x),
f(x)P[x],
deg
f(x)>0
тогда мног.f(x)
и p(x)
ассоциированные, т.е. p(x)=c*f(x),
cP\{0}.
3. Если мног. p(x)
неприводим над полем P
и с – не 0-ой эл. поля P[x],
то и мног. c*f(x)
– неприводим над полем P.
4. Пусть мног.p(x)P[x] неприводим над пол. Р и f(x) – мног.пол. ст. над полем P, тогда либо мног. f(x) и p(x) взаимно просты, либо f(x):p(x). 5. Если произвед. 2х мног. f(x) и g(x) делится на неприводимый мног. p(x)P[x] и f(x),g(x)P[x], то хотя бы 1 из мног. f(x) или g(x) делится на p(x).О3: Представление мног. f(x) в виде f(x)=p1α1(x)* p2α2(x)*…* pkαk(x) наз.каноническим разложением f(x).
Т (о не действит.корнях мног. с действит. коэфф.): Пусть f(x) мног.полож. ст.с действ. коэфф., тогда если не действ. число явл. корнем мног.f(x), то сопряженное к нему также является корнем многочлена f(x).
Т (о неприводимых над полем действительных чисел многочленах): Неприводимыми над полем R чисел явл. только лишь мног.1ой ст. и 2 не имеющие R корней.
16. Корни многочлена. Теорема о количестве комплексных корней многочлена.
Корни многочлена.
Корень многочлена
![]() над полем k — элемент
над полем k — элемент
![]() , который после подстановки его вместо
x обращает уравнение
, который после подстановки его вместо
x обращает уравнение
![]()
в тождество.
Если c является корнем многочлена p(x), то p(x) делится без остатка на x − c (теорема Безу).
Л1.(о ДОС. Модулем м-на своего наименьшего значения).
Пусть
![]() ,
такоеа что
,
такоеа что
![]()
Л2.Деламбера.
Пусть
![]() мно-н с компл переменными
мно-н с компл переменными
![]() .тогда
для
.тогда
для
![]() такое,что
такое,что
![]() .
.
О.Поле Р называется алгебраически замкнутым,если всякий мно-н полож степ.над полем Р имеет хотя бы один корень принадлеж.полю Р.
Т(основная Т. алгебры): Всякий мног. полож. ст-ни с компл. коэф. имеет хотя бы один комплексный корень.(алгебраически замкнуто)
Д-во:![]()
Мы учтем, что
![]() -корень
данного м-на.Согласно Л2 для этого числа
-корень
данного м-на.Согласно Л2 для этого числа
![]() последнее
противоречит лемме 1.
последнее
противоречит лемме 1.
Сл1.о непривод над полем компл. Мно-в.
Непривод над полем компл чисел яв-ся только многочлены первой степ.
Док-во:
Сл2(о факториальности кольца многочленов от x над полем комплексных чисел): Кольцо многочленов от x над полем комплексных чисел является факториальным кольцом (всякий многочлен положительной степени с комплексными коэффициентами можно представить в виде произведения неприводимых над полем комплексных чисел многочленов и притом однозначно с точностью до порядка следования сомножителей).
Сл 3.Всякий многочлен полож степ n с компл коэф имеет n-корней считая каждый корень столько раз какова его кратность.
Т(Виета): Пусть f(x) мног. с компл.коэф-ми полож. n-ой ст. вида f(x)=xn+a1xn-1+a2xn-2+…+an и x1, x2,…, xn корни f(x), тогда a1=-(x1+x2+…,+xn), a2=x1x2+x1x3+…+x1xn+…+xn-1xn, a3=-(x1x2x3+x1x2x4+…+x1xn-1xn+…+xn-2xn-1xn) ……. an=(-1)n x1x2…xn.
Т(о рац. корнях мног.): Пусть рац. число p/q явл.я корнем мног.f(x) полож. степ. с цел. коэфф., тогда p явл. делителем своб. Чл., а q явл. дел-ем старш. коэф-та мног. f(x).
