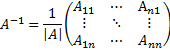- •1.Бинарные отношения. Отношение эквивалентности и разбиение множества на классы эквивалентности. Отношение порядка. Фактор-множество.
- •2.Группа. Примеры групп. Простейшие свойства групп. Подгруппы. Гоморфизмы и изоморфизмы групп.
- •2.2 Свойства групп:
- •3. Законы сокращения:
- •3. Сравнимость элемента группы по подгруппе. Нормальный делитель группы. Факторгруппы.
- •4. Кольцо. Примеры колец. Простейшие свойства колец. Подкольцо. Идеалы кольца.
- •5. Кольцо целых чисел. Теорема о делении с остатком в кольце целых чисел. Наибольший общий делитель и наименьшее общее кратное двух целых чисел.
- •6. Поле. Простейшие св-ва полей. Пр-ры полей.
- •7. Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними. Тригонометрическая форма комплексного числа.
- •Теорема об алгебраической форме комплексного числа
- •Арифметические действия над комплексными числами в алгебраической форме
- •Умножение, деление, возведение в степень комплексных чисел в тригонометрической форме.
- •Извлечение корня.
- •8. Матрицы. Операции над матрицами. Свойства операций. Матричная алгебра.
Извлечение корня.
0: К.Ч ![]() назыв. корнем n
– ой степени из К. Ч z,
если
назыв. корнем n
– ой степени из К. Ч z,
если ![]()
Теорема:
Пусть ![]() .
Тогда корень n
–ой степени из К.Ч z
имеет: 1) одно значение равное 0, если z=0
2) n
– различных значений если
,
причем если
.
Тогда корень n
–ой степени из К.Ч z
имеет: 1) одно значение равное 0, если z=0
2) n
– различных значений если
,
причем если
![]() то
то![]()
8. Матрицы. Операции над матрицами. Свойства операций. Матричная алгебра.
п.1. Матрицы. Некоторые виды матриц.
Пусть
![]() , m, n
, m, n
![]()
![]() .
.
Определение 1: всякая прямоугольная таблица из m × n действительных чисел, расположенных в m ее строках и в n ее столбцах, называется матрицей размера m × n над полем R .
 aij
R ; i=1,…,m;
j=1,…,n;
aij
R ; i=1,…,m;
j=1,…,n;
MatnR – множество квадратных матриц размера n на n с действительными элементами.
Matm.n R – множество квадратных матриц размера m на n с действительными элементами.
Определение 2: Матрица, у которой число строк и столбцов равно n, называется квадратной n-ого порядка.
Matn .
Определение 3: Совокупность элементов а11, а22, a33, …, а nn MatnR называется главной диагональю данной матрицы. Совокупность элементов а1,n, а2,n-1, a3,n-2, …, а m,1 MatnR называется побочной диагональю данной матрицы.
Определение 4: Матрицы, у которых все элементы равны нулю, называется нулевой матрицей.
Определение 5: Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной матрицей.
Определение 6: Квадратная матрица, у которой на главной диагонали расположены единицы, а вне ее – нули, называется единичной матрицей. Единичная матрица – один из примеров диагональной матрицы.
Определение 7: Квадратная матрица, у которой выше (ниже) главной диагонали расположены нули, называется нижней (верхней) треугольной матрицей.
Определение 8: Две матрицы называются равными, если у них равны соответствующие элементы.
п.2. Элементарные (эквивалентные) преобразования матриц. Ступенчатая матрица.
Определение 9: Элементарные (эквивалентные) преобразования матрицы называются следующие преобразования:
перестановка местами любых двух строк матрицы;
умножение любой строки матрицы на любое действительное число, отличное от нуля;
прибавление к любой строке матрицы любой другой, умноженной на любое действительное число;
вписывание или удаление строки, состоящей из нулей.
Определение 10: Две матрицы называются эквивалентными, если одна получена из другой с помощью какого-нибудь элементарного преобразования или их цепочки.
А~В
Предложение: Бинарное отношение «быть эквивалентными матрицами», заданное на каком-нибудь множестве матриц, является отношением эквивалентности на этом множестве.
Определение 11: Ведущим элементом строки матрицы называется первый ее ненулевой элемент.
Определение 12: Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:
все нулевые строчки матрицы (если они есть) расположены ниже ненулевых строк;
если в какой-то строке ведущий элемент расположен на k месте, то во всех следующих строках матрицы первые k элементы раны нулю.
Теорема (о приводимости матрицы к ступенчатому виду):
Всякую матрицу с помощью элементарных преобразований строк (столбцов) можно привести к ступенчатому виду.
Матрицы и операции над ними.
Умножение матриц на действительные числа.
А
![]() Matm.nR
Matm.nR
Определение1: Произведение матрицы А Matm.nR на действительное число α называется матрица αА Matm.nR, элементы которой равны произведению соответствующих элементов матрицы А на действительное число α.
Правило умножения матрицы на число:
Для того чтобы умножить матрицу на действительное число, нужно каждый элемент данной матрицы умножить на это число.
Основные свойства умножения числа на матрицу:
1*А = А;
0*А =
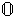 ;
;(–1)*А = – А ;
(αβ)А = α(βА);
Эти свойства верны для
![]() А
Matm.nR
,
α,β
R.
А
Matm.nR
,
α,β
R.
Сложение матриц.
А, В Matm.nR
Определение2: Суммой матриц А и В одного и того же размера называется матрица, обозначаемая А + В, элементы которой равны сумме соответствующих элементов матриц А и В.
Следствие: Складывать можно матрицы только одних и тех же размеров.
Правило сложения матриц: Для того чтобы сложить две матрицы одинаковых размеров, нужно сложить соответствующие элементы этих матриц.
А + В = В + А;
А + (В + С) = (А + В) + С;
А + = А;
А + (–А) = ;
(α + β)А = αА + βА;
α(А + В) = αА + αВ;
для А, В, С Matm.nR , α,β R.
Умножение матриц.
Пусть А Matm,kR , В Matk.nR.
Определение3: Произведением А и В называется матрица, обозначаемая как
С Matk.nR, С = АВ, элементы которой находятся по правилу:
cij = ai1b1j + ai2b2j + … + aikbkj .
Правило умножения матриц:
Для того чтобы найти элемент cij матрицы С, нужно элементы i строки матрицы А умножить на соответствующие элементы j столбца матрицы В и полученные результаты сложить.
А(ВС) = (АВ)С;
а) А(В + С) = АВ + АС;
b) (А + В)С = АС + ВС;
α(АВ) = (αА)В = А(αВ);
АЕ = ЕА = А, если А, Е MatnR;
для А, В, С Matm.nR , α,β R.
Теорема1: Множество всех матриц размера m на n Matm.nR есть аддитивная коммутативная группа.
< Matm.nR , + >
Теорема2: Множество матриц Matm.nR является векторным пространством над полем R относительно сложения матриц и умножения матриц на действительное числа.
Теорема3: Множество квадратных матриц MatnR является кольцом с единицей.
Определители и их свойства.
п.1. Определитель n-ого порядка.
Определение1: Пусть А = (а11), где А – матрица. Тогда определитель матрицы А называется число а11.
Определение2: Пусть
![]() ,
,
![]() .
.
Тогда определителем матрицы А называется число, равное |А| = а11а22 – а21а12.
Определение3:Пусть
 ,
,
![]()
Тогда определитель матрицы А есть число, равное
|А| = а11а22а33 + а12а23а31 + а13а21а32 – а13а22а31 – а11а23а32 – а12а21а33.
Определение4: Пусть
 ,
,
![]()
Определителем матрицы А называется сумма n! слагаемых, содержащих n сомножителей, взятых по одному и только одному из каждой строки и каждого столбца матрицы А, причем произведению приписывается знак «+», если подстановка, составленная из индексов сомножителей является четной и знак «–», если такая подстановка является нечетной.
п.2. Свойства определителя.
Если в определителе матрицы n-ого порядка имеется строчка или столбец из нулей, то такой определитель равен нулю.
Определитель диагональной матрицы равен произведению элементов главной диагонали.
Определитель треугольной матрицы равен произведению элементов главной диагонали.
Определение5: Матрицей, транспонированной к матрице А, называется такая матрица, которая получена из матрицы А заменой строк соответствующими столбцами.
Определители матрицы А и транспонированной к ней матрицы Ат равны.
Если в определителе поменять местами какие-нибудь две строчки, то знак определителя изменится на противоположный.
Если в какой-то строке определителя матрицы есть общий множитель, то его можно вынести за знак определителя.
Определитель матрицы, содержащий две одинаковые строчки, равен нулю.
Если в определителе матрицы имеются две пропорциональные строчки, то определитель матрицы равен нулю.
Если в определителе матрицы есть строка, в которой каждый элемент есть сумма двух слагаемых, то такой определитель равен сумме двух определителей, у которых все строчки такие же, как у данного, кроме строки, где каждый элемент есть сумма двух слагаемых. В первом определителе в этой строке будут расположены первые слагаемые, а во втором в этой строчке – вторые слагаемые.
Определитель матрицы не изменится, если к какой-то строке прибавить любую другую строчку, умноженную на какое-то действительное число.
Если в определителе матрицы какая-то строка есть линейная комбинация других строк, то этот определитель равен нулю.
Определитель матрицы не изменится, если к какой-то строке прибавить линейную комбинацию других строк.
Разложение определителя по элементам строки (столбца).
п.1. Минор и алгебраическое дополнение элемента определителя.
Пусть есть Δ – определитель n-ого порядка.

Определение1: Минором элемента
аij
![]() Δ называется определитель из определителя
, вычеркиванием i-той
строки и j-ого столбца.
Δ называется определитель из определителя
, вычеркиванием i-той
строки и j-ого столбца.
Определение2: Алгебраическим дополнением элемента аij Δ называется минор этого определителя, взятый со знаком (-1)i+j.
Aij = (-1)i+j Mij.
Теорема1(о каждом члене произведения элемента определителя на его алгебраическое дополнение):
Каждый член произведения аijAij является членом определителя Δ с тем же самым знаком.
п.2. Разложение определителей по элементам строки (столбца).
Теорема2(об определителе, у которого все элементы какой-то строки равны нулю кроме одного):
Если в определителе Δ все элементы i-ой строки равны нулю, кроме элемента аij, то этот определитель Δ равен произведению этого ненулевого элемента на его алгебраическое дополнение.
Δ = аijAij.
Док-во: Все члены в определителе, кроме быть может одного аij равны нулю. Если записать произведение всех членов определителя, то, выделив член аij, а остальное произведение будет являться его дополнением, и по теореме 1, является членом определителя с тем же знаком, значит Δ = аijAij.
Теорема3(о разложении определителя по элементам строки(столбца)):
Какую бы строчку (столбец) определителя Δ мы не взяли он (определитель) равен сумме произведений элементов этой строки на их алгебраические дополнения.
Теорема4(о сумме произведений элементов строки(столбца) на алгебраические дополнения соответствующих элементов другой строки):
Сумма произведений элементов какой-нибудь строки(столбца) определителя на алгебраические дополнения соответствующих элементов другой строки определителя равна нулю.
Обратные матрицы.
п.1. Обратная матрица. Обратимая матрица.
Определение1:
Пусть А, В MatnR.
Матрица В называется обратной к матрице А, если А*В = В*А = Е, где Е – единичная матрица.
Определение2: Матрица А называется обратимой, если существует матрица обратная ей.
Теорема1(о единственности обратной матрицы):
Если матрица А является обратимой, то для нее существует единственная ей обратная матрица.
Док-во: допустим, что для матрицы А есть две обратные матрицы А1 и А2. Тогда
![]()
Теорема2(об определителе произведения матриц):
Определитель произведения квадратных матриц одного порядка равно произведению определителей данных матриц.
|А*В| = |А|*|В| ,где А,В MatnR.
Определение3: Матрица А называется невырожденной, если ее определитель не равен нулю, и вырожденной, если определитель равен нулю.
Теорема3(критерий обратимости матрицы):
Матрица А является обратимой тогда и только тогда, когда она является невырожденной, то есть ее определитель не равен нулю.