7. Транспортная задача

Среди задач линейного программирования особое место занимает транспортная задача. Ее методы широко используются в экономике и бизнесе, особенно в транспортных и дистрибьютерских фирмах.

Традиционная постановка транспортной задачи такова:

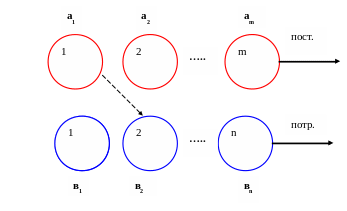
Рис. 3

Имеются m поставщиков и n потребителей. У поставщиков сосредоточен однородный груз в количестве a₁, a₂,…..a_m.

Спрос потребителей на груз: в₁, в₂,….в_n.

Известны стоимости (тарифы) с_ij на перевозку единицы груза от i-го поставщика к j- му потребителю.

Требуется составить оптимальный план перевозок грузов такой, чтобы:

1. вывести весь груз поставщиков

2. удовлетворить весь спрос потребителей

3. минимизировать суммарные затраты на перевозку.

Построение математической модели:

Пусть х_{ij –} количество груза, перевозимого от i-го исх. пункта к j-му пункту потребления.

х₁₁ + х₁₂+ ….+х_1n= а₁

х₂₁ + х₂₂+ ….+х_2n= а₂ →все грузы должны быть вывезены

……………………..

х_m1 + х_m2+ ….+х_mn= а_m

х₁₁ + х₂₁+ ….+х_m1= b₁

х₁₂ + х₂₂+ ….+х_m2= b_{2 →} весь спрос удовлетворен

…………………….

х_1n + х_2n+ ….+х_mn= b_n

Замечание:

Если , то задача называется закрытой, в противном случае - открытой. Доказано, что закрытая транспортная задача всегда имеет оптимальное решение.

8. Метод потенциалов решения транспортной задачи

Разберем этот метод на конкретном примере:

На трех железнодорожных станциях сосредоточено топливо для пяти заводов. Необходимо составить оптимальный план перевозок топлива. Исходные данные заданы в транспортной таблице стандартного вида:

Потр.	1	2	3	4	5	ЗАПАСЫ
Пост.
1	7	4	2	3	4	200
2	6	4	5	2	7	250
3	5	8	3	5	9	50
СПРОС	100	70	80	150	100

Задача закрытая (почему?).

1. Нахождение начального опорного плана (угловой точки).

Используется метод минимальной стоимости. Его суть:

а) находим клетку с минимальной стоимостью и в максимально возможной степени удовлетворяем спрос соответствующего потребителя. Результат записываем в левый нижний угол клетки.

Потр.	1	2	3	4	5	ЗАПАСЫ
Пост.
1	7 20	4	2 80	3	4 100	0
2	6 30	4 70	5	2 150	7	0
3	5 50	8	3	5	9	0
СПРОС	0	0	0	0	0

б) правило: “там, где 0 вычеркиваем”

в) среди всех невычеркнутых клеток вновь находим клетку с минимальной стоимостью и вновь повторяем алгоритм.

в) контроль: общее число занятых клеток равно m + n- 1

г) F = 20*7 + 80*2+ 100*4 + 30*6 + 70*4 + 150*2 + 50*5= 1710

Начальный опорный план - в левом нижнем углу клеток.

2. Проверка опорного плана на оптимальность.

Проверка на оптимальность осуществляется с помощью потенциалов во вновь составленной таблице.

Постр.	1	2	3	4	5	U
Пост.
1	7 20	4 +	2 80	3	4 100	0
2	6 30	4 70	5	2 150	7	-1
3	5 50	8	3	5	9	-2
V	7	5	2	3	4

ПРАВИЛО 1: для всех занятых клеток должно быть:

u _i + v _j = c _{i j} (1)

(сумма потенциалов равна стоимости)

ПРАВИЛО 2: для всех свободных клеток должно быть:

u _i + v _j ≤ c _{i j} (2)

Условие оптимальности нарушено в клетке (1, 2)!

Итак, полученный опорный план не оптимален!

Экономический смысл потенциалов:

Потенциалы u и v можно рассматривать как платежи поставщиков и потребителей некоторому третьему лицу- назовем его ‘ перевозчиком”.

Формула (2) означает, что при оптимальном плане перевозок стороны не хотят переплачивать сверх установленного тарифа.

С другой стороны, перевозчик, установив оптимальный план, хочет получить максимум, т.е. весь тариф полностью (формула (1)).

3. Переход к новому опорному плану, лучшему, чем предыдущему.

Находим клетку, в которой условие оптимальности нарушено в наибольшей степени. В нашем случае это клетка (1,2). Далее

а) помечаем эту клетку знаком + и строим цикл, начинающийся и заканчивающийся в этой же клетке.

Цикл- это замкнутая ломаная линия, состоящая из горизонтальных и вертикальных отрезков, соединяющих некоторые занятые клетки.

Такой цикл всегда существует и только один!

б) размечаем вершины цикла знаками - + - … считая от исходной клетки.

в) находим, по всем клеткам, помеченным знаком - наименьшую перевозку. Обозначим ее α. У нас α = 20.

г) двигаясь по циклу, прибавляем α к клеткам со знаком + и вычитаем ее из клеток со знаком - .

Получающийся “лишний нуль” стираем.

Результаты записываем в новую таблицу.

Потр.	1	2	3	4	5	U
Пост.
1	7	4 20	2 80	3	4 100	0
2	6 50	4 50	5	2 150	7	0
3	5 50	8	3	5	9	-1
V	6	4	2	2	4

Не забываем проверять условие: число занятых клеток = m+n -1.

4. Проверка опорного плана на оптимальность.

Вновь находим потенциалы и проверяем условие (2).

Условие оптимальности выполнено.

Получен оптимальный план перевозок!

F_min = 20*4 + 80*2 + 100*4 + 50*6 + 50*4 + 150*2 + 50*5 = 1690

х₁₂ = 20

х₁₃ = 80

х₁₅ = 100

х₂₁ = 50

х₂₂ = 50

х₂₄ = 150

х₃₁= 50