4. Моделирование социально- экономической структуры общества.
Важной проблемой в социальных и экономических исследованиях является проблема измерения социального неравенства. Обычный подход социологов таков: все общество делят на три группы: богатые, средние и бедные. Если преобладают середняки, а крайние группы по численности примерно одинаковы, то делается вывод, что данное общество примерно однородно. Если же, наоборот, большая часть населения в крайних группах, то налицо сильное расслоение и неравенство.
Достижение современной экономико-математической науки - количественный подход к проблеме. Его сутъ в следующем:
Введем
функцию у (х), х
.
Здесь у (х)- доля денежных доходов общества, приходящихся на долю населения х.
Так, у(0,8) = 0,3 означает, что на 80% населения приходится 30% доходов общества; у(0,9)=0,1 означает, что 90% населения получают лишь 10% доходов общества; у(0,5)=0,5 означает, что 50% населения получают 50% доходов общества;
Функция у (х) называется функцией Лоренца.
Последний пример подсказывает, что функция у (х)=х отражает идеально справедливое общество- рис.1
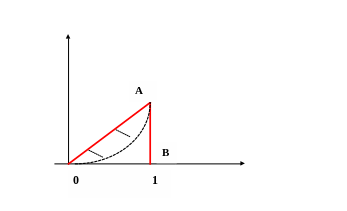
Рис. 18
В действительности же функция Лоренца имеет вид пунктирной линии выпуклой вниз (рис.1). Таким образом, чем больше площадь заштрихованной луночки, тем менее справедливым, более расслоенным является общество.
Количественно это выражают коэффициентом Джини
(Gini coefficient). Конрадо Джини (1884-1965). Он равен отношению площади луночки к площади треугольника ОАВ.
Таким образом, коэффициент Джини макроэкономический показатель, характеризующий дифференциацию денежных доходов населения.
Заметим, что в СССР 80-го года коэффициент Джини составлял 0,26, а в России 2000 года 0,44.
Пример.
Для некоторой страны функция Лоренца имеет вид:
у
(х) =
.
Найдем коэффициент Джини:
21. Дисперсионный анализ
(Analysis of Variance )- ANOVA
В практической деятельности менеджеров, руководителей производств, экономических и кадровых служб часто возникает необходимость убедиться - действительно ли данный качественный фактор А оказывает существенное, значимое влияние на некоторый результативный признак.
Например, влияет ли тип станка на среднюю производительность рабочих, влияет ли температура на средний срок службы данной установки, влияет ли тот или иной месяц года на средний объем реализации продукции, влияет ли разбиение студентов на группы на их среднюю успеваемость, влияет ли размер предприятия на производительность, влияет ли численность региона на объем выручки и т.д.
Пример 1.
Служба управления персоналом крупной компании хочет проанализировать, влияет ли тип методики обучения на среднюю производительность персонала.
Построим математическую модель ситуации и воспользуемся методом математической статистики.
1. Пусть Х - случайная величина, определяющая результативный признак, в данном случае - производительность. Фактор А - методика обучения.
2. Разобьем фактор А на к уровней - рассмотрим 3 методики обучения (к = 3) и для каждого уровня получим выборку объема n случайной величины Х (n=5):
уровень |
в
ы б о р к а
|
||||||
1 |
15 |
18 |
19 |
22 |
11 |
17 |
19 |
2 |
22 |
27 |
18 |
21 |
17 |
21 |
|
3 |
18 |
24 |
16 |
22 |
15 |
19 |
|
Для
каждого уровня подсчитаем среднее
,
а также среднее
по всем выборкам:
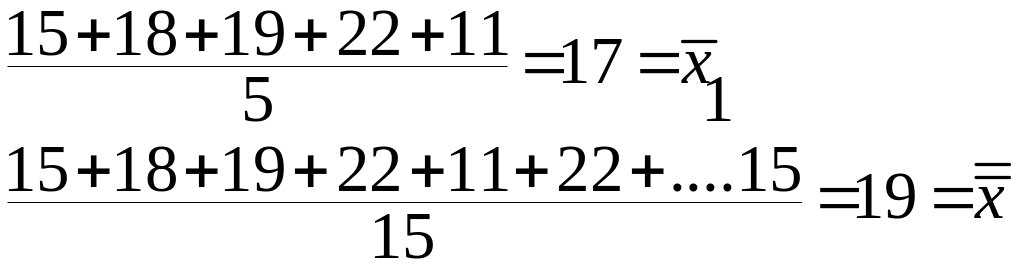
3. Подсчитываем факторную дисперсию:
( оценивает степень влияния данного фактора на результирующий признак).
QА = 5(17-19)2 + 5(21-19)2 +5(19-19)2 = 40
4. Подсчитываем остаточную дисперсию:
(оценивает влияние иных, остаточных причин на результирующий признак).
Qост = (15-17)2+ (18-17)2+ (19-17)2+ (22-17)2 + (11-17)2 +
(22-21)2+ (27-21)2+ (18-21)2+ (21-21)2 + (17-21)2 +
(18-19)2+ (24-19)2+ (16-19)2+ (22-19)2 + (15-19)2 =192
Если эти дисперсии значимо отличаются, то это свидетельствует о существенном влиянии фактора, в противном случае - принимается, что фактор не оказывает существенного влияния. С целью сравнения дисперсий
5. Вычисляем значение критерия Фишера:
Fнабл.
=
6. Выбираем уровень значимости α = 0,05
7. Находим число степеней свободы числителя (v1) и знаменателя (v2):
v1 = к – 1 =2
v2 = N– k =15 – 3=12
По таблице критерия Фишера (одна из таблиц математической статистики) находим: Fкр = 3,885
8. Так как наблюдаемое значение критерия (1,25) не превосходит критического значения (3,885), то принимается гипотеза о несущественности влияния фактора А при уровне значимости 0,05.
(в противном случае гипотезу следовало бы отвергнуть).
Итак, тип методики обучения не оказывает значимого влияния на производительность работников.
Файл ANOVA-1
Обозначения в EXCEL таблице:
SS |
df |
MS |
QA – факт. дисп. |
k - 1 |
QA/(k-1) |
Qост – остаточн. дисп. |
N - k |
Qост/(N-k) |