15. Итерационный метод (Брауна – Робинсона)
Во многих случаях решение матричных игр представляет сложный и громоздкий процесс. Кроме того, часто в практических задачах нет необходимости находить точное решение игры. Достаточно найти приближенное решение.
Рассматриваемый приближенный метод отличается достаточной простотой. Суть его в том, что матричная игра фиктивно разыгрывается несколько раз (в несколько туров), при этом накапливаются статистические данные об игре. По ним и вырабатываются рекомендации об оптимальных стратегиях игроков.
Продемонстрируем работу метода на примере:
Игра задана платежной матрицей (таблицей):
Выбирает А
Стр. В
Выбирает В
Стр. А
Ср. выигр.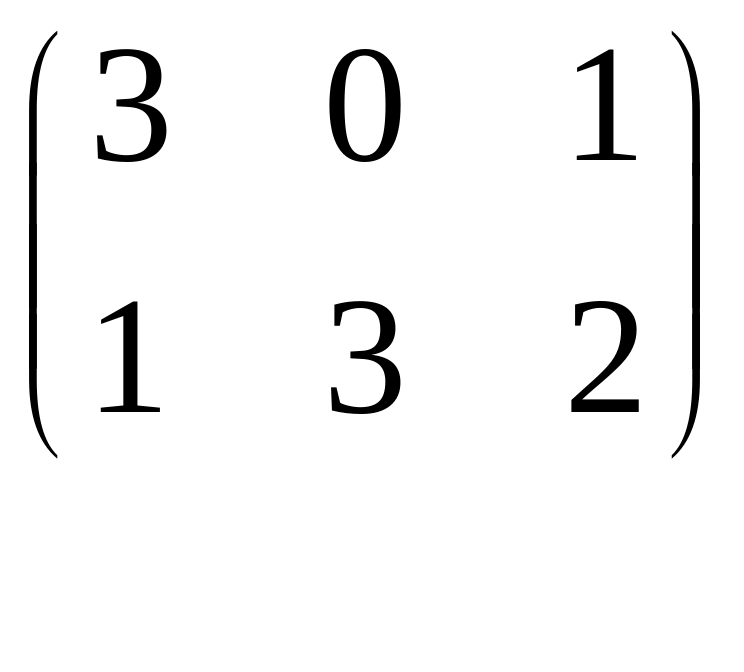
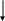
№ тура |
i |
B1 |
B2 |
B3 |
j |
A1 |
A2 |
v* |
v* |
v |
1 |
2 |
1 |
3 |
2 |
1 |
3 |
1 |
1 |
3 |
2 |
2 |
1 |
4 |
3 |
3 |
3 |
4 |
3 |
1,5 |
2 |
1,75 |
3 |
1 |
7 |
3 |
4 |
2 |
4 |
6 |
1 |
2 |
1,5 |
4 |
2 |
8 |
6 |
6 |
3 |
5 |
8 |
1,5 |
2 |
1,75 |
5 |
2 |
9 |
9 |
8 |
3 |
6 |
10 |
1,6 |
2 |
1,8 |
6 |
2 |
10 |
12 |
10 |
1 |
9 |
11 |
1,67 |
1,83 |
1,75 |
7 |
2 |
11 |
15 |
12 |
7 |
12 |
12 |
1,57 |
1,71 |
1,64 |
8 |
1 |
14 |
15 |
13 |
3 |
13 |
14 |
1,625 |
1,75 |
1,69 |
9 |
2 |
15 |
18 |
15 |
3 |
14 |
16 |
1,67 |
1,78 |
1,72 |
10 |
2 |
16 |
21 |
17 |
1 |
17 |
17 |
1,6 |
1,7 |
1,65 |
1 тур:
игрок А, естественно, выбирает 2-ю стратегию (max min). У игрока В три стратегии. Какую он выберет? Конечно 1-ю (он хочет минимизировать проигрыш!). Выделим соответствующий проигрыш. Итак, игрок В выбрал 1-ю стратегию. Отметим это в 6-м столбце.
Как же ответит А? Конечно 1-й стратегией. Выделим соответствующий выигрыш.
v* - накопленный проигрыш игрока В/ число ходов
v* - накопленный выигрыш игрока А/ число ходов
v - средний выигрыш
2 тур:
Итак, игрок А выбрал 1-ю стратегию. У игрока В накопленные проигрыши 4, 3, 3. Минимизируя свой проигрыш игрок В выберет 2-ю или 3-ю стратегию. Пусть ему приглянулась стратегия 3. Игрок А ответит либо 1, либо 2 стратегией. Его накопленные выигрыши либо 4, либо 3. Он ответит 1 стратегией, и т.д.
Вывод: после 10 туров v = 1,65. Игрок А воспользовался 1-й стратегией 3 раза- p1 = 3/10= 0,30, 2- й стратегией 7 раз - р2 = 7/10= 0,70.
Аналогично для игрока В: q1 = 1/4, q2=0, q3 =2/3.
Как видно, всего после десяти итераций можно уже судить об основных тенденциях игры.