3.Приклади
1. Розв’яжемо параболічне рівняння вигляду:
Kрайові
умови візьмемо такі: задані значення
концентрації забруднення на початку
процесу в точці
і на віддалі
від початку в точці
, а саме:
C(0,t)=
,
c(l,t)=
;
і повинна виконуватись одна з таких додаткових (початкових) умов:
,
рівняння обчислюється за такою формулою:
.
Програмно обчисливши це рівняння методом сіток ми отримали наступний результат:
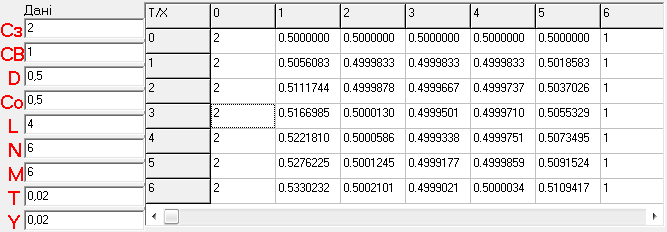
2. Розв’яжемо теж рівняння вигляду:
Але за таких крайових умов:
рівняння обчислюється за такою формулою:
.
Програмно обчисливши це рівняння методом сіток ми отримали наступний результат:
Отже, метод сіток є зручним і ефективним методом для розв’язування рівнянь такого типу.І як можемо бачити з різними крайовими умовами результати фактично збігаються.
Висновок
В даній курсовій роботі ми розглянули математичну модель у випадку нестаціонарного процесу переносу забруднень у нерухомому середовищі за відсутності джерел і хімічних або біологічних перетворень. Такий процес описується нестаціонарним рівнянням молекулярної дифузії:
Практичний
розв’язок шукаємо методом сіток. При
розв’язуванні цим методом дістаємо
різницеву схему, яка є явною, тому що
дає можливість знайти розв’язок на
шарі через розв’язок на
-
му шарі. Також слід відмітити, що схема
апроксимує задачу на розв’язку
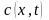з похибкою порядку
,
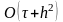тому ця схема є також і збіжною з похибкою
такого ж порядку. Остаточна формула
практичного розв’язоку має вигляд:
.
За таких крайових умов:
C(0,t)= , c(l,t)= ; , .
І такого вигляду :
.
При таких умовах:
.
Література
Лаврик В.І. Методи математичного моделювання в екології: Навчальний посібник для студентів вищих навчальних закладів. – Вид. дім „КМ Академія”, 2002-203с.
Березин И.С., Жидков Н.П. Методы вичислений М.: Физматгиз, 1960, т.2.
Гаврилюк І.П., Макаров В.Л. Методи обчислень: У – 2 ч. К.: Вища школа, 1996. ч.2.
Григоренко Я.М., Панкратова Н.Д. Обчислювальні методи К.: Вид. „Либідь”, 1995. – 280 с.
Крилов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы высшей математики. Минск: Высшая школа, 1975, т.2.