
- •9.Общее решение совместной неоднородной системы линейных алгебраических уравнений.
- •10. Определение линейного (векторного) пространства, действительного и комплексного. Простейшие свойства. Примеры линейных пространств.
- •11. Линейно зависимые и линейно независимые системы векторов. Критерий линейной зависимости. Достаточное условие линейной зависимости.
- •14. Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при изменении базиса
- •15. Определение линейного подпространства. Свойства линейного подпространства
- •16. Определение линейной оболочки системы векторов.
- •17. Сумма и пересечение подпространств. Прямая сумма подпространств.
- •18. Определение линейного оператора. Простейшие свойства. Примеры.
- •19. Матрица оператора в базисе. Примеры.
- •21. Матрица суммы операторов, произведения оператора на число и произведения операторов.
- •22. Обратный оператор для данного линейного оператора и его свойства. Критерий обратимости линейного оператора. Примеры обратимых и необратимых операторов.
- •23. Преобразование матрицы линейного оператора при изменении базиса. Подобные матрицы.
- •24. Характеристический многочлен матрицы. Характеристический многочлен линейного оператора, его инвариантность.
- •32. Определение евклидова пр-ва. Норма вектора. Неравенство Коши-Буняковского и нер-во треугольника. Угол между двумя векторами.
- •33. Ортонормированные базисы (онб) евклидова пр-ва. Теорема о существовании онб, процесс ортогонализации Шмидта.
- •34. Ортогональные матр. , их св-ва. Переход от одного онб к другому в евклидовом пр-ве.
- •35. Самосопряженные операторы в евклидовом пр-ве, их св-ва.
- •36. Спектральная теорема самосопряженного оператора
- •37. Приведение квадратичной формы к главным осям в евклидовом пространстве.
23. Преобразование матрицы линейного оператора при изменении базиса. Подобные матрицы.
[e]
= (e1,…,en)
– базис 1;
 – базис 2;
– базис 2;
Т
–матрица перехода от [e]
к
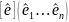 = (e1,
…, en)
T;
A
ϵ L(Vn).
= (e1,
…, en)
T;
A
ϵ L(Vn).
[e]:
A ↔ Ae;
A(e1,
…, en)
= (e1,
…, en)Ae
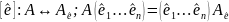
 ;
(e1,
…, en)
∙ Ae
∙
T = (e1,
…, en)T
;
(e1,
…, en)
∙ Ae
∙
T = (e1,
…, en)T
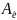 ⇔
AeT
= T ∙
;
⇔
AeT
= T ∙
;
Т.к.
det T ≠ 0, то
∃

Определение: Квадратные матрицы B и D порядка n называются подобными, если D = Q-1BQ, Q – некоторая невырожденная матрица порядка n.
Следствие 1: Подобные матрицы и только они задают один и тот же линейный оператор в различных базисах пространства Vn.
Доказательство:
Пусть [e] – базис, A ϵ L(Vn), Ae – матрица А в базисе [e]. Если
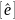 - другой базис Vn,
то
– матрица оператора А в
.
- другой базис Vn,
то
– матрица оператора А в
.
 ,
где Т – матрица перехода от [e]
к
.
Т.е. Ae
и
подобны.
,
где Т – матрица перехода от [e]
к
.
Т.е. Ae
и
подобны.
Пусть подобна Ae, т.е. ∃Q – матрица, det Q ≠ 0, такая, что
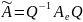 .
.
Рассмотрим
векторы
 = (e1,
…, en)Q.
В этом случае
= (e1,
…, en)Q.
В этом случае
 - линейно независимы и образуют базис,
причем Q
– матрица перехода от [e]
к
- линейно независимы и образуют базис,
причем Q
– матрица перехода от [e]
к
 ,
,
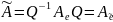 – матрица оператора А в
.
– матрица оператора А в
.
Следствие 2: Определитель матрицы линейного оператора не зависит от выбора базиса.
Доказательство: [e]: A ↔ Ae; : A ↔ ; ;
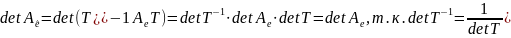 .
.
24. Характеристический многочлен матрицы. Характеристический многочлен линейного оператора, его инвариантность.
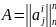 ;
λ
– произвольная переменная, E
= En.
;
λ
– произвольная переменная, E
= En.
Матрица A – λE называется характеристической матрицей матрицы А.
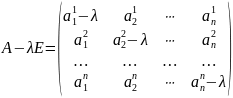
Рассмотрим многочлен:
 +
+
Определение: Многочлен det(A – λE) называется характеристическим многочленом матрицы А степени равной n. Коэффициент при λn равен (-1)n.
Теорема: Характеристический многочлен у подобных матриц совпадает.
Доказательство: Пусть матрицы B и D подобны, т.е. ∃ T (det T ≠ 0) такая, что D=T-1BT; det(D-λE) = det(T-1BT – λT-1ET) = det(T-1(B-λE)T) = det T-1 ∙ det(B-λE) ∙ det T = det(B-λE), ч.т.д.
Определение: Характеристическим многочленом оператора А называется характ. многочлен матрицы этого оператора в некотором базисе V.
Следствие: Характ. многочлен лин. оператора Vn не зависит от выбора базиса.
Доказательство:
[e]:
A
↔ Ae;
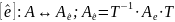 ;
(det
T
≠ 0)
;
(det
T
≠ 0)
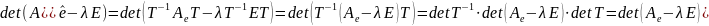
 ч.т.д.
ч.т.д.
25. Собственные значения и собственные векторы линейного оператора. Примеры. Теорема о собственных значениях линейного оператора в конечномерном пространстве. Нахождение собственных значений и координат собственных векторов.
V – линейное пространство (действительное или комплексное);
А – линейный оператор пространства V, A ϵ L(V)
Определение:
Число
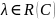 называется
собственным значением линейного
оператора А, если в пространстве V
существует ненулевой вектор x
такой, что выполняется Ax
= λx,
называется
собственным значением линейного
оператора А, если в пространстве V
существует ненулевой вектор x
такой, что выполняется Ax
= λx,
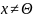
Любой вектор называется собственным вектором оператора А, соответствующим (отвечающим, принадлежащим) собственному значению λ.
Пример:
 V3
– пространство геометрических векторов
в пространстве.
V3
– пространство геометрических векторов
в пространстве.
А – оператор проектирования на XOY
①

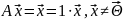
λ = 1 – собственное значение оператора
 – собственный
вектор, отвечающий данному собственному
значению.
– собственный
вектор, отвечающий данному собственному
значению.
②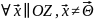
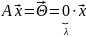 ,
λ
= 0 – собственное значение
,
λ
= 0 – собственное значение
– собственный вектор
 Тождественный
оператор
Тождественный
оператор
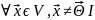 x
= x
= 1 ∙ x,
λ
= 1.
x
= x
= 1 ∙ x,
λ
= 1.O – нулевой оператор Ox = Θ = 0*x, λ = 0
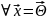 - собственный вектор
- собственный вектор
Теорема В действительном линейном пространстве Vn действительные корни характеристического многочлена оператора А и только они являются собственными значениями оператора А.
В комплексном линейном пространстве Vn все корни характеристического многочлена оператора А и только они являются собственными значениями оператора А.
Vn – n-мерное линейное пространство (ℝ или ℂ);
A ϵ L(Vn); [e] = (e1, e2, …, en) – базис;
[e]: A ↔ Ae – матрица оператора А в базисе [e].
Доказательство: det(A-λE) – характеристический многочлен; E = En;
λ0 – собственное значение А, если ∃ x ≠ 0, x ϵ Vn, такой, что Ax = λ0x;
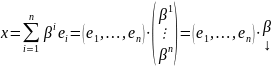
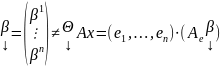 ;
;
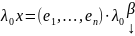 ;
;
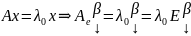 ;
;
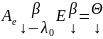 ;
;
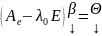 ;
;
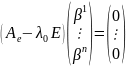
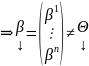 является
решением однородной СЛАУ.
является
решением однородной СЛАУ.
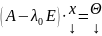
(2)

Т.к.
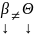 и матрица Аe
– λ0E
– квадратная порядка n,
то система (2) имеет ненулевое решение
⇔
det(Ae-λ0E)
= 0, т.е. λ0
– решение характеристического уравнения
(корень характеристического многочлена).
и матрица Аe
– λ0E
– квадратная порядка n,
то система (2) имеет ненулевое решение
⇔
det(Ae-λ0E)
= 0, т.е. λ0
– решение характеристического уравнения
(корень характеристического многочлена).
Характеристический многочлен det(A – λE):
в действительном случае рассматривает только действительные корни характеристического многочлена
в комплексном случае - характеристический многочлен имеет n корней, они являются собственными значениями.
Следствие: В комплексном линейном пространстве всякий линейный оператор имеет собственное значение и собственный вектор.
В действительном линейном пространстве, если линейная размерность четная, то линейный оператор может не иметь собственных векторов.
Нахождение собственных значений и координат собственных векторов.
Vn – линейное пространство (ℝ или ℂ); A ϵ L(Vn);
Фиксированный базис [e] = (e1, …, en);
[e]: A ↔ Ae – матрица линейного оператора А.
Ae – λE – характеристическая матрица матрицы Ae ;
Составленное характеристическое уравнение det(Ae – λE) = 0;
Решаем характеристическое уравнение и находим корни λ1, …, λn.
Последовательно берем λi(I = 1, …, n), подставляем вместо λ в характеристическую матрицу и составляем однородную СЛАУ:
(2)
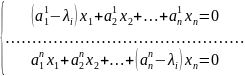
Собственные векторы, отвечающие за λi – все ненулевые решения полученной системы.
Билет 26. Свойства собственных векторов, отвечающих одному и тому же собственному значению линейного оператора. Теорема о линейной независимости собственных векторов, отвечающих попарно различным собственным значениям.
Пусть V-линейное пространство V’ V.
Определение 14. Линейное подпространство V’ V называется инвариантным относительно A, если ∀x V: Ax V’.
Теорема 9. Все собственные векторы линейного оператора A, соответствующие собственному значению λ0 вместе с θ образуют линейное подпространство V’, инвариантное относительно A.
Док-во: V’={x V: Ax = λ0x}
1) V’ – линейное подпространство ∀x1, x2 V’
A(x1+ x2 ) = Ax1 + Ax2 = λ0x1 + λ0x2 = λ0( x1 + x2 ) => x1 + x2 V’
A( μx1 ) = μAx1 = μλ0x1 = λ0( μx1 ) => μx1 V’.
Докажем
инвариантность V’
относительно A.
∀x
V’:
 т.к. V’
– линейное подпространство, следовательно
V’
инвариантно относительно A.
т.к. V’
– линейное подпространство, следовательно
V’
инвариантно относительно A.
Теорема 10. Если λ1, …, λk – различные собственные значения оператора A (т. е. λi ≠ λj, при i ≠ j ), то собственные вектора f1…, fk, отвечающие данным собственным значениям, являются линейно независимыми.
Док-во: По условию: Afi = λifi i=1, …, k.
λi ≠ λj при i ≠ j.
Ведём индукцию по k - числу векторов.
1) k = 1 – основание индукции. λ1 собственный вектор f1 ≠ θ => f1 – линейно независим.
2) Предположим, что любые(k -1) собственные векторы, отвечающие различным собственным значениям, линейно независимы.
3) Докажем утверждение для k. λ1, … ,λk-1, λk; f1, …,fk-1, fk – линейно независимы.
α1f1 + … + αk-1fk-1 + αkfk = θ; (3)
A(α1f1 + … + αk-1fk-1 + αkfk ) = Aθ = θ;
α1Af1 + … + αk-1Afk-1 + αkAfk = θ;
α1λ1f1 + … + αk-1λk-1fk-1 + αkλkfk = θ; (4)
Равенство (3) умножаем на λk и вычтем из (4).
α1( λ1 - λk )f1 + α1( λ2 - λk )f2 + … + α1( λk-1 - λk )fk-1 = θ.
По индуктивному предположению f1, …, fk-1 – линейно независимы .
0 = α1( λ1 - λk ) = α2( λ2 - λk ) = … = αk-1( λk-1 - λk ).
Т. к. λk ≠ λ; i = 1, …, k – 1, то α1 = … = αk-1 = 0.
αkfk = θ, т. к. fk ≠ θ, то αk = 0
Итак, α1 = … = αk-1 = 0 => f1, …, fk-1, fk – линейно независимы.
Билет 27. Критерий диагональности матрицы линейного оператора. Теорема о приведении к диагональному виду матрицы линейного оператора с простыми собственными значениями.
Опред.
15.
Квадратная матрица Anxn
имеет диагональный вид, если ∀i,
j
= 1, …, n:
i
≠ j,
aij
= 0 ( aij
= 0 ), т.е.
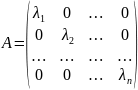
Теорема 11. ( Критерий диагональности матрицы линейного оператора в некотором базисе ).
Пусть
Vn
– n-мерное
линейное пространство, A
L(
Vn
), [e]
= ( e1,
… , en
)
– базис Vn,
Ae
– матрица оператора А
в [e].
Матрица Ae
линейного оператора в базисе [e]
диагональна т. и т. т., когда базис
состоит из собственных векторов
оператора A,
причём в этом случае
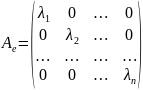
Aei = λiei i=1, …, n ( т.е. λi собственное значение соответствующее собственному вектору ei.)
Док-во:
Необходимость. Пусть
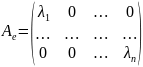
тогда, по определению матрицы линейного оператора, Ae1 = λ1e1, …, Aen = λnen, т. е. e1, …, en собственные вектора оператора A, отвечающие собственным значениям λ1, …, λn.
Достаточность. Пусть e1, …, en базис из собственных векторов оператора A. Тогда Aei = λiei. i = 1, …, n.
[e]: A→
Опред. Оператор называется диагонализируемым, если в пространстве Vn базис, в котором матрица оператора диагональна. Оператор диагонализируем в пространстве т. и т. т., когда в Vn базис из собственных векторов этого пространства.
Теорема 12. Пусть A L( Vn ). Если у оператора А λ1, λ2, …, λn - n различных собственных значений, то A – диагонализируемый оператор ( т. е. в Vn базис, в котором матрица оператора имеет диагональный вид ).
Док-во: Собственные значения λ1, …, λn соответствуют системе собственных векторов оператора A: e1, e2, …, en такая, что Aei = λ1e1, i = 1, …, n. Согласно теореме 10 (Если λ1, λ2, …, λk – различные собственные значения оператора A (т. е. λi ≠ λj, при i ≠ j, то собственные вектора f1, f2, … , fk, отвечающие данным собственным значениям являются линейно независимыми)) собственный вектор оператора A, отвечающий различным собственным значениям, линейно независим. Т.к. по условию собственных значений n и λi ≠ λj при i ≠ j,
то e1, … , en – линейно независим.
Т. к. dim Vn = n, то векторы e1, …, en образуют базис Vn.
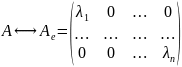
Определение
16.
Говорят, что квадратная матрица A
приводится к диагональному виду, если
она подобна диагональной матрице, т.
е. если
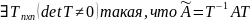 , где
, где
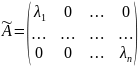 – диагональная матрица.
– диагональная матрица.
Следствие: Если матрица A имеет n различных корней, характеристического многочлена, то её можно привести к диагональному виду.
Билет 28. Билинейные формы в действительном линейном пространстве. Симметричные и кососимметричные линейные формы, представление билинейной формы через координаты векторов.
V – действительное линейное пространство.
Определение: Билинейной формой на линейном пространстве называется числовая функция F( x, y ) от 2-х элементов x, y V, линейная по каждому аргументу ( при фиксированном втором ). Т. е. x, y, z V и
1) F( x + z, y ) = F( x, y ) + F( z, y );
F( x, y ) = F( x, y );
2) F( x, y + z ) = F( x, y ) + F( x, z );
F( x, y ) = F( x, y ).
Примеры:
1) f и g – линейные формы на V.
F( x, y ) = f( x )g( y ) – билинейная форма.
2) V3 – линейное геометрическое пространство векторов x, y V3. :
F( x, y ) = ( x, y ) = |x|*|y|*cos - билинейная форма.
Определение: Билинейная форма F( x, y ) на V называется:
1) Симметричной, если x, y V: F( x, y ) = F( y, x )
2) Кососимметричной, если x, y V: F( x, y ) = -F( y, x ).
F( x, y ) – билинейная форма на n-мерном линейном пространстве Vn
[e] = ( e1, e2, …, en ) – базис Vn
x,
y Vn
:

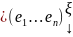
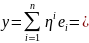 )
)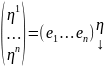
=
=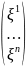 и
=
и
= ;
;
Билет 29. Преобразование матрицы билинейной
формы при изменении базиса.
Vn – n-мерное пространство;
F( x, y ) – билинейная форма на Vn. x, y ϵ Vn.
[e]
= ( e1,
… , en
)
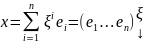
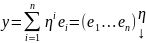
F(
x, y )
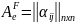
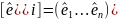 ;
;
 ;
;
 ;
;
[e]:
F( x, y )


Пусть S – матрица перехода от [e] к [e^]
(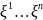 )
= S(
)
= S(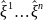 );
);
 =
S
=
S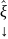 ;
;
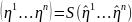 ;
;

 =
=
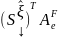 (
( )
=
)
=
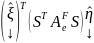
 =
=
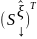 =
=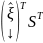 ;
;
В
силу единственности:
 =
=
Билет 30. Квадратичные формы в линейном пространстве, полярная билинейная форма. Приведение квадратичной формы к каноническому виду по методу Лагранжа.
Пусть V – действительное линейное пространство.
Определение 7. Пусть F(x, y) – симметричная билинейная форма на линейном пространстве V. Числовая функция q(x), полученная из F(x, y) путём замены y на x ( т. е. q(x) = F(x, x)) называется квадратичной формой на V. Билинейная форма F(x, y) называется полярной к квадратичной форме q(x).
Свойство квадратичной формы
Между квадратичными формами и симметричными билинейными формами на V взаимнооднозначное соответствие. F(x, y) q(x).
Определение
8. Матрицей
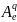 квадратичной формы q(x)
в базисе [e]
называется матрица полярной ей билинейной
формы F(x,y)
в базисе [e].
квадратичной формы q(x)
в базисе [e]
называется матрица полярной ей билинейной
формы F(x,y)
в базисе [e].
q(x)
=
 .
.
[e]
= ( e1,
… , en
);
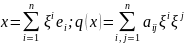 ;
;
 =
=
 ;
;
i,
j = 1, …, n.
 +
2
+
2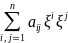
Определение
9. Говорят,
что в базисе
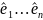 n
квадратичная форма имеет канонический
вид, если q(x)
= λ1(
1
)2
+ … + λn(
n
)2,
где
n
квадратичная форма имеет канонический
вид, если q(x)
= λ1(
1
)2
+ … + λn(
n
)2,
где
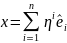 .
В этом случае базис [
.
В этом случае базис [ ]
называется каноническим.
]
называется каноническим.
Теорема
2. ( Метод Лагранжа ). Пусть
в некотором базисе квадратичная форма
F(
x,
y
) задаётся в виде:
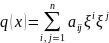 ;
(
=
,
;
(
=
,
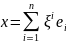 )
)
Тогда в Vn базис [ ] = ( ) в котором квадратичная форма имеет канонический вид: q( x ) = λ1( 1 )2 + λ2( 2 )2 + … + λn( n )2, где
Док-во:
Билет 31. Закон инерции квадратичных форм. Классификация квадратичных форм. Критерий Сильвестра положительной определённости квадратичных форм.
Теорема 3. ( Закон инерции ). Число положительных и отрицательных коэффициентов в нормальном виде квадратичной формы не зависит от базиса, в котором квадратичная форма приведена к нормальному виду. Т. е. [e^] = ( e^1, …, e^n ).
x = ni = 1^ie^i;
q( x ) = ( ^1 )2 + … + ( ^p^ )2 – ( ^p^+1 )2 -…- ( ^p^+q^ )2; p^ + q^ n.
[e~] = ( e~1, …, e~n ); x = ni = 1~ie~i;
q( x ) = ( ~1 )2 + … + ( ~p~ )2 - ( ~p~+1 )2 - … - ( ~p~+q~ )2;
p~ + q~ n; т. е. p^ = p~; q^ = q~; (Без док-ва).
Определение 11. Пусть в некотором каноническом базисе квадратичная форма q( x ) имеет вид:
q( x ) = ( 1 )2 + … + ( p )2 - ( p+1 )2 - … - ( p+q )2;
тогда число положительных коэффициентов в нормальном виде ( p ) называется положительным индексом инерции q( x ), а число отрицательных коэффициентов ( q ) – отрицательным индексом инерции.
p + q n.
Определение 12. Квадратичная форма q( x ), заданная на действительном линейном пространстве, называется:
1) Положительно определённой, если x V, x : q( x ) > 0;
2) Отрицательно определённой, если x V, x : q( x ) < 0;
3) Знакопеременной, если x, y V: q( x ) >0, q( y ) < 0;
4) Положительно полуопределённой, если x V: q( x ) 0 и y V, y : q( y ) = 0;
5) Отрицательно определённой, если x V: q( x ) 0 и y V, y : q( y ) = 0;
Теорема 4. Пусть квадратичная форма q( x ) задана на действительном конечномерном пространстве Vn, p и q – её положительный и отрицательный индексы инерции, тогда квадратичная форма:
1) положительно определена <=> p = n, q = 0;
2) отрицательно определена <=> p = 0, q = n;
3) знакопеременная <=> p > 0, q > 0;
4) положительно полуопределена <=> 0 < p < n, q = 0;
5) отрицательно полуопределенна <=> p = 0, 0 < q < n.
( Без док-ва ).
Vn; e1, … , en – произвольный базис; x = ni=1iei;
q( x ) – квадратичная форма.
Aiq – матрица q( x ) в [e]; q( x ) = ni, j = 1 aijij.
( a11 a12 … a1n )
Aiq = ( a21 a22 … a2n )
( ……………… )
( an1 an2 … ann )
Определение 13. Величины d1 = a11;
d22 = M( 1 2 ) = ( a11 a12 )
( 1 2 ) = ( a21 a22 );
dk = M( 1, …, k ) = | a11 a12 … a1k |
( 1, …, k ) = | ak1 ak2 … akk |, …,
dn = |Aeq| = | a11 … a1n |
| an1 … ann |
называются главными минорами матрицы Aeq.
Теорема 5 ( Критерий Сильвестра ).
1) Квадратичная форма q( x ) на Vn является положительно определённой т. и т. т., когда все её главные миноры положительны.
( Т. е. k = 1, …, n: dk > 0 ).
2) Квадратичная форма q( x ) на Vn является отрицательно определённой т. и т. т., когда знаки её главных миноров чередуются, причём d1 < 0.
( Т. е. k = 1, …, n: ( -1 )kdk > 0 ).
Пример: V2; n = 2; x = x1e1 + x2 e2;
q( x ) = Ax12 + 2Bx1x2 + Cx22;
( A B )
Aq = ( B C )
1) Положительно определена q( x ) > 0 <=> d1 = A > 0;
| A B |
d2 = | B C | = AC – B2 > 0.
2) Отрицательно определена q( x ) < 0 <=> d1 = A < 0;
| A B |
d2 = | B C | = AC * B2 > 0.
3) Знакопеременная | A B |
d2 = | B C | < 0;
4) В остальных случаях q( x ) полуопределена.
( Без док-ва ).
