14. Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при изменении базиса

V –линейное пространство [e]=(e₁…, e_n) – базис V

[ê]=(ê₁, …, ê_n) — базис V

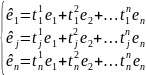ê_j=(e₁, …, e_n) j=1, .., n

T= = 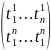(ê₁, ê₂, … ê_n)=(e₁, e₂, …, e_n) T

[ê]=[e]T T – матрица перехода

Теорема. Если V — n-мерное линейное пространство, то невырожденные

квадратные матрицы порядка n и только они могут являться матрицами

перехода от одного базиса к другому

Док-во: зафиксируем [e]=(e₁…, e_n) – базис V

Необх.: Пусть [ê]=(ê₁, …, ê_n) — другой базис V.По определению матрица перехода T от базиса [e] к базису [ê] состоит из столбцов координат вектора базиса [ê] в базисе [e] т.к. ê₁, …, ê_n – линейно независимы, то столбцы их координат линейно независимы и следовательно, если матрица не вырождена, т.е. если [ê]=[e]T, то det T ≠0.

Дост: Пусть det T≠0 (T- произвольная невыраженная матрица).Построим строку векторов (ê₁, ê₂, … ê_n)=(e₁, e₂, …, e_n) T.Покажем, что [ê] — базис T=llt_jⁱll_nⁿ , ê_k= 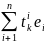, k=1, …, n, т.е. в k- ом столбце матрицы T расположен столбец координат ê_k в базисе [e] т.к. detT ≠0, то столбец T линейно независим по лемме 1 получаем, что вектор ê₁, …, ê_n – линейно независим, Т.к. dim V=n, то ê₁, …, ê_n – образуют базис, т.е. T[e]→ [ê]

Следствие. Если матрица T- матрица перехода от базиса [e] к базису [ê], то матрица перехода от [ê] к базису [e] будет матрица

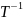
Док-во: (ê₁, ê₂, … ê_n)=(e₁, e₂, …, e_n) T. По теореме detT ≠0=> ∃

(ê₁, ê₂, … ê_n) =((e₁, e₂, …, e_n)T) =(e₁, e₂, …, e_n)T =(e₁, e₂, …, e_n), т.е.

(ê₁, ê₂, … ê_n) =(e₁, e₂, …, e_n), где –матрица перехода от [ê] к [e]

Преобразование координат вектора при изменении базиса.

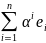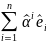x= =(e₁, …, e_n) x= =(ê₁, …, ê_n)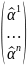

x=(e₁, …, e_n) =(ê₁, …, ê_n) =((e₁, …, e_n)T) =(e₁, …, e_n)[T ]=> = T =>

=> = T^-1 – формула преобразования координат

α ^k=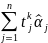

15. Определение линейного подпространства. Свойства линейного подпространства

Опред. Непустое подмножество L линейного пространства V называется линейным подпространством линейного пространства V, если:

1. ∀x, y ∈ L: x+y∈ L

2. ∀x ∈ L и ∀λ+y∈ ℝ: λx∈L

Св-ва линейного п/п

1. Линейное п/п L линейного пр-ва V само является линейным пространством относительно операции сложения и умножения числа, определенное в V.

Док-во. Т.к. L непустое, то∃x ∈ L.Т.к. L –лин п/п, то ∀λ∈ ℝ: λx∈L

1. λ=0 0*x= θ∈L

2. λx∈L:-x=(-1)x∈L=>λ=-1

Аксиомы 5-8 выполняются и в V, и в L

2. Любое линейное п/п n-мерного пространства конечномерно и его разность не превосходит n. иначе: если dim V=n, то dim L ≤ n

Док-во: Т.к. dim V=n, L<V, то ∀ n+1 элементы ∈ L –линейно зависимы=> L –конечномерно и dim L≤n

3) Линейное п/п L конечномерного пространства V совпадает со всем пространством тогда и только тогда, когда dim V=dim L

Док-во: а) L<V(все пр-во само линейное п/п)

dim L=dim V

б) Пусть dim V=n, L –линейное п/п V и dim L=n

Т.к. dim L=n, то в L ∃ базис (e₁, …, e_n).Поскольку L<V, то (e₁, …, e_n) ∈V dim V=n, то (e₁, …, e_n) – базис V =>∀x ∈V ∃α¹, …, α^n, что x= ∈L => L=V