Проекция вектора-момента силы относительно точки на ось, проходящую через эту точку, равна моменту силы относительно оси .

 

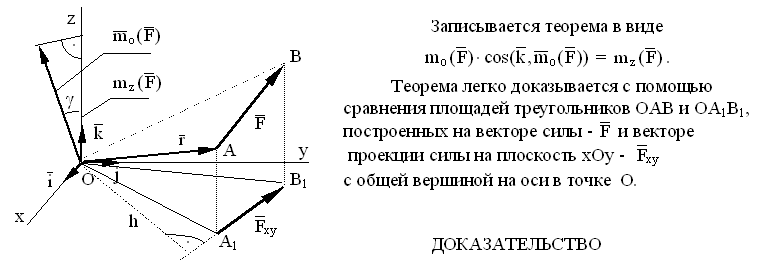
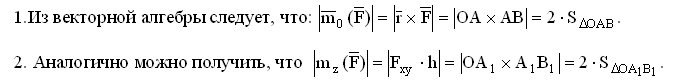
На основании этой теоремы из выражения  =   получают аналитические формулы  для 

                              определения моментов силы  относительно координатных осей.

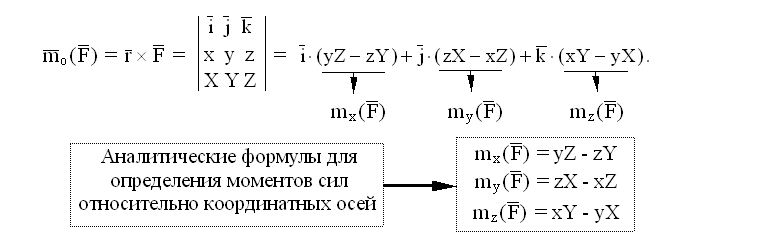
  Заучивать аналитические формулы на память нецелесообразно, а вот вывести их несколько раз для  себя, чтобы не забыть, как определяются проекции вектора,  являющегося произведением двух других векторов, стоит.     С векторными произведениями  в механике  придется встретиться еще не раз.

Системы параллельных сил

 

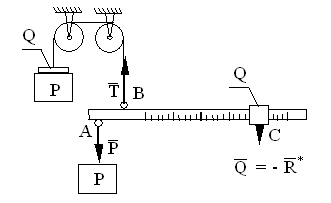
Рассмотрим сначала силы, направленные в одну сторону.  Эту систему сил можно привести к сходящейся, добавив к ней простейшую уравновешенную систему сил (так это сделано на плакате,  а затем привести к равнодействующей. Легко доказывается,  что линия  действия R* проходит от точек приложения сил на расстояниях обратно пропорциональных силам.  Можно привести и  иное доказательство.

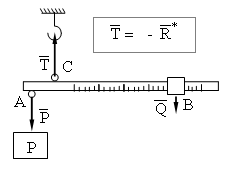
 Для  этого взвесим какой-либо груз на безмене - неравноплечих весах,  схема  которых приведена  на рисунке.

Взвешивание на таких весах осуществляется  перемещением постоянного по весу груза Q  по длинному плечу рычага весов до тех пор, пока рычаг при  равновесии  не  займет горизонтального положения.

Из условия равенства моментов сил  Р и Q

              (PAC = QBC)  относительно оси подвеса рычага - т. С   следует, что:

                  ;           ,

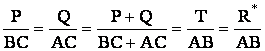где  k - константа для данных весов.  По длине плеча груза Q,  которое градуируется в единицах силы, и определяют вес взвешиваемого груза.     Ясно,  что  на  подвеску в т. С    со стороны рычага действует равнодействующая сил  Р и Q,  равная сумме  модулей  этих  сил.      Со стороны подвески на рычаг действует сила, равная равнодействующей, но направленная противоположно ей.  Эту силу принято называть  УРАВНОВЕШИВАЮЩЕЙ.

На этих же весах можно доказать,  что две неравные параллельные противоположно направленные силы также можно привести к равнодействующей.

  Для  доказательства точку подвеса рычага весов (обозначив  ее на рисунке  как точку приложения второй известной силы снова    буквой В)  сделаем подвижной, прикрепив ее к концу нити,  переброшенной через систему блоков и нагруженной на конце  грузом, равным сумме весов   Р и Q.

Для силы  Р  и  силы   T = P + Q    уравновешивающей в данном случае будет сила Q,    приложенная в точке С.         

                        А  уравновешивающая  равна  R*   и  противоположна ей.  

  Из равенства моментов сил  Р и Т    относительно т. С    –  ( PAC - T BC = 0)     получим:

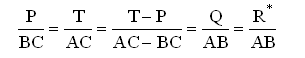
 то есть пропорцию, аналогичную полученной ранее.

         Однако есть и отличие. Из пропорции следует, что при  Т = Р  рычаг не может находиться в равновесии 

                                 и  что система сил      и   -   не может быть заменена одной силой.  

ТАКАЯ  СИСТЕМА  РАВНЫХ  ПО  МОДУЛЮ, ПАРАЛЛЕЛЬНЫХ  И  ПРОТИВОПОЛОЖНО  НАПРАВЛЕННЫХ 

СИЛ  НЕ  ИМЕЕТ  РАВНОДЕЙСТВУЮЩЕЙ   И  ВЫДЕЛЯЕТСЯ    КАК  ОСОБАЯ  СИСТЕМА  СИЛ  !!!

 Заканчивая рассуждения о приведении к  равнодействующей  двух параллельных сил, сделаем следующие выводы:                

Разговор об  этой  системе  сил пойдет  в  следующей комнате нашего здания, на двери которого висит

    табличка  “ПАРА СИЛ”     с дополнительным пояснением - определением.