Большие и сверхбольшие интегральные схемы

1. Что называется БИС и СБИС?

2. Что называется микропроцессором?

3. Охарактеризуйте основные параметры и показатели работы микропроцессоров.

4. Приведите структурную схему и поясните назначение отдельных блоков микропроцессора.

5. Изобразите структурную схему и поясните назначение отдельных блоков микро-ЭВМ.

6. Что называется внешним запоминающим устройством?

7. Что называется внутренним запоминающим устройством?

8. Что называется ОЗУ?

9. Что называется ПЗУ?

10. Что называется ППЗУ?

11. Что называется РПЗУ?

12. Изобразите структурную схему и поясните назначение блоков ОЗУ.

13. Изобразите структурную схему и поясните назначение блоков ПЗУ.

14. Изобразите схемы ячеек и поясните принцип работы элементов ПЗУ.

15. Изобразите схемы ячеек и поясните принцип работы элементов РПЗУ.

16. Изобразите структурную схему и поясните принцип действия РПЗУ с ультрафиолетовым стиранием.

17. Что называется ЦАП?

18. Поясните возможность реализации ЦАП на основе двоично-весовых резисторов.

19. Поясните возможность реализации ЦАП на основе резисторов R, R/2.

20. Что называется АЦП?

21. Изобразите структурную схему и поясните принцип действия АЦП.

6 Основы наноэлектроники

6.1 Физические основы наноэлектроники

Общие сведения

Наноэлектроника — электроника полупроводниковых структур с характерными размерами от 0,1 до 100 нм (1нм=10^-9м=10 ). Термин «нано» (от греческого «нанос»— карлик) был введен в информационные технологии в середине 70-х годов 20 века. Нанометр – величина порядка нескольких атомов, построенных в цепочку. Некоторые характерные объекты с такими размерами имеют вид в соответствии с рисунком 6.1.

Атом С

0,16нм

ДНК

2,5 нм

Молекулярная шестеренка

10нм-100нм

Одноэлектронный транзистор 300 нм

Красные

кровяные

тельца

8 мкм

Человеческий волос

50-100 мкм

Рисунок 6.1 – Наноразмерные объекты

В современных (2004 г.) процессорах фирмы Intel размеры отдельных элементов составляют уже менее 65 нм. К 2009 г. планируют освоить промышленный выпуск транзисторов с тройным затвором, длина которого будет 15 нм (32-нанометровый технологический процесс). В отличии от классических планарных транзисторов в трехзатворных транзисторах используют новую структуру, в которой затворы как бы «обернуты» вокруг трех сторон кремниевого канала. Подробнее трехзатворные транзисторы будут рассмотрены ниже.

Поскольку как научное направление «наноэлектроника» существует относительно недавно, то ее точного исчерпывающего определения пока не существует. Наноэлектроника составляет часть нанотехнологии – области науки и техники, описывающей процессы, происходящие в пространстве с линейными наноразмерами и позволяющей конструировать, изготовлять и использовать на практике наноразмерные объекты и системы различной природы: искусственные, созданные человеком, молекулярные, биологические, химические и физические.

В настоящее время в развитии нанотехнологий существует три основных взаимосвязанных направления:

• изготовление электронных схем, в том числе объемных (аналогичных нейросетям), с активными элементами, размеры которых сравнимы с размерами единичных молекул или атомов;

• непосредственное манипулирование атомами и молекулами, а также сборка из них всевозможных материалов с наперед заданными свойствами (при этом методы управления энергетической структурой вещества получили специальное название – «зонная инженерия»);

• разработка и изготовление наномашин, т.е. механизмов и роботов величиной с молекулу, способных на принципах самоорганизации воспроизводить себе подобных.

Техническая возможность использовать нанотехнологии на практике появилась впервые в 1981 после изобретения Г.Бинингом и Г Рорером сканирующего туннельного микроскопа, позволяющего структурно воздействовать на вещество на атомном уровне. В 1986 г. был создан атомно-силовой микроскоп, который в отличие от туннельного микроскопа, может осуществлять манипуляции не только с проводящими, а с любыми материалами. При помощи туннельного микроскопа стало возможным захватить отдельный атом и поместить его в нужное место, т.е. атомарно конструировать полупроводниковую наноструктуру или вещество с необходимым химическим составом и конфигурацией.

Теоретически (в некоторых прогнозах) считается, что нанотехнология позволит создавать практически любые изделия – от вычислительных машин сверхвысокой производительности (квантовых компьютеров) до искусственных органов человека.

Наноэлектроника является логическим развитием микроэлектроники по пути микроминиатюризации. Данное развитие происходило и происходит до сих пор в полном соответствии с законом Г.Мура (удвоении производительности ИМС каждые 18 месяцев, начиная с 1965 г., и каждые 24 месяца с 1975 г.). Наиболее характерные этапы этого развития показаны на рисунке 6.2.

Если темпы такой миниатюризации сохранятся до 2010г., то транзистор уменьшится до размеров вируса, его рабочая частота сравняется с частотой колебаний атомов в решетке кристалла, а число транзисторов в одной ИМС достигнет одного триллиона.

Современное развитие твердотельной нанотехнологии базируется на основе последних достижений физики твердого тела, квантовой электроники, физической химии и технологии полупроводниковой электроники. В наноэлементах используются уже не электроны, как частицы, переносящие электрический заряд, а их волновые функции. Начинают в полной мере проявляться квантовые эффекты, а физика проводимости определяется квантово-механической интерференцией электронных волн. На основе фундаментальных физических процессов в таких элементах в настоящее время разрабатывают квантовые устройства и системы, работающие на новых принципах, с широкими функциональными возможностями для микро-, опто- и наноэлектроники, средств связи, измерительной техники, информационных технологий нового поколения.

Транзисторов/см²

10 210³ 2,510⁵ 410⁶ ~410⁷

1см

1мкм

50нм

1нм

1950 1960 1970 1980 1990 2000 2010 2020

Г оды

Рисунок 6.2 – Характерные тенденции развития микро и наноэлектроники

В недалекой перспективе достижения наноэлектроники позволят: создать квантовый компьютер; значительно увеличить пропускную способность каналов связи, увеличить информационные емкости и качество систем отображения информации с одновременным снижением энергозатрат и т.д. В отдельных областях промышленности контроль изделий и материалов на уровне единичных атомов стал обыденным, например, наноконтроль матриц, используемых в производстве DVD-дисков.

Говорят даже, что тот, кто овладеет сегодня нанотехнологией – овладеет будущим. Только в США на исследования в области нанотехнологии в течение 2004-2007 гг. планируют выделить 2,36 млрд. долларов, что более чем вдвое превышает суммы, направленные на эти цели в предыдущие три года.

Россия по масштабам фундаментальных и прикладных исследований в области нанотехнологий пока отстает от ведущих стран мира. Вместе с тем в ряде институтов РАН проводят серьезные работы в этой сфере. Так, в ФТИ под руководством нобелевского лауреата Ж.Алферова осуществляют передовые разработки наногетероструктур, получившие международное признание.

Прежде чем перейти к современным достижениям наноэлектроники, кратко рассмотрим некоторые квантовые эффекты, лежащие в основе функционирования наноразмерных элементов.

Квантово-механические свойства электрона

В микроэлектронных приборах поведение электрона определяется как поведение элементарной частицы, которая имеет определенные массу и заряд, а также обладает вполне определенными импульсом и энергией. Такие частицы двигаются по траекториям, которые можно рассчитать с помощью уравнений Ньютона (например, как в телевизионном кинескопе). Точные пространственно - распределенные картины токов и электростатических полей в таких структурах вычисляют на основе систем уравнений в частных производных, подобных рассмотренной в разделе 1 ФСУ, описывающей процессы диффузии, дрейфа и генерации- рекомбинации для электронов и дырок.

В наноэлектронных приборах поведение электрона основывается совершенно на иных принципах. Главная особенность квантово-механического описания электронов состоит в том, что электрон, оставаясь частицей, подобен волне (принцип де Бройля). При этом его пространственные координаты и величину импульса невозможно определить с высокой точностью (соотношение неопределенностей Гейзенберга), т.е. невозможно предсказать направление, в котором будет двигаться электрон, если известно, что в данный момент он расположен в какой-либо области пространства. И что еще более важно: поведение электрона теряет детерминированный характер, т.е. если в некоторый момент времени частица находилась в ограниченной области пространства, то в будущем невозможно достоверно предсказать ее местонахождение. Можно говорить лишь о распределении частицы в пространстве, о вероятности обнаружить ее в заданном месте.

Величина, описывающая это распределение, получила название -функции или волновой функции. Она дает вероятностное статистическое описание отдельного электрона. Интенсивность этой функции, а точнее квадрат ее модуля определяет вероятность обнаружения частицы в той или иной области: вероятность обнаружения частицы в интервале X равна . Волновая функция есть основная характеристика наноэлементов. Она содержит в себе полную информацию об электронах и других частицах в отдельно взятых атоме или молекуле, а также в целом по всему кристаллу.

Найти волновую функцию той или иной квантовой системы можно на основе решения краевой задачи для уравнения Шредингера, которое в стационарном одномерном случае имеет вид:

, (6.1)

где m – масса электрона (равная 9,10910^-31 кг);

– приведенная постоянная Планка (равная 1,054588710^-34Джс);

U(x) – потенциальная энергия;

E_П – полная энергия электрона.

В приборах наноэлектроники волновая функция выполняет роль носителя информации. Такой подход в представлении информации, ее обработке, и хранении по сути сводится к контролируемой передислокации волновой функции в наноструктуре. Обработка информации в таких наноэлементах заключается в перестройке волновых функций электрона, которая в литературе обозначается специальным термином – «инженерией волновых функций». Эта перестройка должна соответствовать заданному логическому закону преобразования информации.

Один из простейших способов перестройки волновой функции заключается в передислокации максимума вероятности нахождения из одной части квантовой системы в другую. Эта передислокация осуществляется под действием внешнего напряжения через полевые связи.

В такой наноструктуре «вход» и «выход» элемента локализованы не в пространстве, а в определенных промежутках времени, когда существует определенный порог внешних воздействий, соответствующий состоянию “вход” или «выход». Переход от одного устойчивого состояния наноструктуры в другое происходит через возбужденные неустойчивые состояния предельно быстро.

Подавляющее большинство новых физических явлений в наноструктурах также вытекает из волновой природы частиц (электронов и т.д.). Прежде всего это относится к эффектам, связанным с размерным квантованием (квантовыми ограничениями), интерференцией и туннелированием через потенциальные барьеры.

Размерное квантование (квантовое ограничение)

Как известно (см. раздел 1), свободные электроны в твердом теле перемещаются по любому из трех пространственных направлений. При уменьшении размеров полупроводниковых приборов до микромасштабов это свойство электронов сохраняется.

В том случае, когда по одной или нескольким координатам размеры наноструктуры становятся сравнимы с длиной волны де Бройля для носителей зарядов, свойства электронов сильно изменяются: на его движение накладывается некоторое пространственное ограничение. Эффект, возникающий при лимитировании движения электронов физическими размерами области, в которой он находится, называется эффектом локализации. Ясно, что свободные электроны являются нелокализованными.

Простейшим примером квантовой структуры, в которой происходит локализация, служит тонкая полупроводниковая пленка. Другие геометрические примеры структур с локализацией имеют вид в соответствии с рисунком 6.3, а их размерное описание приведено в таблице 6.1.

Тонкая пленка — это простейшая квантовая яма. В квантовой яме электроны проводимости локализованы по наименьшему измерению и нелокализованы (делокализованы) в плоскости, перпендикулярной этому измерению. Говорят, что в такой системе электроны образуют двумерный электронный газ. Более подробно квантовые ямы, проволоки и точки будут рассмотрены ниже.

Объем Яма Проволока Точка

Рисунок 6.3 – Прямоугольные наноструктуры

Таблица 6.1 – Размерности локализации и делокализации в наноструктурах

Наноструктура	Размерности делокализации	Размерности локализации
Объемный проводник	3 (X,Y,Z)	0
Квантовая яма	2 (X,Z)	1(Y)
Квантовая проволока	1(Z)	2(X,Y)
Квантовая точка	0	3 (X,Y,Z)

Главная особенность таких наноструктур состоит в том, что энергетически электроны в них могут рассматриваться как электроны в потенциальной яме, т.е. в ограниченной области, отделенной от остального пространства потенциальными барьерами. Простейшей моделью, наглядно демонстрирующей основные характеристики такой потенциальной ямы, является прямоугольный колодец с очень крутыми стенками. Потенциальные ямы могут быть одномерными, двумерными и трехмерными.

Из курса физики хорошо известно, что энергия, которой могут обладать электроны в таких системах, квантуется, т.е. может принимать только определенный набор дискретных значений. Явление, состоящее в квантовании энергии электрона, находящегося в потенциальной яме, называется размерным квантованием или квантовым ограничением.

Как показывается в квантовой механике, уровни энергии одномерной прямоугольной потенциальной ямы шириной b с бесконечно высокими стенками задаются уравнением

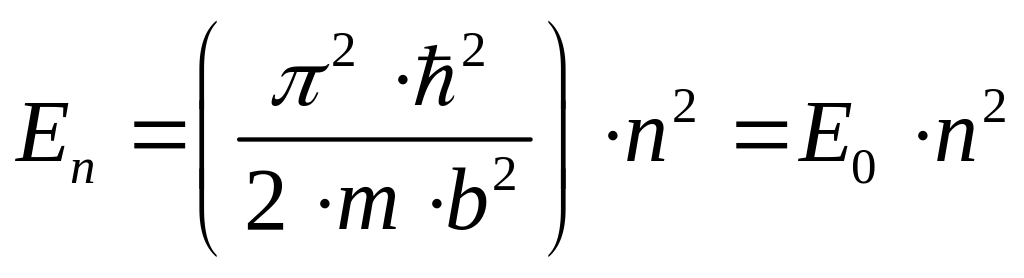, (6.2)

где n-квантовое число, принимающее значения 1,2,3,…;

Е₀- энергия основного состояния.

Величина минимальной энергии частицы, находящейся в потенциальной яме не может быть равна нулю. В типичных случаях ее величина изменяется от 0,02 эВ до 0,2 эВ.

Бесконечно глубокая яма имеет бесконечное число уровней с прогрессивно увеличивающемся расстоянием между ними при увеличении квантового числа n. Для конечной глубины ямы количество уровней конечно.

Волновые функции в потенциальной яме подобны стоячим волнам в натянутой струне

. (6.3)

Из формулы (6.3) следует, что длины волн -функций _n, описывающих электронные состояния с различными n, удовлетворяют условию:

, (6.4)

то есть в яме всегда укладывается целое число полуволн.

В других пространственных направлениях, где нет локализации электронов, длины волн для волновых функций могут быть произвольными, т.е. там сохраняются обычные объемные свойства электронов.

Теоретически можно показать, что для уверенного наблюдения квантовых размерных эффектов необходимо, чтобы толщина потенциальной ямы была маленькой, а носители в ней имели высокие подвижности (длина свободного пробега электрона должна значительно превосходить толщину ямы). В частности, для того, чтобы наблюдать этот эффект в наиболее распространенных полупроводниках при температурах вплоть до комнатной, нужно, чтобы b<10 нм, а подвижность превосходила несколько тысяч единиц [сантиметр в квадрате на вольт секунду]. Для тонких пленок существует еще одно условие — это высокое качество поверхности, необходимое для зеркального отражения носителей от границ пленки.

Размерное квантование приводит к тому, что энергетические диаграммы наноразмерных структур, а с ними и их электронные свойства, сильно отличаются от типичных объемных свойств материала, из которого они сделаны.

Интерференционные эффекты

Взаимодействие электронных волн в наноэлементах как между собой, так и с неоднородностями в них может сопровождаться интерференцией, аналогичной той, которая наблюдается для световых волн. Отличительная особенность такой интерференции от световой состоит в том, что в виду наличия у электронов заряда имеется дополнительная возможность управлять ими с помощью локального электростатического или электромагнитного поля и таким образом влиять на распространение электронных волн.

Одним из важных примеров интеренференционного эффекта в наноструктурах является магнитный эффект Ааронова-Бома. Схема эксперимента по наблюдению этого эффекта выполнена в соответствии с рисунком 6.4.

Пучок электронов, испускаемый из источника, в плоскости «а» расщепляется таким образом, чтобы он огибал магнитный поток с двух сторон. В плоскости «б» параллельные электронные пучки сливаются, и электронные волны интерферируют друг с другом. Относительная фаза электронов в двух пучках определяется магнитным потоком Ф, проходящим между двумя путями движения электронов. При изменении Ф будет меняться интерференционная картина, а следовательно, электронный ток и проводимость структуры.

Рисунок 6.4 – Схема эксперимента по наблюдению магнитного эффекта

Ааронова-Бома

При этом коэффициент прохождения D составит величину

. (6.5)

Тем самым электронный ток и проводимость структуры должны периодически осциллировать при изменении магнитного потока Ф.

Впервые эффект Ааронова-Бома наблюдался в цепи, состоящей из тонкого металлического золотого кольца с диаметром меньше одного микрона с двумя токоподводами. Размах осцилляций в такой конструкции не превышал 0,15 % от среднего значения сопротивления. В полупроводниковых интерферометрах на основе двумерного электронного газа размах осциляции составляет до 35 %.

Туннелирование

Способность квантовых частиц, в том числе и электронов, проникать через энергетическую преграду даже в случаях, когда их энергия ниже потенциального барьера, соответствующего данной преграде, называется туннелированием.

Уникальное для электронов явление туннелирования схематически имеет вид в соответствии с рисунком 6.5.

Рисунок 6.5 – Туннелирование электрона с энергией E через потенциальный

барьер высотой U, U > E

Будь электрон классической частицей, обладающей энергией E, он, встретив на своем пути преграду, требующую для преодоления большей энергии U, должен был бы отразиться от этой преграды. Однако, как волна, он хотя и с потерей энергии, но проходит через эту преграду. Соответствующая волновая функция, а через нее и вероятность туннелирования рассчитываются из уравнения Шредингера.

При этом вероятность туннелирования будет тем больше, чем геометрически тоньше барьер и меньше разница между энергией падающего электрона и высотой барьера.

Квантовое ограничение, проявляясь в наноразмерных структурах, накладывает специфический отпечаток и на туннелирование. Так, квантование энергетических состояний электронов в очень тонких, периодически расположенных в одном направлении потенциальных ямах (такие наноструктуры называются сверхрешетками) приводит к тому, что туннелирование через них приобретает резонансный характер, то есть туннельно просочиться через такую структуру могут лишь электроны с определенной энергией. Условная схема такого движения имеет вид в соответствии с рисунком 6.6.

Рисунок 6.6 – Резонасное туннелирование в сверхрешетках

Ширина потенциальных ям в таких системах составляет от единиц до десятков нанометров, что меньше длины свободного пробега электронов, но больше постоянной кристаллической решетки.

Подбором параметров сверхрешетки можно добиться того, что коэффициент прохождения D_П электрона через многобарьерную систему будет больше коэффициента прохождения через любой барьер этой системы. Данный эффект связан с интеренференцией волн де Бройля и так же может служить примером проявления размерных эффектов в наноструктурах.

Другим специфическим проявлением размерного квантования является одноэлектронное туннелирование в условиях кулоновской блокады. Это явление будет подробно рассмотрено ниже.

Квантовый эффект Холла

Еще одним важным для наноэлектроники размерным эффектом является квантовый эффект Холла, который был открыт сравнительно недавно – в 1980г. и за что в 1985 г. была присуждена Нобелевская премия по физике.

Квантовый эффект Холла возникает в квантовых ямах в сильном магнитном поле, перпендикулярном слою двумерных электронов. Суть эффекта состоит в том, что при описанных выше условиях и низких температурах существуют целые интервалы магнитных полей, в которых холловское сопротивление является константой (рисунок 6.7), значение которой не зависит ни от параметров образца, ни от условий эксперимента, а с поразительной точностью определяется комбинацией мировых констант

(6.6)

где – приведенная постоянная Планка,

q – заряд электрона, а N – целое число.

_XY

Ом

14000

12000

10000

8000

6000

4000

2000

Н

кГс

0

20

40

60

Рисунок 6.7 – Квантовый эффект Холла

Из формулы (6.6) вытекает, что с точностью, с которой можно измерить величину холловского сопротивления _XY можно определить величину . Иными словами квантовый эффект Холла представляет собой метод прецизионного измерения постоянной тонкой структуры . Это связано с тем, что значение скорости света с хорошо известно из других метрологических измерений с точностью, значительно большей, чем точность измерений в квантовом эффекте Холла или измерений q и в других случаях.

Для того, чтобы лучше понять квантовый эффект Холла его необходимо сравнить с обычным классическим эффектом Холла, известным из курса физики.

С точки зрения классической механики на электрон, движущийся со скоростью V в магнитном поле с напряженностью Н, действует сила Лоренца qНV/с, перпендикулярная к направлению V и заставляющая электрон вращаться по окружности радиусом r в соответствии с рисунком 6.8 (а).

Если к системе двумерных электронов помимо магнитного поля, направленного к плоскости рисунка, приложить еще и электрическое поле Е, лежащее в плоскости слоя (и направленное вдоль оси Х), то их движение будет носить своеобразный характер. В отличие от случая Н = 0, где электроны ускорялись бы вдоль поля Е в соответствии с рисунком 6.8 (б); при совместном влиянии двух полей движение происходит по траекториям, называемым циклоидами в соответствии с рисунком 6.8 (в).

а) под влиянием магнитного поля

б) под влиянием электрического поля

в) под влиянием магнитного электрического полей

Рисунок 6.8 – Движение электронов

Такое движение характеризуется отсутствием среднего смещения в направлении Е и средней скоростью V_H= сЕ/Н (при Е <<Н) в направлении, перпендикулярном обоим полям (холловское направление). Если концентрация двумерных электронов равна n, то полный ток в холловском направлении будет равен .В данном выражении l_X — длина образца вдоль оси х.

При этом холловское сопротивление R_Х, равное отношению холловского напряжения, возникающего в направлении, перпендикулярном протекающему току, к величине этого тока составит

. (6.7)

Таким образом, согласно классическим представлениям, холловское сопротивление R_X должно быть просто прямо пропорционально напряженности магнитного поля, т.е. обычной линейной зависимостью.