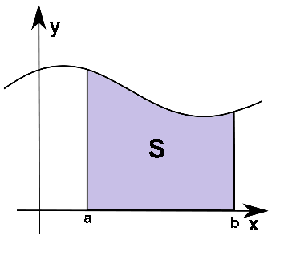
1. Определённый интеграл.

Определенный интеграл обозначается символом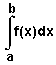 

Формула Ньютона Лейбница

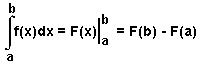
Свойства:

2.Несобственный интеграл первого рода.

Обозначение

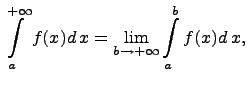
Определение Предположим, что функция   задана на бесконечном промежутке вида  и интегрируема на любом конечном отрезке   , где   . Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной:

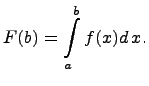
Если эта функция имеет предел при   , то число   называется значением несобственного интеграла первого рода:

а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения.

Критерий Коши. Если функция   интегрируема на отрезке  > , то для сходимости несобственного интеграла 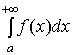  необходимо и достаточно, чтобы для любого сколь угодно малого положительного числа  >0 существовало число   такое, что для любых двух чисел  >  и  > , выполнялось неравенство

<

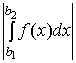3.Несобственный интеграл второго рода.

Обозначение

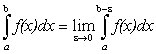
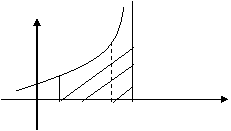
Пусть на полуинтервале   задана функция   , интегрируемая на любом отрезке, принадлежащем данному интервалу, однако не интегрируемая на отрезке   . В точке   эта функция может быть вовсе не определена и стремиться к   , либо вовсе не иметь никакого предела. Рассмотрим функцию

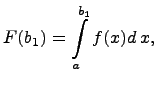
она определена при   . Эта функция может иметь предел при  (левосторонний предел). Этот предел будем называть значением интеграла от   по всему полуинтервалу   и обозначать в точности:

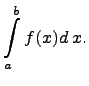
Определение. Пусть функция   удовлетворяет указанным выше условиям на   . Несобственным интегралом второго рода назовём определенный интеграл

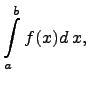
значение которого равняется левостороннему пределу

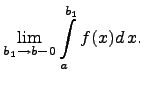
Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения.

4.Двойной интеграл.

Двойной интеграл в декартовых координатах. Пусть функция   определена и непрерывна в замкнутой ограниченной области D плоскости 0xy.

Разобьём область D произвольным образом на элементарные ячейки  , в каждой из которых зафиксируем точку . Составим сумму  , называемую интегральной, которая соответствует данному разбиению D на части и данному выбору точек  .

Если существует предел последовательности интегральных сумм   при  –диаметр ячеек   и этот предел не зависит ни от способа разбиения области D на элементарные ячейки, ни от выбора точек  , то он называется двойным интегралом от функции f(x,y) по области D и обозначается  .

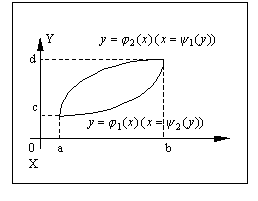
Вычисление двойного интеграла сводится к вычислению двукратных (повторных) интегралов. Пусть область D ограничена кривыми  ,  ,  ,  , причем  , а функции   непрерывны на отрезке  . Прямая, параллельная оси 0y, пересекает границу области D не более чем в двух точках. Такую область D называют простой и правильной в направлении оси 0y. Тогда 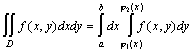 , причём сначала вычисляется внутренний интеграл по переменной y, а полученный результат интегрируем по x.

 Рис. 7

Если на отрезке   верхняя или нижняя граница области D задаются несколькими аналитическими выражениями, то область D следует разбить на количество областей, равное числу аналитических выражений верхней (или нижней) границы области (рис. 8), причём двойной интеграл по области D в этом случае равен сумме интегралов по полученным областям.

 Рис. 8

В том случае, когда область D ограничена кривыми  ,  , непрерывными на  , прямыми   и  , область D является простой и правильной в направлении оси 0x. Двойной интеграл по такой области вычисляют по формуле:  .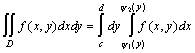

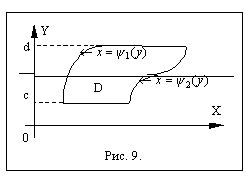
 Рис. 9

Если область D правильна в направлении обеих координатных осей, то двойной интеграл по такой области можно вычислять в любом порядке, то есть  .

 Двойной интеграл в полярных координатах. Пусть область D ограничена линией   и лучами   и  , где   и   – полярные координаты точки на плоскости, связанные с её декартовыми координатами x и y соотношениями  ,  . В этом случае    .

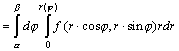Замечание. Если область D в декартовых координатах задаётся уравнением, содержащим бином x²+y², например, x²+y²=R², x²+y²=x,

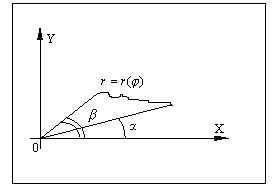
 Рис. 11

 x²+y²=x²-y² и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.