Билет 4.1

Лингвистические модели представления знаний в искусственном интеллекте

Лингвистическая переменная - переменная, значения которой может быть не только число, но и слова и словосочетания естественного языка.

Лингвистической переменной называется пятерка LV = (L, T, U, G, M),

L – название лингвистической переменной,

T – ее терм-множество (совокупность лингвистических значений),

U – универсальное множество числовых значений, i

G – множество синтаксических правил (грамматика), предназначенное для

образования составных термов из простых,

M – множество семантических правил, ставящих в соответствие каждому терму из T нечеткое множество в U.

Расширенная лингвистическая переменная есть набор

LVex = (L, T, U, G, M, RT, RU, D, H), где RT и RU – отношения на T и U соответственно, D – множество операций грануляции, H – множество преобразований универсума.

Билет 4.2

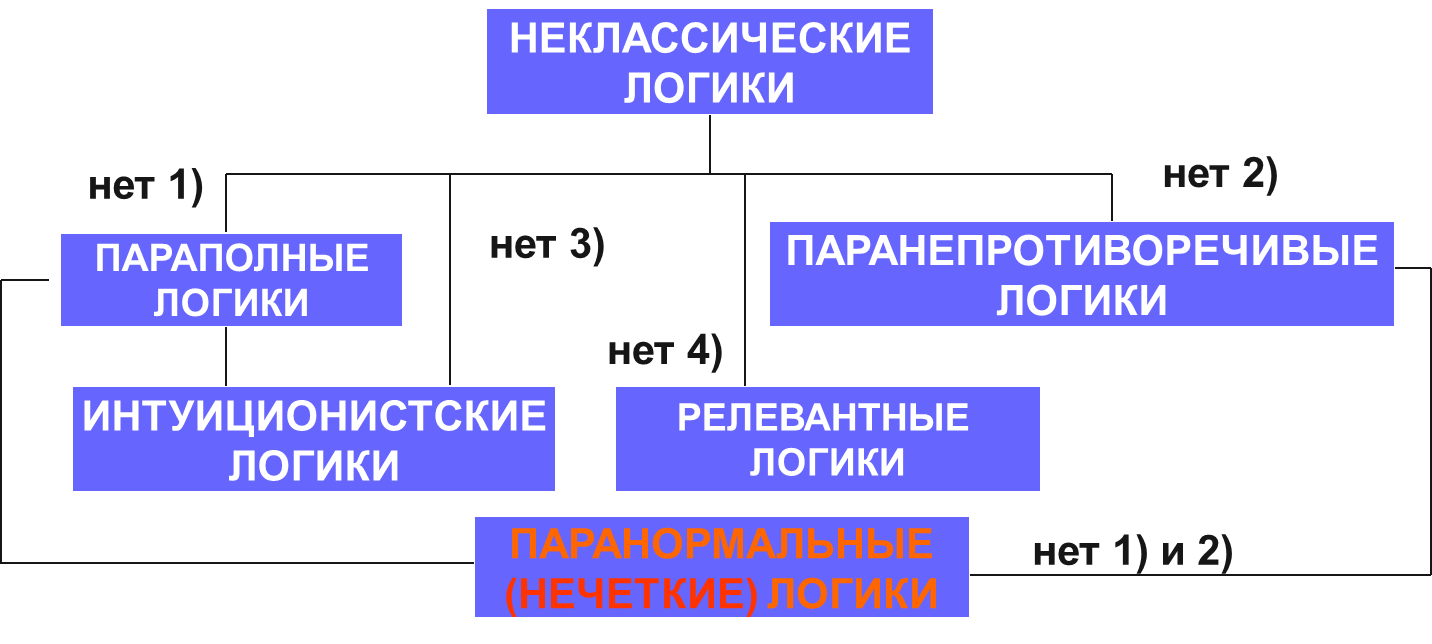
Основные законы классической логики и логической семантики. Их критика школой интуиционизма и российским логиком Васильевым. «Американский план» построения неклассических семантик и варианты его реализации.

Интуиционизм — система философских и математических идей и методов, связанных с пониманием математики как совокупности «интуитивно убедительных» умственных построений. С точки зрения интуиционизма, основным критерием истинности математического суждения является интуитивная убедительность возможности проведения мысленного эксперимента, связываемого с этим суждением. Поэтому в интуиционистской математике отвергается теоретико-множественный подход к определению математических понятий, а также некоторые способы рассуждения, принятые в классической логике.

1. закон тождества p=p;

2. закон полноты (исключенного третьего) p  p;

3. закон непротиворечивости  (p   p);

4. закон отрицания отрицания (закон инволютивности) ( p)= p;

5. закон материальной импликации (из лжи следует все что угодно)

Законы логической семантики

1. T(p) or F(p) Принцип бивалентности

2. not {T,F} Принцип однозначности

3. Т(p)+T(p) = 1 Принцип дополнительности

4. T( p) = – T(p) Принцип симметрии

Тезисы Васильева

1. Классическая логика не является универсальной и единственной, как когда-то Эвклидова геометрия

2. Логика – эмпирическая наука, то есть она зависит от свойств окружающей реальности или наших ощущений

3. Логический «Плюрализм» следует из 2

4. Закон исключенного четвертого (необходим, возможен, невозможен)

5. Воображаемая логика позволяет нам глубже проникнуть в природу нашей логики, разделить в ней эмпирические и неэмпирические элементы. Все неэмпирические элементы и отношения в логике составляют металогику.

6. Металогика есть учение о мышлении, не связанное с опытом.

Внутренняя логика – логика событий vs Внешняя логика – логика утверждений.

Билет 5.1

Наглядные модели представления знаний в искусственном интеллекте. Семантические сети. Сценарии. Когнитивные карты. Ментальные карты.

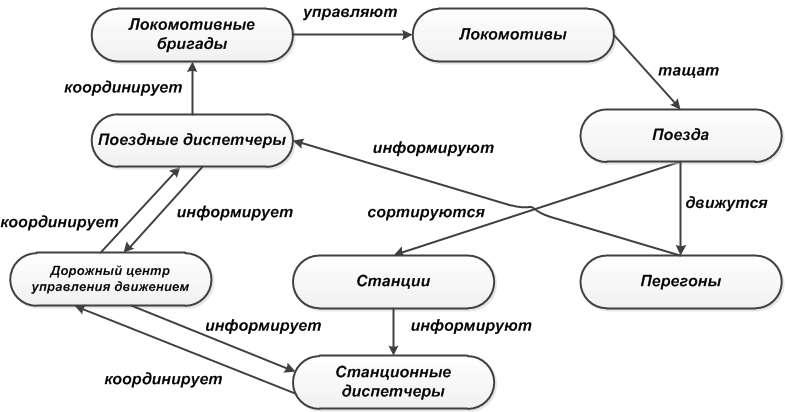
Семантическая сеть – это граф (мультиграф), вершинам которого поставлены в соответствие некоторые понятия (суждения), а дугам – связи (отношения) между этими понятиями (суждениями). SN = C, R

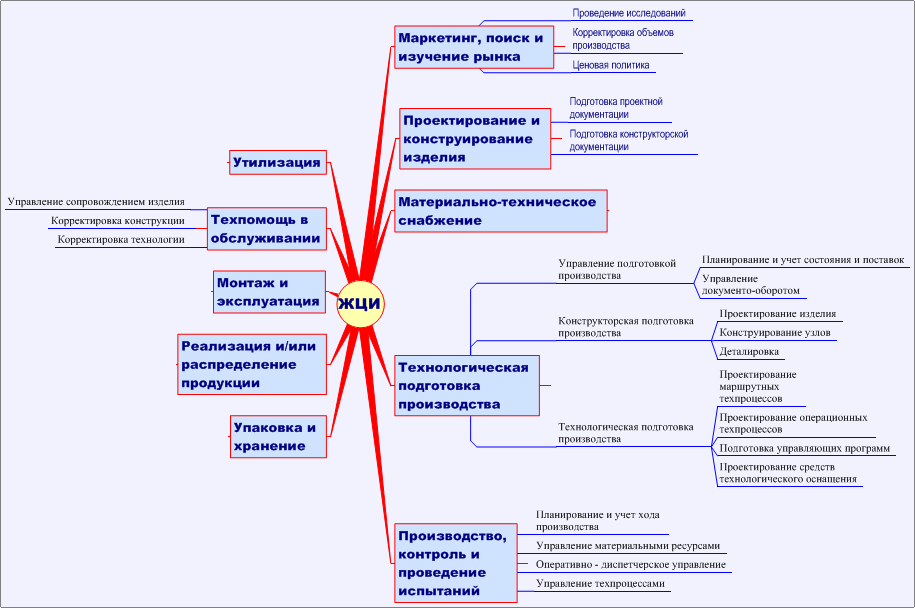
Основная идея ментальных карт (Mind Maps) заключается в поддержке правополушарных механизмов мышления путем преобразования фрагментов текстового (последовательного) изложения в сетевую (наглядно-образную) форму. Ментальная карта имеет следующие отличительные черты:

• Ее структура имеет форму куста

• Объект изучения сфокусирован в центре изображения (фокус внимания)

• Основные темы, связанные с объектом изучения, расходятся от центра в виде ветвей, которые поясняются ключевыми словами

• Вторичные идеи также ветвятся

• Ветви формируют связную узловую структуру

Когнитивная карта представляет собой знаковый граф:

СM = V, A, F, где: V – множество вершин (понятий),

A – множество дуг (связей между понятиями);

F = {+, –} – множество знаков дуг (типов связей между концептами).

Здесь, знак + выражает положительную связь, а через – обозначается отрицательная связь. В случае положительной связи усиление понятия-причины (фактора) приводит к усилению понятия-следствия: X Y, а при отрицательной связи усиление понятия-причины приводит к ослаблению понятия-следствия: X  Y

Фреймом называется минимальная структура для представления знаний в стереотипной ситуации.

FR = {N, <gi vi>}, где N – имя фрейма, gi – имя слота, vi – значение слота.

Фреймовые модели широко используются в различных областях. Например, они могут успешно применяться для представления заявок (заказов, предложений и поставок) в электронной коммерции. Приведем пример фрейма-прототипа для заказа в Интернет-магазине.

Заказ ={<ID>, <Потребитель, …>, <Адрес,…>, <Телефон, …>, <Товар, …>}.

Соответствующий фрейм-экземпляр может иметь вид:

Заказ = {<1283>, <ФИО, Иванов А.Б.>, <Адрес, Москва ул. Садовая д.3>, <Тел., +7-095-123-45-67>, <Товар, Велосипед Univega HT 510>}