[Править]Общие наблюдаемые переменные, которые подчиняются принципу неопределённости

Предыдущие математические результаты показывают, как найти соотношения неопределённостей между физическими переменными, а именно, определить значения пар переменных   и  , коммутатор которых имеет определённые аналитические свойства.

• самое известное отношение неопределённости — между координатой и импульсом частицы в пространстве:

• отношение неопределённости между двумя ортогональными компонентами оператора полного углового момента частицы:

где       различны и   обозначает угловой момент вдоль оси  .

• следующее отношение неопределённости между энергией и временем часто представляется в учебниках физики, хотя его интерпретация требует осторожности, так как не существует оператора, представляющего время:

• Следует подчеркнуть, что для выполнения условий теоремы, необходимо, чтобы оба самосопряженных оператора были определены на одном и том же множестве функций. Примером пары операторов, для которых это условие нарушается, может служить оператор проекции углового момента 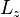  и оператор азимутального угла 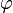 . Первый из них является самосопряженным только на множестве 2π-периодичных функций, в то время как оператор  , очевидно, выводит из этого множества. Для решения возникшей проблемы можно вместо   взять 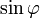 , что приведет к следующей форме принципа неопределенности^{[** 1]}:

.

Однако, при   условие периодичности несущественно и принцип неопределенности принимает привычный вид:

.

Билет 3.2

Определения и примеры неаддитивных мер. Меры возможности и необходимости. Их сопоставление с вероятностной мерой. Что такое нечеткий интеграл?

Пусть А и В – некоторые события, а Х – полное множество событий.

Мерой называется функция множества m: 2^X  R⁺, R⁺=[0,), которая удовлетворяет следующим условиям:

1. А2^X, АX  m (A) 0;

2. m() = 0;

3. А, В 2^X, m (A  B) = m (А) + m (В) – m (A  B).

Мерой Сугено называется функция множества

1. g: 2^X  [0,1], для которой выполняются следующие условия

2. g() = 0, g(Х) ≤ 1 (ограниченность)

3. А,В2^X, АВ  g(A)  g(B) (монотонность)

4. А,В2^X, АВ=  g(AB) = g(А)+g(В) + (g(А)+g(В)) (-правило) 1    .

5. А_n2^X, n=1,2,… если А₁  А₂ …, или А₁ А₂  …, то lim_n→ g(А_n) = g (lim _n А_n) (непрерывность)

В общем случае -правило записывается в виде

g_ (А_i ) =  g(А_i) +  П g(А_i), 1    .

Это правило получается из уравнения +1 = П(1+ _i). В результате при 0 получаем семейство субаддитивных мер:

 А, В 2^X, g_(A  B)  g_(А) + g_(B),

а при –10 – семейство супераддитивных (синергетических) мер

 А, В 2^X, g_ (A B)  g_(А) + g_(B).

При =0 мера Сугено превращается в обычную аддитивную (вероятностную) меру.

Мера возможности

П(pq) = max{П(p),П(q)} можно интерпретировать следующим образом: истинность дизъюнкции двух суждений определяется возможностью появления хотя бы одного из них.

Мера необходимости N (pq) = min {N(p),N(q)}

П (А)  P (A)  N (А)

P (A)+P (A) = 1

П (A) + П (A)  1, А2^X,

N (A) + N (A)  1, А2^X

nП (A) =1П (А), А2^X (Невозможность)

nN (A) =1N (А), А2^X (Случайность)

Кроме того, из П(А)  1 следует N (А) = 0 (неполная возможность события А приводит к абсолютной неуверенности), а из N(А)0 вытекает П(А)=1 (наличие некоторой уверенности в А означает его абсолютную возможность).

Нечеткий интеграл от h(x)

X -> [0,1]

A  X

∫h(x)*g = sup (A and g(a and H_a))

H_a = { x | h(x) >= a}