Билет 21.1

Логические модели знаний. Продукционные системы. Неклассические логики. Интуиционистские логики: определение и примеры (2.2 и 1.1).

В интуиционистских логиках нет закона исключенного третьего и слабое отрицание(n(n(p)) >P)

Логика Гейтинга

LM _H3 = {1, 0.5, 0}, {, , }, {1}

0.5 – «половинчатость» (не истинное и не ложное)

и

	1	0.5	0
1	1	0.5	0
0.5	0.5	0.5	0
0	0	0	0

или

	1	0.5	0
1	1	1	1
0.5	1	0.5	0.5
0	1	0.5	0

Продукционные правила подразумевают выполнение некоторого действия B в случае выполнения условия A. Данная модель хорошо выражает эвристические знания, циркулирующие в организационных сетях.

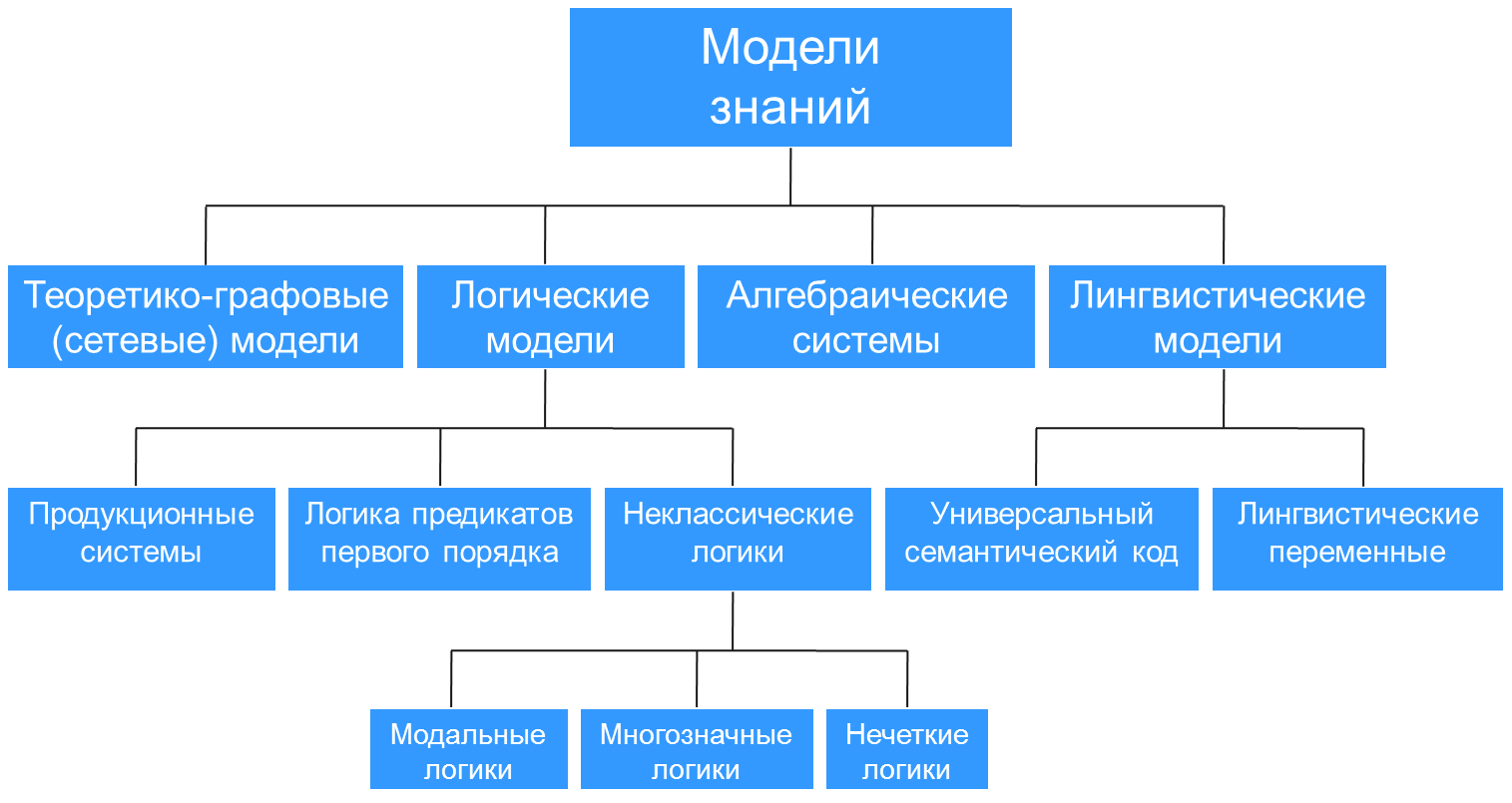
Билет 21.2

Классификация отношений. Связь между понятием разбиения и отношением эквивалентности. (См. 2.1).

Общие отношения для различных онтологий:

1. генеративные отношения «есть некоторый» (is_a);

2. таксономические отношения («класс-подкласс», «класс-экземпляр);

3. родо-видовые отношения;

4. партономические (или мереологические) отношения («часть–целое»);

5. отношения наследования или генеалогические связи («предок-потомок»).

Билет 22.1---

Основные интерпретации понятия информации. Формула Хартли. Формула Шеннона (16.1).

Виды информации.

Определение Информации

1. Сведения, которые расширяют понимания объекта

2. Сведения об окружающем мире и протекающих в них процесах

3. Абстрактное понятие, имеющие множество значений в зависимости от контекста

4. Сведения, данные, сообщения независимо от формы их представления

Виды информации:

1. графическая

2. текстовая

3. звуковая

4. видео

5. числовая

Формула Хартли

I=log2(N)=nlog2(m)

n – количество символов

m – мощность алфавита

N = m­ⁿ

Билет 22.1

Понятие онтологии. Виды онтологий. Модели онтологий. Для чего служат онтологии? Что такое метаонтологии? Примеры онтологий верхнего уровня. Как соотносятся онтологии с логиками?

См. 19.2

Билет 22.2

Алгебраические модели знаний. Алгебраические системы и их частные случаи. Логические матрицы. Нечеткие алгебраические системы.

См. 16.2 и 15.1.