Билет 18.1

Что такое универсальная логика? Приведите примеры основных алгебраических конструкций универсальной логики?

Универсальная логика – это не новая логика, а скорее попытка построить общую теорию логик, рассматриваемых как математические (в частности, алгебраические, геометрические, топологические) структуры.

Причина возникновения: реакция на логический плюрализм, появление сотен новых логик в последнее время, что влечет за собой потребность их систематизации и упорядочения.

Главный инициатор: Ж.-И. Безье (универсальная логика играет роль, аналогичную роли универсальной алгебры при изучении различных алгебраических структур)

Прародители: А. Тарский, А. Линденбаум, С. Яськовский.

Примеры основных понятий универсальной логики: логическая система, логическая операция, логическое следование, логическая матрица, многозначные логики

Под логикой (по Р.Вуйцицкому) понимается пара  = X, Cn, где X – множество логических формул, а Сn – оператор присоединения следствий, который удовлетворяет условиям: монотонности, рефлексивности, идемпотентности, структурности.

Билет 18.2

Треугольные нормы и конормы: формальные определения и примеры. Взаимосвязи между треугольными нормами и конормами.

См. 1.2. См. 15.1.

Треугольной нормой называется бинарная операция

удовлетворяющая четырем аксиомам:

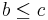
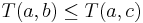•      и 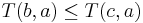  (монотонность);

• T(T(a,b),c) = T(a,T(b,c)) (ассоциативность);

• T(a,b) = T(b,a) (коммутативность);

• T(a,1) = T(1,a) = a (граничное условие).

Треугольной конормой называется бинарная операция

удовлетворяющая четырем аксиомам:

•      и 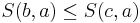  (монотонность);

• S(S(a,b),c) = S(a,S(b,c)) (ассоциативность);

• S(a,b) = S(b,a) (коммутативность);

• S(a,0) = S(0,a) = a (граничное условие).

Треугольная норма T и треугольная конорма S называются дополнительными бинарными операциями, если

T(a,b) + S(1 − a,1 − b) = 1

для  .

Наибольшей популярностью в теории Заде пользуются три пары дополнительных треугольных норм и конорм.

1) Пересечение и объединение по Заде:

T_Z(a,b) = min{a,b}, S_Z(a,b) = max{a,b}.

2) Пересечение и объединение по Лукасевичу:

.

3) Вероятностное пересечение и объединение:

Часто используемые в теории Заде дополнительные бинарные операции треугольной нормы и конормы собраны в таблице нечётких сет-операций.

Билет 19.1

Семантика Данна-Белнапа. Логика вопросов и ответов. Ее сопоставление с логикой Решера (15.2). Переход от логики Белнапа к бирешетке.

Основная идея семантики Дж.Данна заключается в отказе от принципа однозначности с допущением истиннозначных провалов I = { } = «ни истина, ни ложь» и пресыщенных оценок истинности B = {T, F} = «и истина, и ложь».

В первом случае оценки истинности и ложности понимают как частичные, а во втором – как составные, амбивалентные.

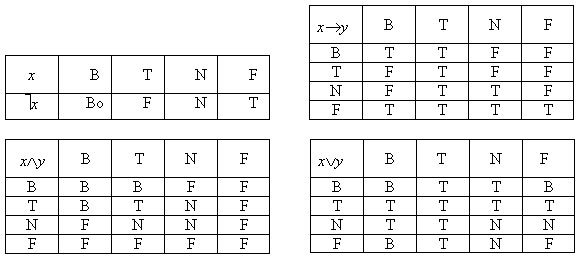
В целом, речь идет о переходе от обычного множества значений истинности V (например, V₂ = 2 = {T, F}) к множеству всех подмножеств 2^V, задающему мультиоценку истинности (например, 2^V2= 4={T, B, I, F})

LM B₄ = {T, B, N, F}, {, ,,}, {T}