Билет 13.2

Бесконечнозначная логика Геделя.

Смотри 1.2.

H₃  G_ Бесконечнозначная логика Геделя G_

LM_G3 =  [0,1], {, , }, {1}

Обобщение логики Геделя

LM_HL*=  [0,1], {1}, n*_H, I*_H,

1*. Семейство параметрических отрицаний n*_H(x) = [(1-x) / (1+x)]^k

2*. Семейство параметрических импликаций

I*_H(x,y) = 1, если x  y

(k+1)y/(k+x), если x  y

При k n*_H(x)  1, если x =0 (отрицание Геделя)

0, Если X 0

I*h(X,y)  1, если X y

y, если x y (импликация Геделя)

Билет 14.1

Наглядные модели представления знаний. Семантические сети. Когнитивные карты. Ментальные карты.

Смотри 5.1.

Билет 14.2

В чем заключается сходство и различие между теорией вероятности и теорией нечетких множеств? Что такое энтропия нечеткого множества?

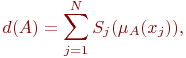
Где S — функция Шеннона S(y) = -y ln(y) – (1 - y) ln(1-y)

h₀() =  (x_i) (1- (x_i)).

h_SH() =  [(x_i) ln (x_i) +(1- (x_i)) ln (1-(x_i))].

В общем случае энтропию можно определить через отношение предпорядка _n как функцию h() = k S {T((x), n((x))}, xX, где T и S – треугольная норма и конорма соответственно, n – операция отрицания, а k – константа (коэффициент нормализации).

Билет 15.1

Нечеткие множества и основные операции над ними. Понятие множества уровня нечеткого множества и его практическое использование. Нечеткие алгебры и их свойства.

FAS =  F(X), R,  , где F(X) = {A A: X  L}, R = {r r: XX  L},

 = {^j_j}, _ст= {, , ', CON, DIL}

Частные случаи FAS

1. Вполне нечеткое множество [Ponasse,1984] - интегрированная модель, выражающая представления о принадлежности и неразличимости элементов множества А =  X, ,  , где : X  [0,1], : X  X  [0,1].

2. Нечеткая логическая матрица FLM= F(V), ,D, где F(V) = [0, 1]^V, D F(V).

Пусть L – решетка с наименьшим элементом 0 и наибольшим элементом 1.

Бинарная операция

T: L  L L S: L  L  L,

называется треугольной полунормой, треугольной полуконормой, если удовлетворяются следующие условия:

• ограниченность

1. T(0, 0) =0, T(x, 1) = T(1, x) = x, 1) S (1, 1) = 1, S(x, 0) = S(0, х) = x,

 x L;

• монотонность

2) x u, y v  T(x,y)  T (u,v), 2) x  u, y  v  S(x, y)  S (u, v),

 x, y, u, v L.

Пусть L – решетка с наименьшим элементом 0 и наибольшим элементом 1.

Бинарная операция

T: L  L L S: L  L  L,

называется

треугольной нормой, треугольной конормой,

если удовлетворяются следующие условия:

• ограниченность

1) T(0, 0) =0, T(x, 1) = T(1, x) = x, 1) S (1, 1) = 1, S(x, 0) = S(0, х) = x,

 x L;

• монотонность

2) x u, y v  T(x,y)  T (u,v), 2) x  u, y  v  S(x, y)  S (u, v),

 x, y, u, v L;

• коммутативность

3) T(x, y) = T(y, x), 3) S(x, y) = S (y, x),

x, y  L;

• ассоциативность

4) T(T(x, y), z) = T(x, T (y, z)), 4) S(S(x, y), z) = S(x, S (y, z)),

x, y, z L

Обобщения t-норм и t-конорм – унинормы U.

Пусть L – решетка с наименьшим элементом 0 и наибольшим элементом 1.

Бинарная операция U: L  L L называется унинормой, если выполняются следующие условия:

• наличие нейтрального элемента

e L, такого, что U (x, e) = U (e, x) = x,  x L;

• монотонность

x u, y v  U (x,y)  U (u,v),  x, y, u, v  L;

• коммутативность

U (x, y) = U (y, x), x, y  L;

• ассоциативность

U (U (x, y), z) = U (x, U (y, z)), x, y, z  L .