Билет 10.1

В чем заключается концепция плюрализма операций в нечеткой логике? Способы задания основных логических операций в многозначных и нечетких логиках. Что такое функционально-аксиоматическое определение операции? Приведите примеры.

Основоположники: Н.А. Васильев, Я. Лукасевич.

Истоки: аналогия с появлением неэвклидовых геометрий

Основной тезис: прикладная логика носит эмпирический характер , будучи сильно зависимой от множества онтологических и гносеологических факторов. Отсюда следует заключение о необходимости сосуществования множества различных логик (и семантик)

Способы задания см. 2.2.

Примеры функционально аксиоматического

Отрицание есть унарная операция n: [0,1][0,1], удовлетворяющая аксиомам:

1. ограниченности: n(0) = 1, n(1) = 0

2. антитонности: x  y  n(x)  n(y), x,y[0,1].

Операция отрицания, которая помимо условий

а) и б) удовлетворяет также условию

в) инволютивности n(n(x)) = x, x[0,1], называется инволюцией.

Билет 10.2

Что такое аргументация? Чем аргументация отличается от логического вывода? Логики аргументации Финна: семантики, операции, приложения.

Аргумент – логическая посылка, используемая отдельно или в совокупности с другими с целью доказательства истинности определенного суждения – тезиса.

Аргументация

1. Доказательная – установление истинности тезиса, являющегося достоверным суждением с использованием логических формул, с помощью аргументов, истинность которых установлена заранее. Форма аргументации – дедукция (от общего к частному).

2. Недоказательная

   1. Истинность аргументов не доказана (индукция).

   2. истинность аргументов установлена заранее, форма – индукция, аналогия.

   3. аргументы правдоподобны. Форма индукция, аналогия.

Логический вывод

Аргумент – суждение, посредством которого обосновывается истинность другого суждения.

Вывод – процесс рассуждения, в котором осуществляется переход от одних суждений к другим.

Отличие – аргументация, обоснование истинности, вывод – переход от одного суждения к другим.

Логика Финна LM=<{+1, -1, 0, t}, {not, imp}, {+1, -1}>

g+ доводы за

g- доводы против

если нет обоих, то неопределенность (т), если есть обе, то противоречие(0).

Билет 11.1

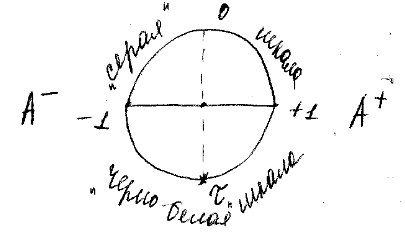
Чем измерение в науке отличается от оценивания? Что такое оппозиционные (биполярные) шкалы? «Серые» и «черно-белые» шкалы. Модель представления информации (оценок) на полярных шкалах.

СИСТЕМА ОППОЗИЦИОННЫХ ШКАЛ – ОБЪЕКТИВНАЯ ОСНОВА ПОСТРОЕНИЯ ОБРАЗА МИРА (ПО А.Н.Леонтьеву)

ОЦЕНИВАНИЕ НА ПОЛЯРНЫХ ШКАЛАХ – ВАЖНЕЙШИЙ СПОСОБ ФОРМИРОВАНИЯ ЧЕЛОВЕЧЕСКИХ ЗНАНИЙ

В мышлении человека порядок создается из хаоса путем формирования

системы оппозиционных (полярных) шкал и различения некоторых объектов

с помощью набора оценок на этих шкалах.

У оппозиционной шкалы всегда есть два конца (полюса) и середина

(нейтральная точка), которая делит всю шкалу на две части –

положительную и отрицательную

--------------------------------------------------------------------------------------------

-1 0 +1

A^– A₀ A⁺

В середине шкалы происходит переключение с одного типа оценок на другой.

Требование аддитивности меры является слишком жестким

и ограничительным для многих практических задач информатики,

в частности, для процедур экспертного оценивания и

формирования мнений.

Существует гипотеза о том, что неаддитивность есть одно из

фундаментальных отличий процедур оценивания от процедур

измерения.

Тогда в качестве базы для оценивания предлагается

пространство с предмерой Г= (X, , u), где предмера u

удовлетворяет лишь условиям ограниченности и монотонности

Таким образом, произвольная псевдомера, называемая

также неклассической (неаддитивной) мерой, строится

как однопараметрическое расширение обычной меры путем

замены стандартной аксиомы аддитивности каким-либо

более общим условием.