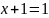Билет 1.1
Понятие логической алгебры и его использование в искусственном интеллекте. Чем логика отличается от алгебры? Алгебраические модели логической семантики.
Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается (т. н. бинарная или двоичная логика, в отличие от, например, троичной логики), что высказывания могут быть только истинными или ложными.
Алгебра логики является разделом логики.
Алгебраическое представление булевой логики в виде логической матрицы:
Использование в ИИ:
логика как основа представления знаний и формализации рассуждений
логика как инструмент исследования естественного языка
логика как язык программирования
Логика определения
Логика – это наука о человеческом мышлении, его законах и формах
Логика – это наука о правильных рассуждениях (законах, правилах и нормах корректных рассуждений)
Логика – это наука об искусственных средствах оперирования языком (А.А.Зиновьев), специальная теория искусственных языковых систем
Логика – это наука о наиболее общих законах существования истины (Г. Фреге)
Билет 1.2
Операция импликации. Виды импликаций в нечетких логиках.
Импликация (implicatio - связь) — бинарная логическая связка, по своему применению приближенная к союзам «если… то…».
Импликация записывается как посылка → следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие).
Импликация Лукашевича
|
1 |
0.5 |
0 |
1 |
1 |
0.5 |
0 |
0.5 |
1 |
1 |
0.5 |
0 |
1 |
1 |
1 |
Импликация Клини (неопределенность)
|
1 |
0.5 |
0 |
1 |
1 |
0.5 |
0 |
0.5 |
1 |
0.5 |
0.5 |
0 |
1 |
1 |
1 |
Импликация Бочвара (бессмыслица)
|
1 |
0.5 |
0 |
1 |
1 |
0.5 |
0 |
0.5 |
0.5 |
0.5 |
0.5 |
0 |
1 |
0.5 |
1 |
Импликация Гейтинга (полу-истина)
|
1 |
0.5 |
0 |
1 |
1 |
0.5 |
0 |
0.5 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Импликация Брауэра (двойственная Гейтингу)
|
1 |
0.5 |
0 |
1 |
0 |
0 |
0 |
0.5 |
1 |
0 |
0 |
0 |
1 |
0.5 |
0 |
Импликация Финна
+1 – истина
-1 – ложь
0 – противоречие
τ – неопределенность
|
+1 |
-1 |
0 |
τ |
+1 |
+1 |
-1 |
0 |
τ |
-1 |
+1 |
+1 |
+1 |
+1 |
0 |
+1 |
-1 |
+1 |
τ |
τ |
+1 |
-1 |
0 |
+1 |
Нечеткие импликации
Логика |
n |
T |
S |
I |
Z (Заде) |
1-p |
min{p; q} |
max{p; q} |
max{1-p/q} |
L (Лукасевича) |
1-p |
max{0; p+q-1} |
min{1; p+q} |
min{1; 1-p+q} |
R (Рейхенбаха) |
1-p |
p*q |
p+q-p*q |
1-p+q*p |
G (Гейтинга) |
|
min{p;q} |
max{p; q} |
|
