Неньютоновское течение

Класс приложений Non Newtonian Flow подходит для течений, в которых изменение вязкости нарастает со скоростью сдвига. Этот тип приложений почти идентичен классу Incompressible Navier-Stokes, за исключением предоставленного для удобства средств описания динамической вязкости. Оно включает специальное диалоговое окно для описания вязкости по степенному закону и в соответствии с моделью Карро, а также опцию для ввода вашей собственной зависимости.

Уравнением движения являются обычные уравнения Навье-Стокса:

где  — динамическая вязкость [M L^–1 T^–1], u – вектор скорости [L T^–1],  — плотность жидкости [M L^–3], и p — давление [M L^–1 T^–2], F —массовые силы [M L^–2 T^–2]. Выражение для вязкости может быть выбрано из модели степенного закона в соответствии с уравнением 4-30:

где m и n скаляры, которым можно присвоить любые значения, а [M L^–1 T^–1] определяется выражением:

В соотношении 4-31 и является производной от u по направлению x, что аналогично для других компонент и пространственных производных. Степенной закон может описывать жидкости как с истончением, так и с утолщением сдвига за счет показателя степени n. Для ньютоновских жидкостей значение n равно единице.

Выражение Карро задает вязкость следующим уравнением с четырьмя параметрами

где  — параметр с размерностью времени (T), 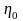— вязкость нулевой скорости сдвига и — вязкость при бесконечной скорости сдвига. Это выражение способно описать вязкость для большинства стационарных течений полимеров.

Последнее изменение в приложении Non Newtonian Flow основывается на общем выражении для динамической вязкости. Встроенная переменная или имя переменной для скорости сдвига, sr_chin, позволяет легко и быстро ввести произвольное выражение вязкости как функции скорости сдвига.

Граничные условия для приложения Non Newtonian Flow идентичны тем, которые используются в приложении Incompressible Navier-Stokes:

Приложение Non Newtonian Flow поставляется также со специального типа элементами функции формы конечных элементов. Они включают возможность обрабатывать разрывы в давлении и часто называются «пузырьковыми» элементами. Суммарная сводка их приведена в главе Реализация типов Приложений в подразделе Incompressible Navier-Stokes. Для более эффективного решения больших моделей используйте многосеточный решатель, см. раздел «Установки многосеточного решателя» на странице 133 Руководства по моделированию в COMSOL Multiphysics.

Закон Дарси для течения в пористой среде

В пористой среде общий перенос количества движения за счет сдвиговых напряжений в жидкости пренебрежимо мал, поскольку стенки поры препятствуют этому переносу за пределы отдельной поры. Детальное описание вплоть до каждой отдельной нецелесообразно в большинстве моделей, так что обычным приближением является усреднение пористой и жидкой среды в одну сплошную однородную среду. Закон Дарси основывается на таком осреднении и описывает течение в пористой среде, когда движущей силой движения является только градиент давления.

Закон Дарси утверждает, что вектор скорости определяется градиентом давления, вязкостью жидкости и структурой пористой среды.

В этом уравнении k означает проницаемость пористой среды [L²],  — динамическая вязкость [M L^–1 T^–1], u – вектор скорости [L T^–1], и p — давление [M L^–1 T^–2].

Класс приложений Darcy’s Law в модуле Chemical Engineering объединяет закон Дарси с уравнением неразрывности:

В последних уравнениях  — плотность жидкости [M L^–3] и  — объемная доля жидкости. Это приложение должно обычно связываться с законом газа и даже с энергетическим балансом, где плотность будет описываться как функция температуры и давления.

Плотность газа зависит от давления, что для идеального газа описывается законом идеального газа:

Где M означает молекулярный вес газа [M N^–1], R — газовая постоянная [M L² T^–2 N^–1 ^–1] и T — температура [].

Закон Дарси совместно с уравнением неразрывности и уравнением состояния для идеального газа составляет четкую математическую модель для широкого спектра приложений, рассматривающих течение в пористой среде. В классе Darcy’s Law вы можете совместить эти уравнения с граничным условиями для заданного давления:

граничным условием непроницаемости или симметрии;

или задать условие inflow/outflow (задать скорость) перпендикулярно границе:

На внутренних границах доступно также условие по заданному давлению.

Приведенный ниже раздел дает пример использования приложения Darcy’s Law для моделирования течения переменной плотности в пористой среде…….