Балансы количества движения

Изучение свойств течений в реакциях или рабочих устройствах основывается на математических моделях, выражающих законы сохранения количества движения и масс. Модуль Chemical Engineering реализует эти законы сохранения различными способами для классов приложений.

Для течения в пористой среде для этих законов доступны расширения Дарси и Бринкмана, которое включает вязкое слагаемое. Для ламинарного течения используются уравнения Навье-Стокса для несжимаемой жидкости и неизотермического течения. Также включено описание вращательного движения, использующее цилиндрические координаты. Неньютоновские жидкости доступны с интерфейсом для степенного закона и модели Каро для вязкости или определяемых пользователем моделей для описания вязких эффектов. Турбулентные течения реализованы в виде модели k–, а высоко скоростные течения могут моделироваться с использованием двумерной версии уравнений Эйлера для сжимаемой жидкости.

В последующих разделах представлены и коротко описаны классы приложений из модуля Chemical Engineering для течения жидкости. Описано несколько простых примеров с пошаговыми инструкциями по их выполнению, чтобы проиллюстрировать каждый из классов приложений.

Уравнения Навье-Стокса

Уравнения Навье-Стокса описывают течение вязкой жидкости посредством баланса количества движения для каждой компоненты скорости по всем пространственным измерениям. Они предполагают также, что плотность и вязкость в модели являются постоянными, что приводит к уравнению неразрывности.

Класс приложений Incompressible Navier-Stokes в модуле Chemical Engineering представляет собой нечто большее, чем классическое понимание этих уравнений, и включает в себя учет произвольных изменений вязкости и небольших вариаций плотности посредством, например, приближения Буссинеска.

Данный раздел дает суммарное описание соответствующих уравнений и граничных условий для одного наиболее привычной формулировки, используемой в математическом моделировании. Ниже показано также, как можно масштабировать уравнения Навье-Стокса.

Уравнения

Уравнения в классе приложений Navier-Stokes определяются уравнениями (4-1). Уравнения количества движения и уравнение неразрывности образуют нелинейную систему уравнений из трех или четырех уравнений для двумерного и трехмерного случаев соответственно:

где  — динамическая вязкость [M L^–1 T^–1], u – вектор скорости [L T^–1],  — плотность жидкости [M L^–3], p — давление [M L^–1 T^–2] и F — член массовых сил L^–2 T^–2].

Граничные условия могут быть в одной их описанных ниже форм. Для заданной скорости вы можете задать вектор скорости, нормальный к границе в виде:

Которое представляет собой тип граничного условия Inflow/Outflow. Вместо этого вы можете задать давление в граничном условии Outflow/Pressure:

Имеется специальное граничное условие, которое является комбинацией обоих этих описаний. Это граничное условие Normal Flow/Pressure или «прямолинейный выход», которое полагает тангенциальную компоненту скорости, равной нулю, и давление, равным заданной величине. Это приемлемо для моделирования длинных каналов, в которых предполагается, что течение стабилизировалось настолько, что скорость в тангенциальном направлении пренебрежимо мала. Применение этого условия устраняет необходимость моделировать длину канала.

Условие Slip/Symmetry устанавливает, что отсутствует компонента скорости, нормальная к границе:

Граничное условие Neutral устанавливает, что перенос касательными напряжениями вдоль границы равен нулю. Это условие называется нейтральным, поскольку оно не накладывает никаких ограничений на скорость и означает, что вдоль моделируемой границы отсутствуют какие-либо взаимодействия.

Граничное условие No slip обнуляет все компоненты вектора скорости:

Масштабирование

Многие моделируемые области могут быть большими в одном направления по сравнению с другими. Это может создавать необоснованно большие вычислительные трудности, которые могут оказаться неразрешимыми.

Масштабирование процесса идеально переводит уравнения Навье-Стокса к безразмерной форме. В этом случае, введите характерную дину, d, и характерную скорость, 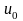, Для течение в круглой трубе, d часто является ее диаметром, а — средняя скорость. В этом случае определите безразмерные переменные в соответствии с:

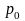где — означает давление отсчета. Уравнения количества движения в безразмерном виде принимают вид

где дифференциальные операторы также выражаются в безразмерном виде. Это означает, что граничные условия геометрия области должны быть также определены в безразмерном виде. Обратные величины выражений в квадратных скобках представляют число Рейнольдса и Фруда соответственно.

Приложение Incompressible Navier-Stokes также поставляется со специальными типами элементов. Они включают несплошной элемент (shdisc) и пузырьковый элемент (shbuble). Сводку этих элементов см. в главе Реализация классов приложений в подразделе Несжимаемые уравнения Навье-Стокса.

Чтобы решать большие модели более эффективно, используйте многосеточный решатель, см раздел «Параметры многосеточного решателя » на стр. . в Руководстве по Моделированию в модуле Multiphysics. Навигатор моделей содержит в своем дереве также специальную точку входа Steady-state analysis with multigrid в ветви Incompressible Navier-Stokes. Эта точка входа доступна в режиме 3D и устанавливает параметры решателя для решения больших моделей с многослойной сеткой.

Уравнения Навье-Стокса описывают не только все типы ньтоновских несжимаемых течений, но теоретически могут также описывать турбулентное течение. Однако моделирование турбулентного потока с помощью уравнений Навье-Стокса непрактично в большинстве инженерных приложений, поскольку разрешения очень маленьких вихрей. К тому же, течение не может быть названо стационарным, поскольку вихри в потоке движутся случайным образом.

Эти типы нестационарных моделей очень требовательны к количеству вычислительных операций и требуют много памяти, и они слишком велики для большинства компьютеров. Поэтому для моделирования турбулентного потока необходимо использовать упрощенные модели. Одним из таких приближений является k– модель турбулентности, доступная в этом модуле.