Домашняя контрольная работа по темам «Двойные, тройные интегралы» и «Комплексные числа и функции комплексного переменного»

1. Не выполнять №№ 5, 6, 9!!!!!

2. Изучить «Образец решения контрольной работы»!

Интегрирование функций многих переменных.

Вычисление двойного интеграла в декартовых координатах.

Пусть функция определена в некоторой замкнутой области D плоскости . Составим интегральную сумму для функции по области D : , разбив область D произвольно на n элементарных областей , не имеющих общих внутренних точек, где - площади этих областей, _{- значение функции в произвольной точке} области D. Предел интегральной суммы при d=max{ }→ 0 (n→∞) называется двойным интегралом по области D от функции :

. (1)

Вычисление двойного интеграла осуществляется сведением к повторному интегралу:

(2)

у

L

n

A B

а в х

рис.4

у=φ₂(х))

p

у=φ₂(х)

Рис.1

(3)

у

Q

d

x=ψ₁(y) x=ψ₂(y)

n C q

c

x

Рис 2.

Площадь S плоской области D вычисляется по формулам:

(4) S= = , если область в декартовой системе координат определена неравенствами

(5) S= = , если область в полярной системе координат определена неравенствами

Объем V цилиндрического тела, ограниченного снизу плоскостью z=0, сверху непрерывной поверхностью z=f(x,y), проекцией которой на плоскость ХОУ является область D, вычисляется по формуле V= . (6)

Вычисление тройного интеграла в декартовых координатах.

Пусть функция определена и непрерывна в пространственной области V, ограниченной сверху поверхностью , а снизу – поверхностью , где функции и определены и непрерывны в области D .

Тогда тройной интеграл вычисляется по формуле: (7) , причем при вычислении внутреннего интеграла переменные х и у считаются константами.

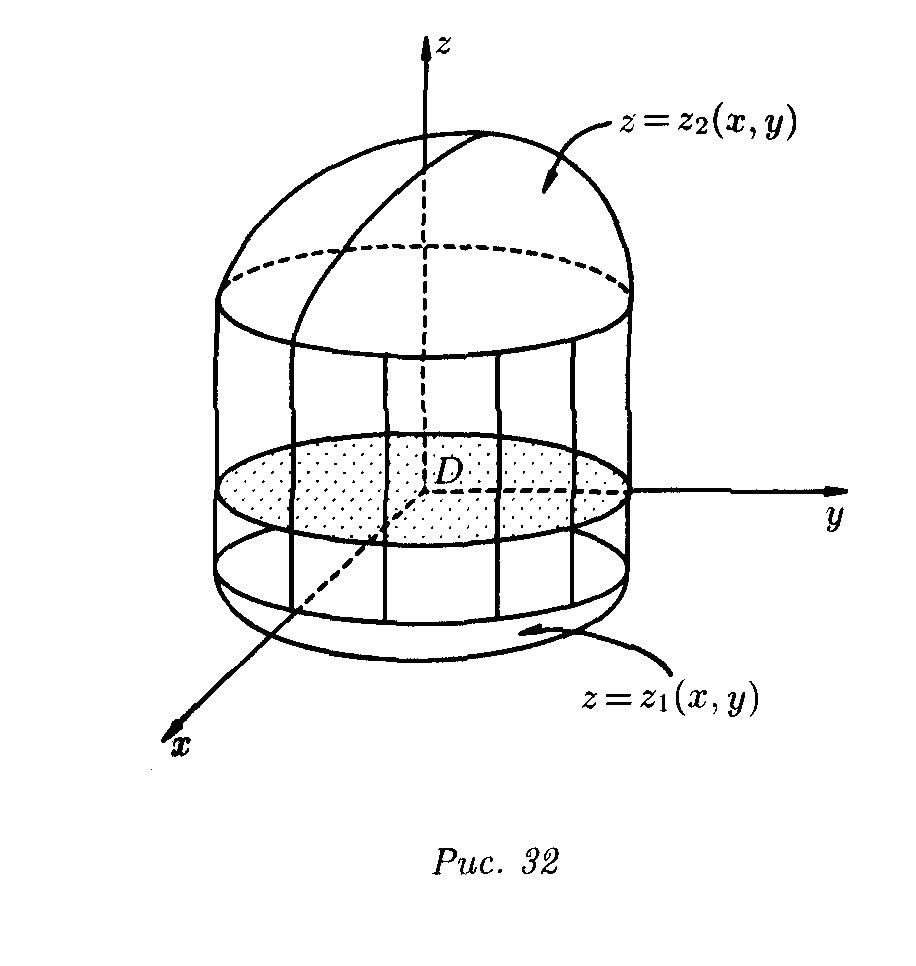
Рис.3

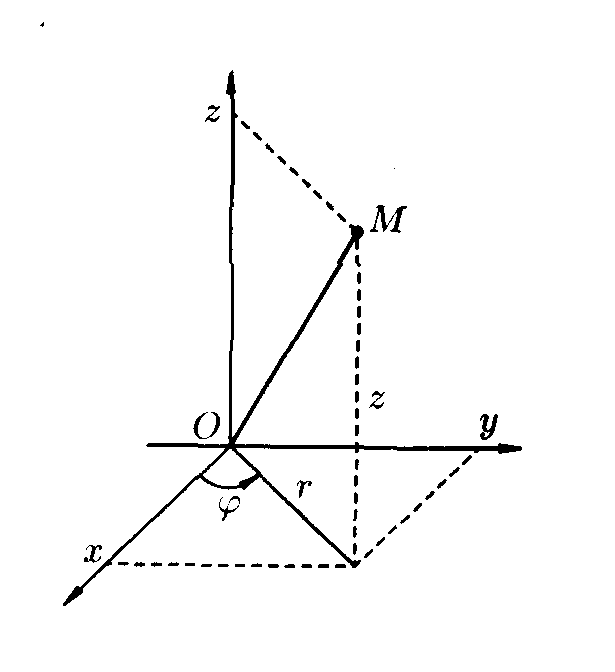
Вычисление тройного интеграла в цилиндрических координатах.

Цилиндрические координаты есть обобщение полярных координат на плоскости и связаны с прямоугольными координатами (x,y,z) формулами:

Рис. 4.

(8)

Переход к тройному интегралу в цилиндрических координатах осуществляется по формуле: (9) , где - модуль якобиана перехода от декартовых к цилиндрическим координатам.

Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случае, если тело V проецируется в круг или часть круга.

Вычисление тройного интеграла в сферических координатах.

С

Рис.5.

ферические координаты связаны с прямоугольными координатами (x,y,z) формулами:

(9)

Модуль якобиана перехода равен

Переменные в общем случае изменяются в пределах:

.

Переход к тройному интегралу в сферических координатах осуществляется по формуле:

(10) .

Определим объемную плотность распределения массы в точке P тела как предел отношения массы элементарного тела, содержащего точку P к ее объему, когда диаметр элементарного тела стремится к нулю. Тогда:

1. Объем пространственной области

. (11)

2. Масса тела, занимающего область ,

, (12)

где - плотность вещества.