3. Уравнение регрессии

В статистике выделяют различные виды регрессионные модели.

Парная регрессия - представляет собой регрессию между двумя переменными. В качестве примера можно назвать зависимость прибыли предприятия (зависимая переменная) от производительности труда (объясняющая переменная);

Множественная регрессия - регрессия между зависимой переменной у и несколькими причинно обусловленными объясняющими (независимыми, или предсказывающими) х₁ х₂,..., х_т. Так, имеется множественная регрессия между прибылью предприятия (y) и производительностью труда (x₁), объем основных фондов (x₂), объем оборотных средств (x₂).

Наиболее часто встречающиеся типы функции:

Название	Функция
Линейная
Параболическая
Гиперболическая
Показательная
Степенная

Основным методом решения задачи нахождения параметров а₀ и а₁ уравнения связи является метод наименьших квадратов (МНК), разработанный Гауссом. Он состоит в минимизации суммы квадратов отклонений фактических значений от значений, вычисленных по уравнению связи.

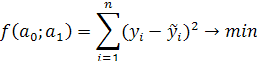
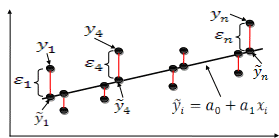
Схема 1 – Сущность метода наименьших квадратов

Для нахождения параметров а₀ и а₁ при которых принимает минимальное значение необходимо частные производные функции прировнять нулю:

Далее преобразуем полученные уравнения до выражения, которое называют системой нормальных уравнений:

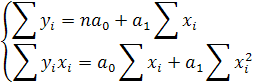
Разделим оба уравнения системы на n, получим следующее выражение:

Преобразуя предложенную систему получить следующие формулы для нахождения параметров уравнения:

Параметр уравнения a₁ также можно вычислить, используя формулу:

Преобразуя выражение получаем:

r_xy – парный линейный коэффициент корреляции между x и y;

_x, _y – стандартное отклонение.

а₀ – не имеет экономической интерпретации, но существует мнение, что он показывает усредненное влияние всех прочих факторов, не включенных в исследование.

а₁ – коэффициент регрессии, показывает, на сколько в среднем изменится величина результативного признака y при изменении факторного признака x на натуральную единицу.

Если а₁ >0 то связь прямая, если а₁ < 0 то связь обратная.

На практике для нахождения параметров множественной регрессии в связи с большим объемом расчетов прибегают к помощи ПЭВМ и специализированных пакетов программ:

Коэффициенты условно-чистой регрессии а_j являются именованными числами, выраженными в разных единицах измерения, и поэтому несравнимы друг с другом. Для преобразования их в сравнимые относительные показатели применяется следующий метод:

Стандартизованный коэффициент регрессии или  - коэффициентом:

Показывает, на сколько среднеквадратических отклонений () изменится результативный признак если величина факторного признака изменяются на одно среднеквадратическое отклонение.

Коэффициент эластичности:

Показывает на сколько процентов в среднем изменится значение зависимой переменной y если независимая переменная x изменится на 1%.