Показатели измерения множественной линейной корреляции

Важнейшим показателем интенсивности связи в многофакторной системе является множественной коэффициент детерминации, обозначаемый заглавной латинской буквой R².

Он измеряет общую тесноту связи вариации результативного признака с вариацией всей системы входящих в модель факторов. Другими словами он характеризует удельный вес (процент) общей дисперсии, ко­торый объясняется уравнением регрессии (или изменением факторного показателя х). Чем больше этот удельный вес, тем в большей степени вариация у объясняется изменениями комплекса пере­менных х, и, следовательно, связь между ними является более интенсивной.

Значение коэффициента детерминации изменяется от 0 до 1 и никак не указывает на направление связи.

Величина множественного коэффициента детерминации может быть вычислена несколькими способами:

а) на основе матрицы парных коэффициентов корреляции. При наличии линейной зависимости возможно определение R² через матрицу коэффициентов корреляции, при этом формула для расчета выглядит следующим образом:

где ’ – определитель матрицы парных коэффициентов корреляции;

 – определитель матрицы межфакторной корреляции, не включающей первой строки _r и ее последнего столбца, то есть:

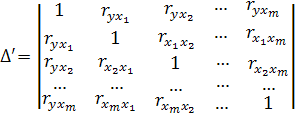
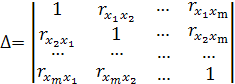
б) на основе парных коэффициентов корреляции и бета коэффициентов:

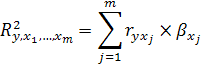
в) как корреляционное отношение, то есть отношение общей вариации (общая сумма квадратов) к вариации остатков (суммы квадратов остатков).

- выровненные значения по уравнению регрессии;

y_i - индивидуальное значение результативного признака;

- среднее значение результативного признака.

Математические свойства МНК таковы, что величина множественного коэффициента детерминации автоматически приближается к единице при числе факторов, приближающемся к n-1. При этом совершенно неважно, введены ли в модель реальные факторы, или любые варьирующие величины, не относящиеся к изучаемой проблеме. Чтобы исключить эту проблему из величины коэффициента детерминации, проводится его корректировка на потерю степеней свободы, получаемый показатель называется скорректированный коэффициент множественной детерминации:

На практике показатель используется для выявления наилучшей модели из числа возможных.

Показатели измерения частной линейной корреляции

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. В случае двух независимых переменных имеем:

;

Для применения частного коэффициента корреляции необходи­мо соблюдать следующие условия:

1. Сравниваемые переменные должны быть измерены в шкале интервалов или отношений

2. Предполагается, что все переменные имеют нормальный закон распределения

3. Число варьирующих признаков в сравниваемых переменных должно быть одинаковым

4. Для оценки уровня достоверности корреляционного отношения Пирсона следует пользоваться формулой (приведенной выше) и таблицей критических значе­ний для t-критерия Стьюдента при k = n – 2.