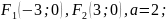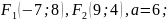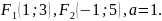§12. Гіпербола та її властивості. Канонічне рівняння гіперболи

Гіперболою називають множину точок площини, різниця відстаней від кожної з яких до двох даних точок залишається сталою і дорівнює 2a. Точки називають фокусами гіперболи.

Нехай , M (x;y)- довільна точка гіперболи. Розглянемо випадок, коли фокуси гіперболи знаходяться на осі х і початок координат є серединою відрізка 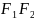. Тоді .

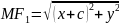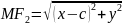, . Отже, .

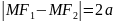Модуль взято тому, що невідомо який з відрізків 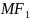чи 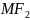буде більший.

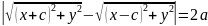
або .

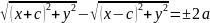Зрозуміло, що 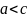, а отже .

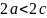Випадок, коли 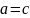розглядати не будемо, бо тоді

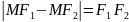- сукупність всіх точок прямої , що лежать поза межами відрізка .

+

,

,

,

,

,

,

,

,

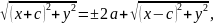
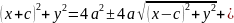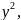
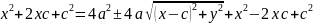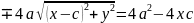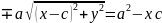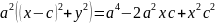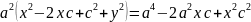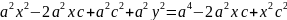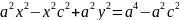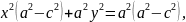
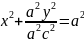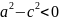, оскільки , то позначимо

.

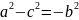Отже,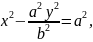

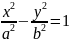- канонічне рівняння гіперболи.

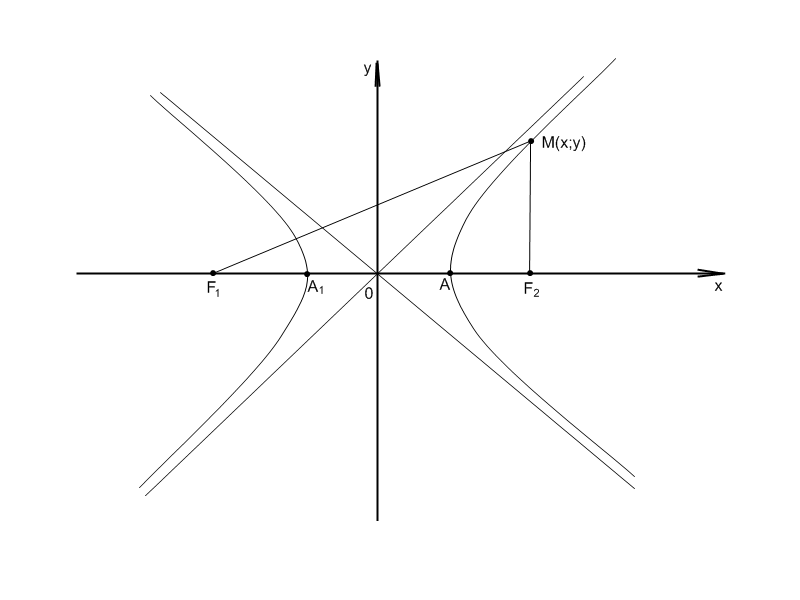
AA₁ – дійсна вісь гіперболи, - дійсна піввісь, - уявна піввісь. Так як змінні х і у входять до канонічного рівняння гіперболи у парних степенях, то гіпербола задана канонічним рівнянням, симетрична відносно обох осей координат.

Знайдемо точки, в яких вітки гіперболи перетинають вісь х, то у=0.

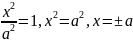, то (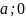 ) і (- ;0). Якщо графік перетинає вісь y, то х=0, 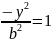або 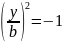. Очевидно, що ця рівність виконуватись не може. Отже, гіпербола, задана канонічним рівнянням, вісь у не перетинає. Прямі 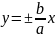- асимптоти гіперболи. Ексцентриситетом гіперболи називають = .

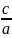Так як 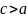, то для гіперболи

,

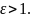
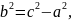
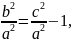
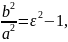
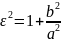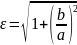або .

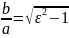Якщо 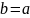, то рівняння набуває вигляду

.

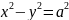Таку гіперболу називають рівносторонньою або рівнобічною. Її асимптотами є бісектриси координатних чвертей.

Прямі, задані рівняннями - називають директрисами гіперболи, заданої канонічним рівнянням . Так як .

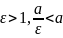Отже, директриси гіперболи не перетинають .

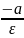
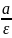
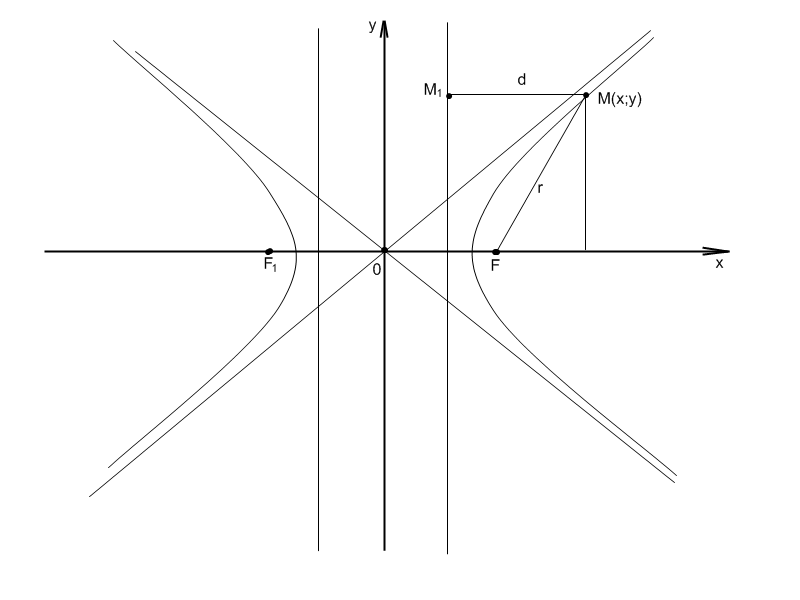
Якщо М (х;y) – довільна точка гіперболи, 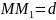- відстань до відповідної директриси, MF=r – відтань до відповідного фокусу, то .

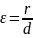Задачі для розв’язування:

1. Знайти дійсну та уявну півосі, ексцентриситет і побудувати гіперболу для всіх точок якої абсолютна величина різниці відстаней до точок стала величина, що дорівнює 2 , якщо:

1. 

2. 

3. 

2. Знайти a,b, c, та рівняння асимптот. Якщо гіперболу задано рівнянням

1. 

2. .

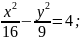
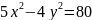3. Звести рівняння гіперболи 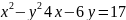до канонічного. Вказати рівняння асимптот в новій та старій системах координат.

§ 13. Парабола та її властивості. Канонічне рівняння параболи.

Параболою називають множину всіх точок площини, рівновіддалених від даної прямої та даної точки. Пряму називають директрисою параболи, а точку її фокусом. Фокус не можне лежати на директрисі.

Виведемо канонічне рівняння параболи.

Виберемо систему координат так, щоб вісь х проходила через фокус F і була перпендикулярна до директриси, а початок координат знаходився на однаковій відстані від фокуса і директриси.

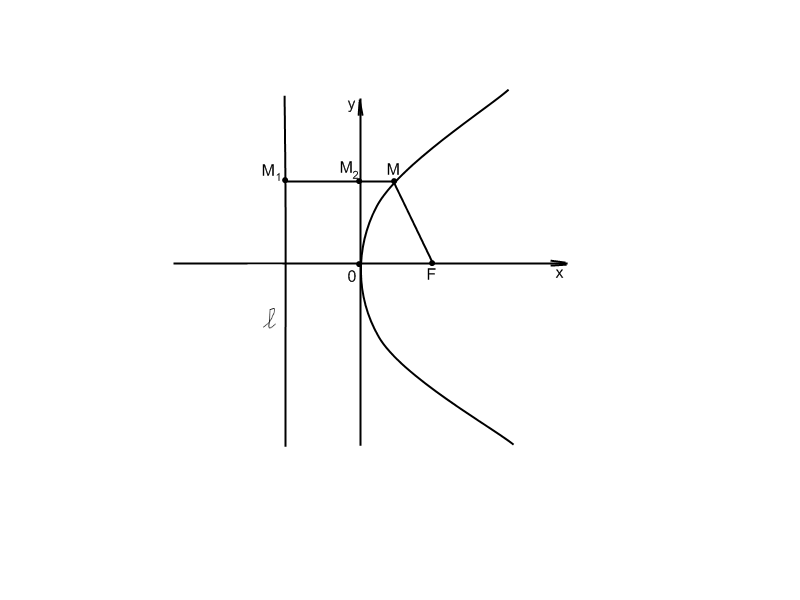
Нехай відстань від фокуса до директриси буде p – параметр параболи. Тоді F(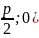 і відстань від директриси до осі у .

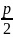Нехай M (х;y) – довільна точка параболи. MM₁ – відстань від точки M до директриси.

MM₁ = MM₂ + M₂M₁, MM₂ = х, M₂M₁= ,

то MM₁ = х+ .

M F=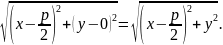

За означенням параболи M F= MM₁ .

Тоді

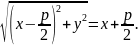
Піднісши до квадрату, одержимо

,

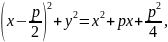
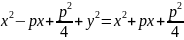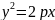- канонічне рівняння параболи.

Так як змінна у входить до канонічного рівняння параболи у парному степені, то парабола задана канонічним рівнянням, симетрична осі х. Зрозуміло, що у цьому випадку директриса параболи має рівняння .

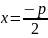Так як 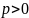, то рівняння має зміст лише при 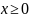, тому вітки параболи, заданої канонічним рівнянням, знаходяться у І і ІV чвертях.

Вершиною параболи називають точку перетину параболи з її віссю симетрії. У нашому випадку з віссю х. Отже, 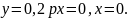Тобто вершиною параболи , заданої канонічним рівнянням, є початок координат.

Задачі для розв’язування

1. Парабола з вершиною в початку координат симетрична осі х і проходить через точку А(9;3). Напишіть її рівняння.

2. Знайти вершину й побудувати параболу, для всіх точок якої відстані до даної точки М і даної прямої 𝓁 рівні між собою, якщо рівняння прямої і координати точки задані:

1. 3х-4у-15=0; М(7;4).

2. 5х+12у - 4=0; М(1;1).

3. х+у=0, М(5;3).