
- •§1. Аксіоматична будова теорії натуральних чисел, аксіоми Пеано
- •§2. Метод математичної індукції, його застосування
- •§3. Поняття про алгебраїчні операції та алгебраїчні структури. Група, кільце, поле.
- •§ 4. Поняття комплексного числа
- •§ 5. Форми комплексного числа. Формула Ейлера. Алгебраїчна форма комплексного числа.
- •§6. Дії з комплексими числами, формула Муавра. Корінь з комплексного числа
- •§ 7. Матриці та визначники
- •§ 8. Системи лінійних алгебраїчних рівнянь. Ранг матриці, його обчислення. Критерій Кронекера- Капеллі
- •§9. Системи лінійних рівнянь. Невизначені системи. Метод Гаусса.
- •§ 10. Метод Крамера .
- •§11. Матричний метод розв’язування системи лінійних рівнянь
- •§1. Вектори. Дії з векторами. Колінеарні, компланарні вектори.
- •§ 2. Лінійно-залежні і незалежні системи векторів. Векторний базис.
- •§3. Векторний добуток векторів. Властивості, геометричний зміст
- •§4. Мішаний добуток векторів. Властивості, геометричний зміст
- •§ 5 Рівняння прямої на площині
- •§6. Основні задачі на пряму на площині.
- •§7. Рівняння площини в просторі
- •§8. Основні задачі на площину
- •§9. Рівняння прямої у просторі: перетином двох площин, через дві точки, канонічне
- •§10. Кут між прямою та площиною.
- •§11. Еліпс та його властивості. Канонічне рівняння еліпса.
- •§12. Гіпербола та її властивості. Канонічне рівняння гіперболи
- •§ 13. Парабола та її властивості. Канонічне рівняння параболи.
- •§14. Поверхні другого порядку. Класифікація
§9. Рівняння прямої у просторі: перетином двох площин, через дві точки, канонічне
Нехай маємо дві площини, задані рівняннями
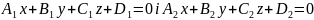 .
.
Якщо
їх нормальні вектори
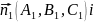
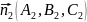 не
колінеарні, то площини перетинаються.
Як відомо дві площини можуть перетинатися
лише по прямій.
не
колінеарні, то площини перетинаються.
Як відомо дві площини можуть перетинатися
лише по прямій.
Отже,
система
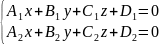
задає пряму у просторі.
Ця пряма є прямою перетину цих площин.
Систему називають загальним рівнянням прямої в просторі.
2. Канонічне рівняння прямої
Нехай
дано точку
і ненульовий вектор
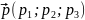 .
Потрібно скласти рівняння прямої, що
проходить через точку
, паралельно вектору
.
Нехай M
(x;y;
z)
– довільна точка цієї прямої. Тоді
вектори
.
Потрібно скласти рівняння прямої, що
проходить через точку
, паралельно вектору
.
Нехай M
(x;y;
z)
– довільна точка цієї прямої. Тоді
вектори
(x-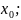 ,
y-
,
y- ;
z-
;
z-
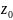 )
і вектор
- колінеарні, а отже їх відповідні
координати пропорційні. Тобто маємо
рівняння
)
і вектор
- колінеарні, а отже їх відповідні
координати пропорційні. Тобто маємо
рівняння
 .
.
Ці рівняння називають канонічними рівняннями прямої.
Зазначимо, що в цьому рівнянні деякі із знаменників можуть дорівнювати нулю. Цей нуль слід сприймати як відповідну координату вектора .
Зокрема,
якщо
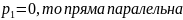 площині
площині
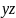 ;
якщо
;
якщо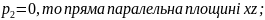 якщо
якщо
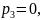 то пряма паралельна площині x
то пряма паралельна площині x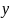 .
.
Якщо
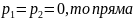 паралельна осі
.
паралельна осі
.
Якщо
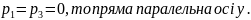
Якщо
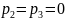 ,
то пряма паралельна осі х.
,
то пряма паралельна осі х.
3. Рівняння прямої, що проходить через дві дані точки
Складемо
рівняння прямої, що проходить через
точки
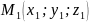 і
і
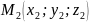 .
Нехай M(x;y;z)
- довільна точка прямої, відмінна від
точок
.
Тоді вектори
(
.
Нехай M(x;y;z)
- довільна точка прямої, відмінна від
точок
.
Тоді вектори
(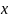 -
,
y-
-
,
y- ,
z-
)
і
,
z-
)
і
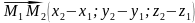 колінеарні,
оскільки належать одній прямій, а отже,
їх відповідні координати пропорційні.
колінеарні,
оскільки належать одній прямій, а отже,
їх відповідні координати пропорційні.
Отже,
 - рівняння прямої, що проходить через
дві дані точки.
- рівняння прямої, що проходить через
дві дані точки.
Зазначимо,
що в цьому випадку в знаменниках теж
можуть стояти нулі. Наприклад,
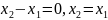 .
Це означає, що пряма паралельна площині
(перпендикулярна до осі х).
.
Це означає, що пряма паралельна площині
(перпендикулярна до осі х).
 пряма
паралельна площині
пряма
паралельна площині
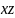 (перпендикулярна осі у).
(перпендикулярна осі у).
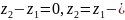 пряма
паралельна площині
пряма
паралельна площині
 (перпендикулярна
осі
).
(перпендикулярна
осі
).
4. Параметричні рівняння прямої
Скористаємося канонічним рівнянням прямої
.
Нехай кожне з цих відношень дорівнює t.
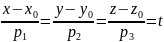 або
або
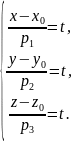
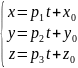 -
параметричні
рівняння прямої, t-
параметр.
-
параметричні
рівняння прямої, t-
параметр.
5. Кут між прямими
Нехай задано дві прямі
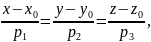
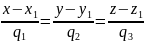 .
.
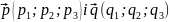 -
їх напрямні вектори. Кут між цими прямими
знайдемо як кут між їх напрямними
векторами.
-
їх напрямні вектори. Кут між цими прямими
знайдемо як кут між їх напрямними
векторами.
Для цього скористаємося скалярними добутком векторів.
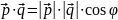 ,
- кут між векторами
,
- кут між векторами
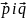 ,
тоді
,
тоді
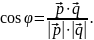
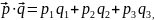
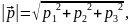
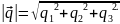
Отже,
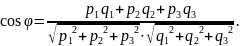
Якщо , то знайдений кут є кутом між прямими.
Якщо , то щоб знайти кут між прямими потрібно змінити знак знайденого виразу.
Якщо
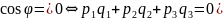 ,
то прямі перпендикулярні.
,
то прямі перпендикулярні.
Задачі для розв’язування:
Знайти рівняння прямої у кожному з таких випадків:
пряма проходить через початок координат і паралельна прямій, яка проходить через точки
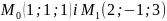 ;
;пряма перпендикулярна площині о і проходить через точки
 ;
;пряма паралельна осі ох і проходить через точку
 ;
;пряма проходить через точку
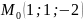 і паралельна площинам оху і о
.
і паралельна площинам оху і о
.
Знайти канонічне рівняння прямої в кожному з випадків:
пряма проходить через точку
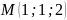 паралельно прямій
паралельно прямій
 ;
;пряма належить площині
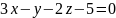 ,
перетинає пряму
,
перетинає пряму
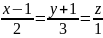 і
перпендикулярна до цієї прямої;
і
перпендикулярна до цієї прямої;
пряма проходить через точку
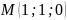 паралельна площині
паралельна площині
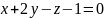 і
перетинає пряму
і
перетинає пряму
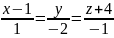 .
.
Знайти відстань від точки
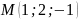 до даної прямої
до даної прямої
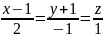 .
.
