§8. Основні задачі на площину

1. Вектор нормалі до площини. Нормальне рівняння площини

Нормальною прямою до площини називають будь-яку пряму, перпендикулярну до цієї площини. Нормаллю до площини будемо називати вектор, перпендикулярний до даної площини.

Нехай вектор – нормальний вектор площини.

Пронормувавши вектор 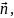одержимо вектор

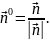
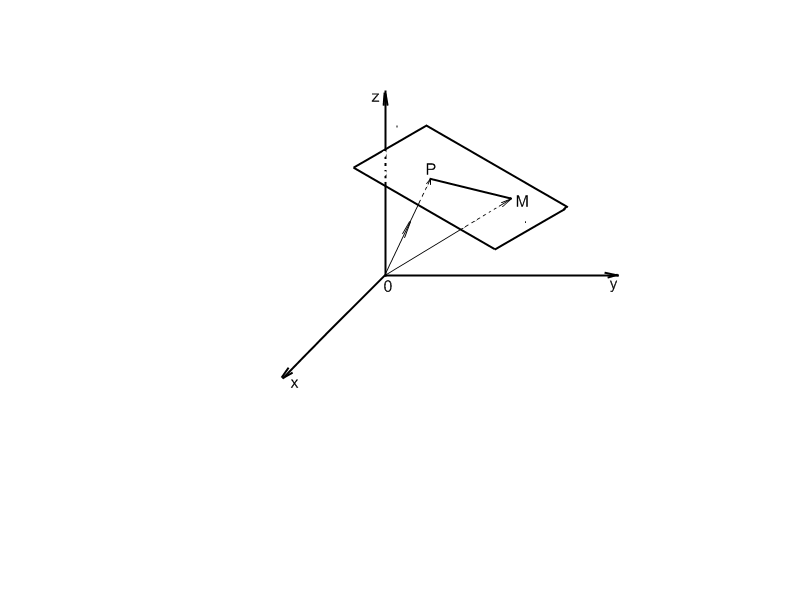
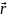
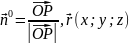-радіус-вектор довільної точки площини.

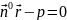–нормальне рівняння площини у векторній формі,

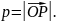
Запишемо це рівняння у координатній формі.

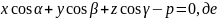
- кут , який утворює вектор з віссю х,

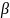- кут, який утворює вектор з віссю у,

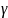- кут, який утворює вектор з віссю z.

- називають напрямними косинусами.

Щоб одержати нормальне рівняння площини із загального Ах+Ву+Cz+D=0, достатньо його поділити на 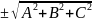, причому знак «+» або «-» слід обрати протилежний до знаку параметра D. Зазначимо, що завжди буде правильною рівність

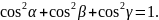
2. Відстань від точки до площини

Знайти відстань від точк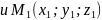 до площини, заданої рівнянням Ах+Ву+Cz+D=0 .

Нехай М(x;y;z) - довільна точка даної площини. Розглянемо спочатку випадок, коли вектори

і утворюють гострий кут.

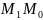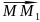Відстань від точки до площини - це відрізок . Кут між векторами і дорівнює . Тоді з

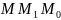 за співвідношенням

.

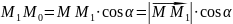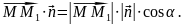
Звідси

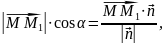
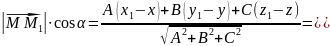
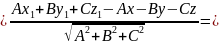
Враховуючи, що , одержимо

.

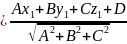Отже, .

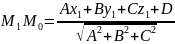У розглянутому випадку чисельник дробу додатній, оскільки кут між векторами 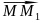і - гострий. Якщо ж кут буде тупим, то вираз, що стоїть в чисельнику, слід взяти по модулю.

Отже, відстань від точки 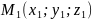до площини Ах+Ву+Cz+D = 0 обчислюється за формулою h= .

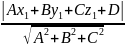3. Кут між площинами

Кутом між площинами називається будь-який з двогранних кутів, утворених цими площинами. Цей кут дорівнює куту між нормальними векторами цих площин .

Нехай маємо дві площини і

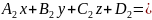0.

Тоді .

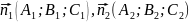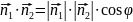, - кут між нормальними векторами, а отже й кут між площинами.

,

,

.

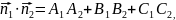
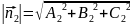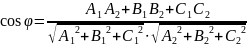Якщо 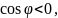це означає, що знайдено тупий кут. Для того, щоб знайти гострий кут, достатньо змінити знак, зокрема, якщо площини перпендикулярні, то вектори теж перпендикулярні , а тому

, тобто

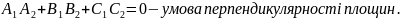
Якщо площини паралельні, то вектори - колінеарні.

Отже, 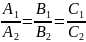- умова паралельності площин.

Задачі для розв’язування:

1. Записати нормальне рівняння площини, що проходить через точки А(1;2;3), В(1;-2;4), С(-3;5;7).

2. Знайти відстань від точки К(-1;-3;-5) до площини, що проходить через три точки А( 1;2;3), В(-1;4;5), С(2;-4;6).

3. Знайти відстань від точки К(3;4;5) до площини, яка проходить через точку А(2;-3;6) паралельно векторам .

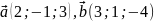4. Знайти кут між площинами 2х-3у+3z-1=0

і -2x+3y-3z+5=0.

5. Дано точки А(3;4;5), В(-2;1;7), С (2;3;-5),

D (1;2;-8).

1. Знайти кут між площинами (АВС) і( АDС);

2. Відстань від точки D до площини (АВС);

3. Відстань від точки В до площини ( АDС).