- •§1. Аксіоматична будова теорії натуральних чисел, аксіоми Пеано
- •§2. Метод математичної індукції, його застосування
- •§3. Поняття про алгебраїчні операції та алгебраїчні структури. Група, кільце, поле.
- •§ 4. Поняття комплексного числа
- •§ 5. Форми комплексного числа. Формула Ейлера. Алгебраїчна форма комплексного числа.
- •§6. Дії з комплексими числами, формула Муавра. Корінь з комплексного числа
- •§ 7. Матриці та визначники
- •§ 8. Системи лінійних алгебраїчних рівнянь. Ранг матриці, його обчислення. Критерій Кронекера- Капеллі
- •§9. Системи лінійних рівнянь. Невизначені системи. Метод Гаусса.
- •§ 10. Метод Крамера .
- •§11. Матричний метод розв’язування системи лінійних рівнянь
- •§1. Вектори. Дії з векторами. Колінеарні, компланарні вектори.
- •§ 2. Лінійно-залежні і незалежні системи векторів. Векторний базис.
- •§3. Векторний добуток векторів. Властивості, геометричний зміст
- •§4. Мішаний добуток векторів. Властивості, геометричний зміст
- •§ 5 Рівняння прямої на площині
- •§6. Основні задачі на пряму на площині.
- •§7. Рівняння площини в просторі
- •§8. Основні задачі на площину
- •§9. Рівняння прямої у просторі: перетином двох площин, через дві точки, канонічне
- •§10. Кут між прямою та площиною.
- •§11. Еліпс та його властивості. Канонічне рівняння еліпса.
- •§12. Гіпербола та її властивості. Канонічне рівняння гіперболи
- •§ 13. Парабола та її властивості. Канонічне рівняння параболи.
- •§14. Поверхні другого порядку. Класифікація
§7. Рівняння площини в просторі
Рівняння площини, що проходить через дану точку, перпендикулярно до заданого вектора
Зазначимо, що рівняння f(x,y,z)=0 визначає в просторі деяку поверхню, тобто множину всіх точок простору, координати яких задовольняють це рівняння.
Рівняння f(x,y,z)=0 називають рівнянням цієї поверхні.
Нехай
маємо точку
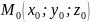 і
деякий вектор
і
деякий вектор
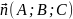 ,
причому
,
причому
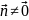 .
.
Складемо
рівняння площини, яка проходить
через
точку
і перпендикулярна до вектора
. Нехай точка
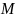 (x;y;z)
– довільна точка цієї площини. Тоді
вектор
(x;y;z)
– довільна точка цієї площини. Тоді
вектор
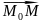 (x-
(x-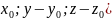 буде перпендикулярним до вектора
,
отже, їх скалярний добуток дорівнюватиме
нулю.
буде перпендикулярним до вектора
,
отже, їх скалярний добуток дорівнюватиме
нулю.
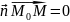
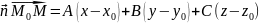 .
.
Одержимо
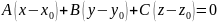 - шукане рівняння площини.
- шукане рівняння площини.
Отже, рівняння площини, що проходить через точку перпендикулярно до вектора має вигляд
.
Загальне рівняння площини
Розкривши дужки у рівнянні , одержимо
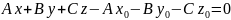 .
.
Позначивши
число
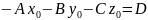 ,
одержимо
,
одержимо
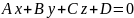 -
загальне рівняння площини.
-
загальне рівняння площини.
У цьому рівнянні - нормальний вектор даної площини.
Покажемо, що будь-яке рівняння виду є рівнянням площини.
У
цьому рівнянні принаймні один з
коефіцієнтів
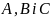 не дорівнює нулю.
не дорівнює нулю.
Нехай С≠0, тоді одержимо
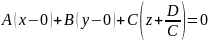 .
.
Одержали
рівняння площини з нормальним вектором
,
що проходить через точку
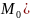 )
, що й треба було довести.
)
, що й треба було довести.
Отже, будь-яке рівняння виду задає площину.
Неповне рівняння площини
Рівняння
площини називають неповним, якщо хоча
б один з коефіцієнтів
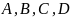 дорівнює нулю. Розглянемо можливі
випадки:
дорівнює нулю. Розглянемо можливі
випадки:
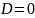 .
Одержимо рівняння
.
Одержимо рівняння
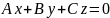 .
Очевидно, що координати точки О(0;0;0)
задовольняють це рівняння.
.
Очевидно, що координати точки О(0;0;0)
задовольняють це рівняння.
Отже, - це рівняння площини, що проходить через початок координат.
А=0. Одержимо рівняння
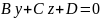 .
У цьому випадку вектор
.
У цьому випадку вектор
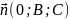 .
Вектор
.
Вектор
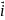 (1;0;0)
– одиничний вектор осі ox.
(1;0;0)
– одиничний вектор осі ox.
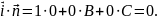
Отже, вектор перпендикулярний осі х, а тому площина задана рівнянням паралельна осі х.
В=0. Тоді

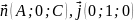 -
одиничний вектор осі y.
-
одиничний вектор осі y.
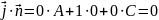 .
.
Отже,
 ,
тому площина задана рівнянням
,
тому площина задана рівнянням
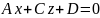 паралельна осі у.
паралельна осі у.
С=0, тоді
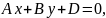
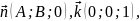
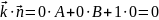 ,
то
,
то
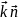 .
.
А отже, площина задана рівнянням паралельна осі z.
А=0, В=0, то
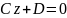 або z=
-
або z=
-
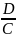 .
Ця площина паралельна одночасно осі
х і осі у, а отже
- рівняння площини, паралельної площині
ху. Зокрема, якщо D=0, одержимо Cz=0,
z=0- рівняння площини xy.
.
Ця площина паралельна одночасно осі
х і осі у, а отже
- рівняння площини, паралельної площині
ху. Зокрема, якщо D=0, одержимо Cz=0,
z=0- рівняння площини xy.А=0, С=0. Тоді
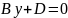 або y=
-
або y=
-
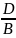 .
.
Ця
площина паралельна осі х і осі z.
Отже,
- рівняння площини, паралельної площині
хz.
Зокрема, при
,
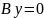 ,
у=0 – рівняння площини хz.
,
у=0 – рівняння площини хz.
7)В=0,
С=0. Тоді
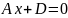 .
Ця площина паралельна осі у і осі z,
а отже, паралельна площині уz,
тому рівняння
задає площину, паралельну площині уz.
Зокрема при
,
одержимо
.
Ця площина паралельна осі у і осі z,
а отже, паралельна площині уz,
тому рівняння
задає площину, паралельну площині уz.
Зокрема при
,
одержимо
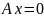 ,
х=0- рівняння площини уz.
,
х=0- рівняння площини уz.
8)А=0,
.
У цьому випадку одержимо рівняння
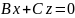 .
Ця площина проходить через точку (0;0) і
її нормальний вектор перпендикулярний
вектору
.
Отже, це рівняння площини, що містить
вісь х.
.
Ця площина проходить через точку (0;0) і
її нормальний вектор перпендикулярний
вектору
.
Отже, це рівняння площини, що містить
вісь х.
9)В=0,
.
 - рівняння площини, що містить вісь у,
бо її нормальний вектор перпендикулярний
вектору
- рівняння площини, що містить вісь у,
бо її нормальний вектор перпендикулярний
вектору
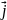 і вона проходить через точку (0;0;0).
і вона проходить через точку (0;0;0).
10)С=0,
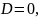
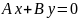 .
Нормальний вектор цієї площини
перпендикулярний вектору
.
Нормальний вектор цієї площини
перпендикулярний вектору
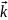 і площина проходить через точку О(0;0;0)
. Тому це рівняння задає площину, що
містить вісь
і площина проходить через точку О(0;0;0)
. Тому це рівняння задає площину, що
містить вісь
 .
.
Рівняння площини у відрізках
Скористаємося загальним рівнянням площини.
Якщо
А≠0, В≠0, С≠0, D≠0,
то
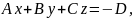
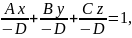

Позначивши
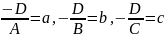 ,одержимо
,одержимо
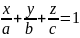 – рівняння
площини у відрізках. Тут a,
b,c
–
відрізки, які відтинає площина на осях
координат.
– рівняння
площини у відрізках. Тут a,
b,c
–
відрізки, які відтинає площина на осях
координат.
Рівняння площини, що проходить через три дані точки
 .
.
Нехай
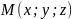 - довільна точка цієї площини. Тоді
вектори
- довільна точка цієї площини. Тоді
вектори
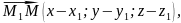
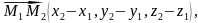
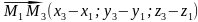 -
компланарні , а отже, їх мішаний добуток
дорівнює нулю, тому рівняння площини
можна записати у вигляді
-
компланарні , а отже, їх мішаний добуток
дорівнює нулю, тому рівняння площини
можна записати у вигляді
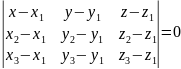
Рівняння площини, що проходить через точку паралельно двом заданим векторам
Запишемо
рівняння площини, що проходить через
точку
паралельно векторам
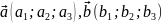 .
Нехай M(x;y;z)-
довільна точка цієї площини. Тоді
вектори
.
Нехай M(x;y;z)-
довільна точка цієї площини. Тоді
вектори
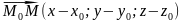 ,
- компланарні, а тому їх мішаний добуток
дорівнює нулю.
,
- компланарні, а тому їх мішаний добуток
дорівнює нулю.
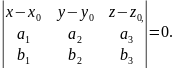
Рівняння площини,що проходить через дві точки паралельно даному вектору
Нехай
площина проходить через точку
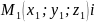
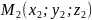 паралельно вектору
паралельно вектору
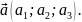 M(x;y;z)-
довільна точка цієї площини. Тоді
вектори
M(x;y;z)-
довільна точка цієї площини. Тоді
вектори
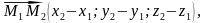 -
компланарні.
-
компланарні.
А отже, їх мішаний добуток дорівнює нулю.
Тому
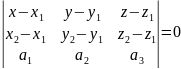 .
.
Задачі для розв’язування:
Знайти рівняння площини, яка:
1)паралельна осі у і проходить через точки М (2; -1; 2) і N(-4; 3; 7);
2)паралельна осі z і проходить через точки А((1; 2; 3) і В(-4; 3; 5);
3)паралельна осі х і проходить через точки А(1; -4; 5), В(2; -3; 1).
Знайти рівняння площини, яка проходить:
1)через вісь х і точку А(1; 3; 7);
2)через вісь y і точку В(2; 3; 4);
3)через вісь z і точку С (1; -2; 3).
Знайти рівняння площини, яка перпендикулярна вектору
 N(1;
-2; 2).
N(1;
-2; 2).Знайти рівняння площини, що проходить через точки:
А(2; 0; 0), В( 0; 5; 0), С(0; 0; 7);
А(-2;0;0), В(0; -8; 0), С(0; 0; 2);
А(7; 0; 0), В(0; -1; 0), С(0; 0; 2).
Знайти рівняння площини, що проходить через три точки:
А(1; 2; 3), В(5; -1; 2), С( 0; -5; -4), С(0; -5; -4).
А(-1; 3; 7), В(3; -2; 8), С(3; 4; -5).
Знайти рівняння площини, яка проходить через точки А(1; 2; 3), В(-3; 5; 7) паралельно вектору
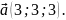
Знайти рівняння площини, яка проходить через точку М(1; 2; 3) паралельно вектору