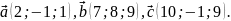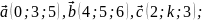§4. Мішаний добуток векторів. Властивості, геометричний зміст

Мішаним добутком трьох векторів називається число, яке дорівнює векторному добутку помноженому скалярно на вектор .

Мішаний добуток позначають .

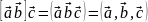Мішаний добуток володіє такими властивостями:

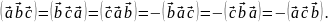
Колова перестановка трьох множників мішаного добутку не змінює його значення; перестановка двох сусідніх множників змінює знак добутку.

Мішаний добуток суми векторів на два інших вектори дорівнює сумі мішаних добутків кожного з векторів – доданків на два інших вектори.

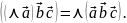
Скалярний множник можна виносити за знак мішаного добутку.

Знаючи координати векторів, можна обчислити їх мішаний добуток.

Якщо

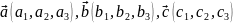
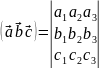
З’ясуємо геометричний зміст мішаного добутку векторів.

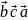
Мішаний добуток – це є число, що виражає об’єм паралелепіпеда, побудованого на векторах 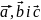, взятого із знаком плюс, якщо трійка права, із знаком мінус, якщо ця трійка ліва.

Отже, три вектори компланарні тоді і тільки тоді, коли їх мішаний добуток дорівнює нулю.

Використовуючи мішаний добуток векторів, можна обчислювати об’єм паралелепіпеда, побудованого на цих векторах.

Об’єм паралелепіпеда, побудованого на векторах дорівнює модулю мішаного добутку цих векторів.

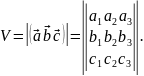
Якщо потрібно обчислити об’єм трикутної призми, побудованої на векторах , то зрозуміло, що об’єм такої призми дорівнює половині об’єму відповідного паралепіпеда. У цьому випадку

.

Так як об’єм піраміди дорівнює 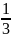об’єму паралелепіпеда, при умові, що їх основи співпадають і висоти однакові, то об’єм чотирикутної піраміди, побудованої на векторах , які мають спільний початок

,

а об’єм трикутної піраміди .

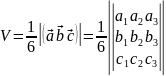Наприклад, маємо точки А(1; 2; 3), В (-3; 4; 5), С(1; -2; 3), D(3; 4; -5). Знайти :

1. об’єм паралелепіпеда, побудованого на векторах , ;

2. об’єм трикутної призми, побудованої на векторах , ;

3. об’єм чотирикутної піраміди, побудованої на векторах , ;

4. об’єм трикутної піраміди, побудованої на векторах , ;

Знайдемо координати векторів , .

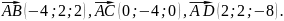
1. Знайдемо об’єм паралепіпеда:

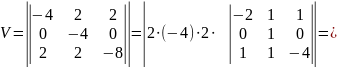
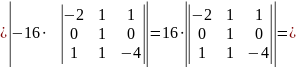
кубічних одиниць

2. Знайдемо об’єм трикутної призми.

куб. од.

3. Знайдемо об’єм чотирикутної призми.

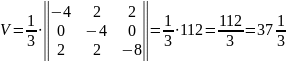куб. од.

4. Знайдемо об’єм трикутної піраміди.

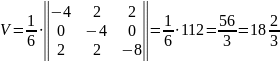куб. од.

Задачі для розв’язування:

1. Знайти мішаний добуток векторів:

1. 

2. 

2. При якому значенні k вектори будуть компланарними?

1. 

2. 

3. Дано точки А(1; 2;5), В(-1;3;8), С(2;-5;7), (3; 9; -2). Знайти:

1. об’єм паралелепіпеда, побудованого на векторах , ;

2. об’єм трикутної призми, побудованої на векторах ;

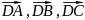3. об’єм чотирикутної піраміди, побудованої на векторах ;

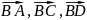4. об’єм трикутної піраміди, побудованої на векторах .

§ 5 Рівняння прямої на площині

1. Рівняння прямої з кутовим коефіцієнтом

Розглянемо пряму не паралельну осі y. Нехай ця пряма перетинає вісь y в точці B(0;b) і утворює кут з додатнім напрямом осі х. Кут відраховується від осі х проти годинникової стрілки і називається кутом нахилу прямої .

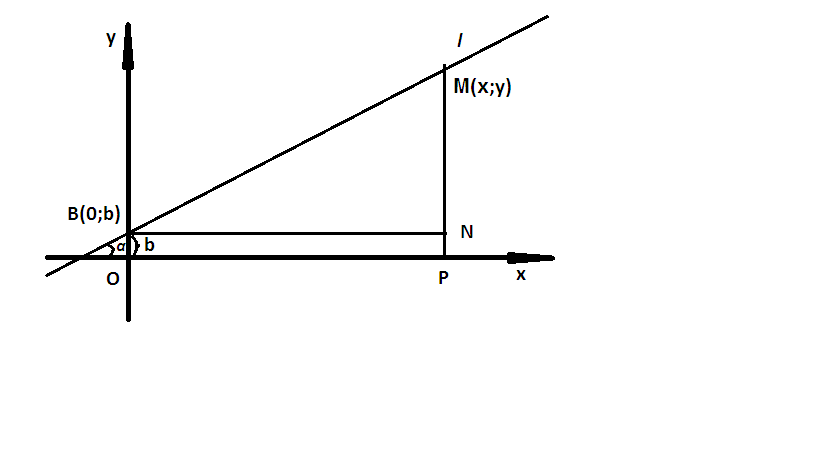
Виведемо рівняння прямої 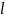. Нехай М(х; у) – довільна точка прямої . З прямокутного трикутника BMN за співвідношенням маємо

Врахувавши, що одержимо

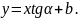
Позначивши

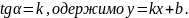
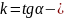кутовий коефіцієнт. Якщо 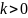,то пряма утворює з додатнім напрямом осі х гострий кут.

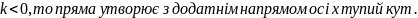
Якщо

Якщо 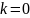, то пряма горизонтальна.

Рівняння 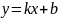- рівняння прямої з кутовим коефіцієнтом. Зокрема, якщо 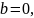то пряма проходить через початок координат. Залежно від коефіцієнтів 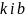пряма може розташовуватись дев’ятьма різними способами.

Пропонуємо дослідити це питання самостійно.

2. Загальне рівняння прямої

У попередньому пункті було зазначено, що рівнянням з кутовим коефіцієнтом може бути задана будь-яка не вертикальна пряма.

Загальним рівнянням може бути задана будь-яка пряма на площині.

Теорема.

Будь-яка пряма на площині у прямокутній системі координат може бути задана рівнянням 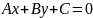і навпаки будь-яке рівняння задає деяку пряму на площині при умові, що А і В одночасно не дорівнюють нулю.

Доведення

Нехай маємо пряму, не паралельну осі у. Тоді її можна задати рівнянням

.

Отже,

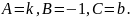
Якщо ж пряма паралельна осі у, то її рівняння матиме вигляд

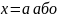
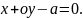У цьому випадку

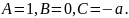
Отже, будь-яку пряму площини можна задати рівнянням .

Доведемо, що будь-яке рівняння задає деяку пряму на площині.

1. Якщо

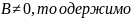
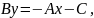
Позначивши 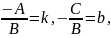одержимо рівняння - рівняння прямої з кутовим коефіцієнтом.

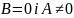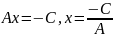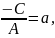2. Якщо , то одержимо рівняння . Позначивши одержимо

Рівняння , де А і В одночасно не рівні нулю, називають загальним рівнянням прямої на площині.

Зазначимо, що вектор - нормальний вектор даної прямої (вектор перпендикулярний до прямої).

3.Рівняння прямої у відрізках

Нехай у рівнянні жоден з коофіціентів не дорівнює нулю, тоді

.

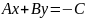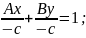
Позначивши, 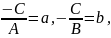одержимо 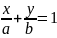- рівняння прямої у відрізках.

– відрізки, які відтинає пряма на осях координат, причому знак цих чисел вказує по який бік від початку координат знаходиться відітнутий відрізок на осі.

4.Рівняння прямої, що проходить через дві дані точки

Виведемо рівняння прямої, що проходить через точку 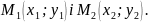Скористаємося для цього загальним рівнянням прямої: .

Так як пряма проходить через точки 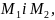то їх координати задовольняють рівняння

Тому

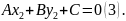
Віднявши від рівняння (1) рівняння (2), одержимо

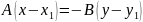або (4).

Віднявши від рівняння (3) рівняння (2), одержимо

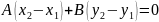або

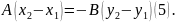
Поділивши почленно рівняння (4) на рівняння (5), одержимо

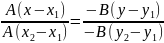або 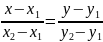– рівняння прямої, що проходить через дві дані точки.

Зазначимо, що в цьому рівнянні у знаменнику дробу може стояти нуль.

1. ; . Це означає, що пряма вертикальна;

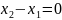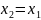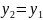2. ; . Це означає що пряма горизонтальна.

5. Рівняння прямої, що проходить через дану точку у даному напрямі

Скористаємося рівнянням прямої з кутовим коефіцієнтом Зрозуміло, що за напрям прямої відповідає кутовий коефіцієнт k, оскільки він дорівнює тангенсу кута, який утворює дана пряма з додатнім напрямом осі х.

Нехай ця пряма проходить через точку 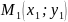. Тоді її координати задовольняють рівняння прямої. Отже, 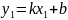. Почленно віднявши рівності одержимо

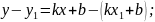
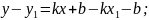
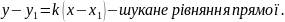
6. Канонічне рівняння прямої

Запишемо рівняння прямої , що проходить через точки

.

Зрозуміло, що 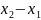і – деякі числа. Можливо одне з них дорівнює нулю (обидва не можуть дорівнювати нулю, оскільки точки 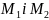- різні).

Позначимо ,

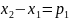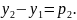
Вектор 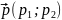називають напрямним вектором прямої.

Рівняння 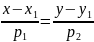- називають канонічним рівнянням прямої.

Якщо 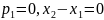, , то пряма паралельна осі у.

Якщо 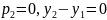, , то пряма горизонтальна.

7. Параметричне рівняння прямої

Скористаємося рівнянням

Нехай , тоді

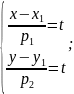
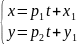- параметричне рівняння прямої, де t – параметр.

Задачі для розв’язування

1. рівняння прямої, яка утворює з додатнім напрямом очі х кут і проходить через точку А(3;7). Подати одержане рівняння у загальному вигляді та як рівняння прямої, що проходить через точку в даному напрямку, та подати його у параметричному вигляді.

2. аписати рівняння прямої, що проходить через точки

1. А(0;5), В(3;6) ; 2)А(-1;7), В(5;-4). Подати одержане рівняння у кожному з відомих вам видів.

3. аписати рівняння прямої, що проходить через точки А(-5;8), В(4;2). Знайти площу трикутника, який утворює дана пряма з осями координат.

4. Записати рівняння прямої з нормальним вектором 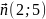, якщо ця пряма проходить через точку K(7;8).

5. Записати рівняння прямої, для якої є напрямним при умові, що пряма проходить через точку D(-1;-3).

6. Пряма задана рівнянням .

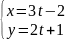Записати рівняння цієї прямої у відрізках та вказати координати напрямного вектора.

7. Трикутник ABC заданий вершинами A(-1;2), B(1;3), C(2;-5). Записати :

1. рівняння його сторін;

2. рівняння його медіан;

3. рівняння його висот .